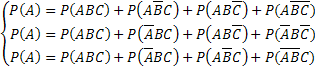Вероятность ошибки прибора

ответы

ваш ответ

похожие темы

похожие вопросы 5

Вероятность
попадания при одном выстреле для первого
стрелка равна
,
значит вероятность промаха –
.
Для второго –
,
а промаха –
.
Потому вероятность того, что при одном
залпе в мишень попадет только один из
стрелков
.

#52

Вероятность одного попадания в цель
при одном залпе из двух орудий равна
0,38. Найти вероятность поражения цели
при одном выстреле первым из орудий,
если известно, что для второго орудия
эта вероятность равна 0,8.

Решение:
Из данных задачи следует, что PA2=0,8;
PB1+B2=0,38; где
A1 и A2 –
события попадания в цель первого и
второго орудия соответственно. B1и
B2 — попадание только одного
из соответствующих орудий, т.е. B1
= A1*A2 и B2
= A2*A1 .
Обозначим как PA1=p.
Так как PB1+B2=PB1+
PB2, то подставляя, получим:

0,38=0,8-0,8p+0,2p.

p=0,7;

Вероятность поражения цели при одном
выстреле первым из орудий составляет
– 0,7.

#53

Обозначим
за

событие, что изделие 1 — стандартно

Обозначим
за

событие, что изделие 2 — стандартно

Событие Ā1 означает, что изделие 1 —
нестандартно

Событие Ā2 означает, что изделие 2 —
нестандартно

Тогда по теореме умножения вероятностей
получаем, что вероятность того, что
первое изделие стандартно, а второе –
нет, равна 0,09

(=
P(*Ā2)=P()*P(Ā2)=0.9*0.1=0.09)

Соответственно вероятность обратного
события (изделие 2 – стандартно, а изделие
1 — нестандартно) такая же

(=
P*Ā1)=P()*P(Ā1)=0.9*0.1=0.09)

Тогда по теореме сложения вероятностей
несовместных событий получаем, что
вероятность того, что одно изделие
стандартно, а другое – нет, равна 0,18

(P((*Ā2)+*Ā1))=
P(*Ā2)+
P*Ā1)=+=0.09+0.09=0.18)

Ответ:0,18

#54

Вероятность того, что при одном измерении
некоторой физической величины будет
допущена ошибка, превышающая заданную
точность равна 0,4. Произведены три
независимых измерения. Найти вероятность
того, что только в одном из них допущенная
ошибка превысит точность.

Решение:

Обозначим допущение ошибки, превышающей
заданную точность, в измерениях 1,2 и 3
как А1, А2 и А3 соответственно. Так как
эти события независимы, то по теореме
умножения вероятностей независимых
событий искомая вероятность будет
вычисляться по формуле:

Ответ: 0,432.

#55

Из партии изделий товаровед отбирает
изделия высшего сорта. Вероятность
того, что наудачу взятое изделие окажется
высшего сорта, равна 0,8. Найти вероятность
того, что из трех проверенных изделий
только два изделия высшего сорта.

Решение: Обозначим появления товаров
высшего сорта 1, 2 и 3 как А1, А2 и А3
соответственно. Так как эти события
независимы, то по теореме умножения
вероятностей независимых событий
искомая вероятность будет вычисляться
по формуле:

Ответ: 0,384.

#56

Устройство
состоит из трех элементов, работающих
независимо. Вероятности безотказной
работы (за время t) первого,
второго и третьего элементов соответственно
равны 0,6; 0,7; 0,8. Найти вероятности того,
что за время работы t
безотказно будут работать:

А) только один элемент;

Б) только два элемента;

В) все три элемента.

Решение.

Введем
обозначение событий: безотказно работало
первое устройство — A1;
безотказно работало второе устройство
— А2; безотказно работало третье устройство
— A3.

B1
– безотказно работала за время t
первое устройство A1; B2
– безотказно работало за время t
второе устройство А2; B3
– безотказно работало за время t
третье устройство A3.

а)
Появление события B1
равносильно появлению события A1;

равносильно появлению события A2
;

равносильно появлению A3
.

Таким
образом, чтобы найти вероятность
появления только одного из событий
,

достаточно найти вероятность появления
одного, безразлично какого, из событий

,

и
.
События
,

и
несовместы,
поэтому применима теорема сложения:

P
()
= P()+
P()+
P().
(*)

Остается
найти вероятности каждого из событий,

и
.
События
,

независимы, поэтому применима теорема
умножения:

P
()
=P (A1)
=;

P
()
=P (A2)
=;

P
()
=P (A3)
=.

Подставив
эти вероятности в соотношение (*), найдем
искомую вероятность появления только
одного из событий
,

:

P
()
=+

Б)
Появление события B1
равносильно появлению события A1;

равносильно появлению события A1
;

равносильно появлению A3
.

Аналогично предыдущему решению:

P
()
=+0,6*0,7*0,2+0,6*0,3*0,8+0,4*0,7*0,8=0,452.

В)
Пусть
—
безотказная работа всех устройств.
Тогда событие B равносильно
появлению
,
поэтому P(B)=P()==0,6*0,7*0,8=0,336.

#57

Вероятности того, что нужная сборщику
деталь находится в первом, втором,
третьем, четвёртом ящике, соответственно
равны 0,6; 0,7; 0,8; 0,9. Найти вероятности
того, что деталь содержится: а) не более
чем в трёх ящиках; б) не менее чем в двух
ящиках.

Решение.

— детали нет ни в одном из
ящиков,

— деталь содержится в одном ящике,

— в двух,

— в трёх,

— в четырёх. Эти события несовместны и
образуют полную группу, поэтому
.

а)

.

Искомая
вероятность равна вероятности того,
что деталь содержится не во всех четырёх
ящиках.
.

б)
.

.

#58

Брошены три игральные кости. Найти
вероятность следующих событий: а) На
каждой из выпавших граней появиться
пять очков; б) на всех выпавших гранях
появиться одинаковое число очков.

Решение:
а) Вероятность выпадения на одной
игральной кости пяти очков равна p=1/6
.

Тогда
вероятность совместного появления 3
одинаковых событий равна P(A)=p*p*p=1/216.

б)
Из первого решения видно, что вероятность
появления на каждой из 3 граней одного
определенного очка равна P(A)=p*p*p=1/216.
Так как таких вариантов 6 ( по числу
граней кости), то вероятность появления
одинаковых очков равна P(B)=6*P(A)=6*1/216=1/36.

#59

Брошены три игральные кости. Найти
вероятности следующих событий: а) на
двух выпавших гранях появится одно
очко, а на третьей грани – другое число
очков; б) на двух выпавших гранях появится
одинаковое число очков, а на третьей
грани – другое число очков; в) на всех
выпавших гранях появится разное число
очков.

РЕШЕНИЕ.

а)
Вероятность того, что на выпавших двух
гранях появится одно очко, равна
а
вероятность того, что на другой грани
появится другое количество очков, равна

Искомую
вероятность найдем по теореме умножения
вероятностей:

.

б)
Вероятность того, что на некоторых двух
гранях выпадет одинаковое число очков,
равна

, а вероятность того, что на третьей
грани выпадет другое число очков, равна

. Искомую вероятность найдем по теореме
умножения вероятностей

в)
Количество благоприятствующих исходов
равно

общее количество элементарных исходов
равно
,
искомая вероятность равна:

.

#60

Условие:

Сколько
надо бросить игральных костей, чтобы с
вероятностью, меньшей
,
можно было ожидать, что ни на одной из
выпавших граней не появится шесть очков?

Решение:

Введем
обозначения событий:

— ни на одной из выпавших граней не
появится 6 очков;

– на выпавшей грани
кости

не появится 6 очков.

Интересующее
нас событие

состоит в совмещении событий
,

,
…,
,
т.е.

Вероятность
того, что на любой выпавшей грани появится
число очков, не равное шести, равна

События

независимы в совокупности, поэтому
применима теорема умножения:

По
условию,

. Следовательно,

. Отсюда, учитывая, что
,
найдем:

. Таким образом, искомое число игральных
костей

##61-67##

#68

В урне имеется 5 шаров с номерами от 1 до
5. Наудачу по одному извлекаются 3 шара
без возвращения. Найти вероятность
следующих событий: а) последовательно
появятся шары с номерами 1, 4, 5; б)
извлеченные шары будут иметь номера 1,
4, 5 независимо от того, в какой
последовательности они появились.

Решение:

а)
введем обозначение событий: А – выпал
шар с номером 1, В – выпал шар с номером
4, С – выпал шар с номером 5. Вероятность
наступления события А – Р(А) =

. Вероятность наступления события В при
условии, что событие А уже наступило —

(В)
=
,
вероятность события С при условии А, В
—
(С)
=

. Искомая вероятность того, что
последовательно выпадут шары с номерами
1, 4, 5 по правилу умножения равна
произведению вероятностей событий А,
В, С : Р =

=

≈ 0, 016

б) вероятность того, что шары с номерами
1, 4, 5 выпадут в произвольной последовательности
равна произведению вероятностей событий
А, В, С и количества возможных
последовательностей, которые могут
составить номера шаров :

Р
=

=

#69

Студент знает 20 из 25 вопросов программы.
Найти вероятность того, что студент
знает предложенные ему экзаменатором
3 вопроса.

Решение:
введём обозначения событий: А – студент
знает ответ на первый вопрос, В – студент
знает ответ на второй вопрос, С – студент
знает ответ на третий вопрос. Вероятность
события А равна отношению количества
вопросов которые знает студент, к общему
количеству вопросов: Р(А) =

=

. Вероятность события В при условии А —

(В)
=
,
вероятность С при условии А, В —
(С)
=

. Вероятность того, что студент знает
все три вопроса по правилу умножения
вероятностей равна : Р =

=

≈ 0, 23.

#70

В мешочке содержится 10 одинаковых
кубиков с номерами от 1 до 10. Наудачу
извлекают по одному три кубика. Найти
вероятность того, что последовательно
появятся кубики с номерами 1, 2, 3 , если
кубики извлекаются: а) без возврата; б)
с возвратом (извлеченный кубик возвращается
в мешочек).

Решение:
a) введем обозначение
событий: А – выпал кубик с номером 1, В
– выпал кубик с номером 2, С – выпал
кубик с номером 3. Вероятность наступления
события А – Р(А) =
.
Вероятность наступления события В при
условии, что событие А уже наступило —

(В)
=
,
вероятность события С при условии А, В
—
(С)
=

. Искомая вероятность того, что при
вынимании без возврата выпадут кубики
с номерами 1, 2, 3 по правилу умножения
равна произведению вероятностей событий
А, В, С : Р =

=

.

б) вероятность того, что выпадут кубики
с номерами 1, 2, 3 при вынимании их с
возвращением обратно равна произведению
равных вероятностей событий А, В, С:

Р
=

=
.

#71

По данным переписи населения (1981г.)
Англии и Уэльса установлено: темноглазые
отцы и темноглазые сыновья составили
5% обследованных лиц, темноглазые отцы
и светлоглазые сыновья — 7,9%, Светлоглазые
отцы и темноглазые сыновья – 8,9%,
Светлоглазые отцы и светлоглазые сыновья
– 78,2%. Найти связь между цветом глаз
отца и сына.

Решение:

По
условию,

Найдем условную вероятность того, что
сын темноглазый если отец темноглазый:

Найдем условную вероятность того, что
сын светлоглазый, если отец темноглазый:

Найдем условную вероятность того, что
сын темноглазый, если отец светлоглазый:

Найдем условную вероятность того, что
сын светлоглазый, если отец светлоглазый:

#72

Найти
вероятность Р(А) по данным вероятностям:

Р(АВ)=0,72,
Р(А)=0,18.

Решение.

Событие
А можно представить в виде суммы следующих
двух несовместных событий:

А=АВ+
А.
По теореме сложения вероятностей
несовместных событий получим

Р(А)=
Р(АВ+ А)=Р(АВ)+Р(А)=0,72+0,18=0,9.

Ответ:0,9

#73

Найти
вероятность

по данным вероятностям:
,

,

.

Решение.

Используя
тождество

найдём

(*)

Из
равенства

выразим
:

(**)

Подставив
(**) в (*), получим

#74

Задание:
Найти вероятность

по данным вероятностям:

Решение:
Используя тождество

, найдем
:

Подставив
в последнее равенство

(см. задачу 73), получим:

.

#75

Наступление
события
необходимо влечёт наступление события

.
Доказать, что

Решение:

По
условию, наступление события АВ влечёт
наступление события,
поэтому.

(*)

Используя
тождества
,

,

и
учитывая неравенство (*), получим

##75##

#76

Доказать,
что PA(B)≥1
— P(B)/P(A).
Предполагается, что P(A)>0.

Решение.

Справедливо
неравенство: P(A)
+ P(B) — P(AB)
≤1.

Воспользуемся
тождествами: P(AB)
= P(A)*PA(B),
P(B) = 1 –
P(B).

Подставив
P(AB) = P(A)*PA(B), P(B) = 1 – P(B) в P(A) + P(B) — P(AB)
≤1,

получим P(A) +
1 – P(B) – P(A)*PA(B) ≤1, или

P(A)*PA(B)
≥ P(A) –
P(B).

Разделив
обе части неравенства на положительное
число P(A),
окончательно имеем:

PA(B)
≥ 1 — P(B)
/ P(A)

#77

По
условию, наступление события

необходимо влечет наступление события

,
следовательно (см. задачу 48),
.
Таким образом, если будет доказано
неравенство

(*), то будет справедливо и неравенство,
указанное в условии задачи.

Докажем неравенство (*). Воспользуемся
тождествами:

(**)

Из
трех событий
,,
можно составить следующую полную группу
«сложных событий», состоящих из появлений
и непоявлений рассматриваемых трех
событий:

-появились все три события,

,,

,

,

– появилось одно событие, а два других
не появились,

– не появились все три события.

Сумма вероятностей событий, образующих
полную группу, равна единице, поэтому

Отсюда

.
(***)

Подставив (**) в (*) и используя (***), после
упрощений получим

Учитывая, что каждое слагаемое в
квадратной скобке неотрицательно,
окончательно получим

.

#78

Вывести
теорему сложения вероятностей для трех
совместных событий:

P(A + B + C) = P(A) +
P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

Предполагается,
что для двух совместных событий теорема
сложения уже доказана:

P(A1 + A2) = P(A1) +
P(A2) – P(A1A2).

Решение.

Сведем
сумму трех событий к сумме двух событий:
А + В + С = (А + В) + С.

Воспользуемся
теоремой сложения вероятностей двух
событий:

Р(А + В
+ С) = Р[(А + В) + С] = Р(А + В) + Р(С) — Р[(А + В)*С]
= Р(А + В) + Р(С) — Р[(А*С) + (В*С)]

Применим
теорему сложения вероятностей двух
совместных событий дважды (для событий
А и В, а также для событий АС и ВС):

Р(А + В
+ С) = Р(А) + Р(В) – Р(АВ) + Р(С) — {Р(АС) + Р(ВС)
– Р[(АС)(ВС)]}.

Учитывая,
что Р[(АС)(ВС)] = Р(АВС), окончательно
получим P(A
+ B + C)
= P(A)
+ P(B)
+ P(C)
– P(AB)
– P(AC)
– P(BC)
+ P(ABC).

#79

Даны
три попарно независимых события A,
B, C, которые,
однако, все три вместе произойти не
могут. Предполагая, что все они имеют
одну и ту же вероятность p,
найти наибольшее возможное значение
p.

Вероятность ошибки прибора

Вероятность отказа прибора
Вероятность отказа прибора после того, как он применялся k раз, равна p(k). Известно, что при.

Вероятность неисправности прибора
Уважаемые форумчане помогите с решением данной задачи: Мастер ищет неисправности в 6.

Найти вероятность отказа прибора
Прибор состоит из пяти последовательно включенных узлов. Вероятность отказа k-ого узла – (0,5)^k.

Найти вероятность безотказной работы прибора
Прибор состоит из двух дублирующих друг друга узлов и может работать в одном из двух режимов .

Решение

Решение

Добавлено через 1 минуту
Kitskisuli, это в уме решается. Ответ 3/8.

Найти вероятность выхода прибора из строя
Помогите пожалуйста с задачей : В условиях повышенной температуры прибор выходит из строя с.

Найти вероятность безотказной работы прибора
Прибор, работающий в течение 24 часов, состоит из 2 одинаковых блоков, в каждом из которых по 3.

Вероятность выхода электрического прибора из строя
Вероятность выхода электрического прибора из строя из-за того, что испортится электрическая цепь.

Схема Бернулли. Найти вероятность отказа прибора
Устройство состоит из 4 независимо работающих элементов. Вероятность отказов каждого из элементов.

Найти полную вероятность безотказной работы прибора
Доброго времени суток! Помогите, пожалуйста, с задачкой: Прибор состоит из 2-х дублирующих друг.

Найдите вероятность безаварийной работы прибора в течение месяца
Здравствуйте, вот условие задач. Помогите пожалуйста. Сложение совместных событий Решите.

Вероятность того что при одном измерении некоторой физической величины

Вероятность попасть в мишень при одном выстреле равна 0,8. Найдите вероятность того, что будут поражены
Биатлонист стреляет по мишеням. Вероятность попасть в мишень при одном выстреле равна 0,8. Найдите.

Найти вероятность того, что при одном выстреле цель будет поражена
Здравствуйте помогите решить задачи. Пожалуйста с решением. №6. В группе из 25 стрелков имеются.

Найти вероятность того,что при одном залпе в мишень попадет только один из стрелков.
3. Два стрелка стреляют по мишени.Вероятность попадания для первого стрелка — 0.7,а для второго -.

Найдите вероятность того, что хотя бы при одном извлечении номер шара совпадает с номером опыта
В урне имеется n одинаковых шаров с номерами от 1 до n. Шары извлекаются по одному без возвращения.

Решение

Определить вероятность того, что матожидание случайной величины положительно
Добрый день, Имеется случайная величина с неизвестных распределением, которое точно не является.

Найти вероятность того, что отклонение случайной величины от математического ожидания не превысит 0, 17
Нормально распределенная случайная величина задана плотностью распределения: (функция находиться в.

Какова вероятность того, что точка окажется в одном из треугольников ?
В трапеции ВАD = СDА = 45º, меньшая сторона основания «а», высота «h». Наудачу в трапеции.

Вероятность p того что при измерении прибором некоторой физической величины

(Сообщение отредактировал ProstoVasya 3 нояб. 2009 8:41)

(Сообщение отредактировал ProstoVasya 3 нояб. 2009 8:42)Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 3 нояб. 2009 8:39 | IP

В
зависимости от того, принимает случайная
величина только определенные дискретные
значения или может принимать любые
значения в заданном интервале она
является дискретной
или непрерывной.
Вероятность появления данного значения
дискретной случайной величины (события)
мы будем обозначать буквой р.

Вероятностные
свойства случайной величины Х
считаются заданными, если известна
функция
распределения F(x),
определяемая формулой

F(x)
= P
(X
< x),

где
х
– любое вещественное число.

Эту
функцию иногда называют интегральной
функцией распределения.

Математическое
ожидание
случайной величины совпадает с ее
средним значением, определяемым формулой
(2). Однако, учитывая повторяемость
событий, перепишем ее в виде

=
=m_x
(4)

Если
вероятности получены экспериментально
через частоты наблюдения, то иногда
используют знак * — М*
и р*.

Начальным
моментом порядка s
случайной величины х называется сумма

(5)

Эти
определения даны по аналогии с
моментом в теоретической механике.

Формула
(4) определяет первый
момент — математическое ожидание.

Введем
теперь понятие о центрированной
случайной величине.
Центри-рованной случайной величиной,
соответствующей величине Х,
называется отклонение случайной величины
от ее математического ожидания.

(6)

Очевидно, что
математическое ожидание центрированной
случайной величи-ны равно нулю,
Действительно

Ее
моменты носят название
центральных моментов.

Второй
центральный момент называется дисперсией
случайной вели-чины. Ввиду особой
важности этой величины она имеет особое
обозначение D[X].
Согласно определению имеем

D[X]
= M[(X
– m_x)²]

(7)

3.2.3. Условные вероятности. Априорная и апостериорная вероятность

При
анализе удобно рассматривать так
называемое пространство вероятно-стей,
ограниченное контуром L.
Будем считать событием попадание
слу-чайной точки внутрь контура
L
, причем попадание это в любые равновели-кие
площади считаем равновероятным. Попадание
точки внутрь контура l₁
— событие А,
а внутрь контура l₂
— событие
В. Если площади контуров l₁
l
₂ равны
соответственно S_A
и S_B
, а площадь всего контура l
— то S,
то вероят-ность
Р(А)
= S_А
/ S.

Рис.1.
Геометрическая интерпретация вероятностей

Р(В)
= S_В
/ S.
Очевидно, что имеют место неравенства


 P(A)

1 , 

P(В)

1

Обозначая
общую часть площади контуров через S_АВ.
Она соответствует одновременной
реализации событий А и В, то есть их
произведению. Как упоминалось выше,
вероятность этого случая определяется
произведением вероятностей.

P(AB)
=

Эта
вероятность называется условной
и будет обозначаться здесь как Р(В|A)
или Р(А|В)
. То есть

Р(АВ)
= Р(В|A)
P(А)=
Р(А|В) P(В)

Приведенные
зависимости уже были получены выше без
использования геометрической
интерпретации.

Рассмотрим
теперь ряд несовместных событий H₁,
H₂,
…, H_m
, образу-ющих
полную группу
событий, из
чего следует, что
.
Будем назы-вать эти события гипотезами.
Положим, что некоторое событие А может
про-изойти вместе с гипотезойH_j
с вероятностью
P(A|H_j).
Теперь определим пол-ную вероятность
события А независимо от того, какая
гипотеза реализова-лась. Очевидно, что

Так
как события АH_j
несовместны,
то, применяя формулы сложения и умножения
вероятностей, получим

Полученная
формула и есть формула полной вероятности,
позволяющая вычислить ее, зная вероятности
гипотез и условные вероятности. Для
каждого из членов последней суммы можно
записать

P(A|H_j)P(H_j)
= P(H_j|A)P(A)

Отсюда
имеем следующую важную формулу

Смысл
этой формулы состоит в том, что вероятность
гипотезы H_j
после
испытания, давшего исход А,
равна вероятности гипотезы H_j
до испытания, умноженной на вероятность
события, имевшего место при испытании,
и поделенной на полную вероятность
этого события. Полученная формула носит
название формулы
Байеса.
Поясним ее на примере решения двух
задач.

1.
Пусть имеется 4 измерительных прибора:
3 исправных и 1 неисправный.

При
измерениях исправным прибором вероятность
ошибки, превышающей допустимую р_и
= 0,04. Для неисправного прибора эта
вероятность – 0,92.

Определить
вероятность получения ошибки, превышающей
допустимую, если измерение проведено
прибором взятым наудачу (априорная
вероятность). Сформулируем условия
задачи.

Событие
А
– получение недопустимой ошибки.
Гипотеза Н₁—
взятый прибор исправен, гипотеза Н₂
– прибор неисправен.

Р(Н₁)
= 0,75; Р(Н₂)
= 0,25. Условные вероятности события А:

Р(А|H₁)
= p_и
=
0,04; Р(А|H₂)
= р_н
=
0,92.

По
формуле для полной вероятности имеем:

Р(А)
=
0,04
0,75 + 0,92 0,25 = 0,26

2.При
замере получена ошибка, превышающая
допустимое значение.

Определить
вероятность того, что измерения
проводились неисправным прибором
(апостериорная вероятность).

Воспользуемся
формулой Байеса

P(H₂|A)
=

0,884

Итак,
до испытания вероятность гипотезы Н₂
равнялась
0,25, а после испытаний выросла примерно
в 3,5 раза.

При
обратном результате измерения мы бы
имели

P(H₂|A)
=

0,027

и
вероятность гипотезы Н₂
уменьшилась
бы в примерно в 9 раз.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #