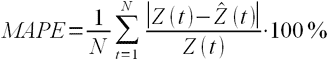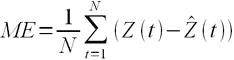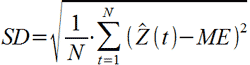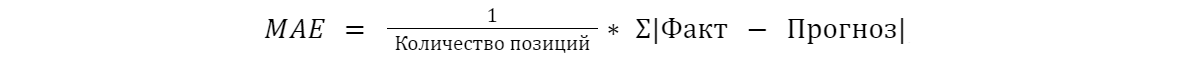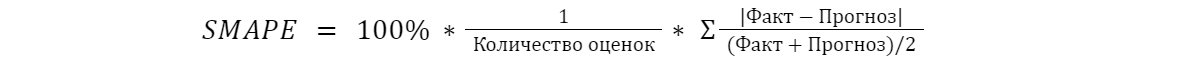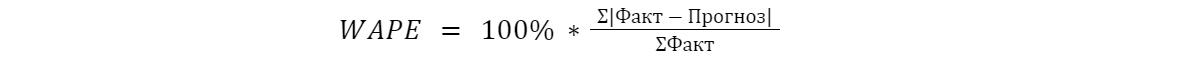Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Точность прогноза
Точность прогноза, требуемая для решения конкретной задачи, оказывает большое влияние на прогнозирующую систему. Ошибка прогноза зависит от используемой системы прогноза.
Чем больше ресурсов имеет такая система, тем больше шансов получить более точный прогноз. Однако прогнозирование не может полностью уничтожить риски при принятии решений. Поэтому всегда учитывается возможная ошибка прогнозирования.
Точность прогноза характеризуется ошибкой прогноза.
Наиболее распространенные виды ошибок:
- Средняя ошибка (СО). Она вычисляется простым усреднением ошибок на каждом шаге. Недостаток этого вида ошибки — положительные и отрицательные ошибки аннулируют друг друга.
- Средняя абсолютная ошибка (САО). Она рассчитывается как среднее абсолютных ошибок. Если она равна нулю, то мы имеем совершенный прогноз. В сравнении со средней квадратической ошибкой, эта мера «не придает слишком большого значения» выбросам.
- Сумма квадратов ошибок (SSE), среднеквадратическая ошибка. Она вычисляется как сумма (или среднее) квадратов ошибок. Это наиболее часто используемая оценка точности прогноза.
- Относительная ошибка (ОО). Предыдущие меры использовали действительные значения ошибок. Относительная ошибка выражает качество подгонки в терминах относительных ошибок.
Виды прогнозов
Прогноз может быть краткосрочным, среднесрочным и долгосрочным.
Краткосрочный прогноз представляет собой прогноз на несколько шагов вперед, т.е. осуществляется построение прогноза не более чем на 3% от объема наблюдений или на 1-3 шага вперед.
Среднесрочный прогноз — это прогноз на 3-5% от объема наблюдений, но не более 7-12 шагов вперед; также под этим типом прогноза понимают прогноз на один или половину сезонного цикла. Для построения краткосрочных и среднесрочных прогнозов вполне подходят статистические методы.
Долгосрочный прогноз — это прогноз более чем на 5% от объема наблюдений.
При построении данного типа прогнозов статистические методы практически не используются, кроме случаев очень «хороших» рядов, для которых прогноз можно просто «нарисовать».
До сих пор мы рассматривали аспекты прогнозирования, так или иначе связанные с процессом принятия решения. Существуют и другие факторы, которые необходимо учитывать при прогнозировании.
Задача 1. Известно, что анализируемый процесс относительно стабилен во времени, изменения происходят медленно, процесс не зависит от внешних факторов.
Задача 2. Анализируемый процесс нестабилен и очень сильно зависит от внешних факторов.
Решение первой задачи должно быть сосредоточено на использовании большого количества ретроспективных данных. При решении второй задачи особое внимание следует обратить на оценки специалиста в предметной области, эксперта, чтобы иметь возможность отразить в прогнозирующей модели все необходимые внешние факторы, а также уделить время для сбора данных по этим факторам (сбор внешних данных часто намного сложнее сбора внутренних данных информационной системы). Доступность данных, на основе которых будет осуществляться прогнозирование, — важный фактор построения прогнозной модели. Для возможности выполнения качественного прогноза данные должны быть представительными, точными и достоверными.
Методы прогнозирования
Методы Data Mining, при помощи которых решаются задачи прогнозирования, будут рассмотрены во втором разделе курса. Среди распространенных методов Data Mining, используемых для прогнозирования, отметим нейронные сети и линейную регрессию.
Выбор метода прогнозирования зависит от многих факторов, в том числе от параметров прогнозирования. Выбор метода следует производить с учетом всех специфических особенностей набора ретроспективных данных и целей, с которыми он строится.
Программное обеспечение Data Mining, используемое для прогнозирования, должно обеспечивать пользователя точным и достоверным прогнозом. Однако получение такого прогноза зависит не только от программного обеспечения и методов, заложенных в его основу, но также и от других факторов, среди которых полнота и достоверность исходных данных, своевременность и оперативность их пополнения, квалификация пользователя.
Ошибка
прогнозирования –
апостериорная величина отклонения
прогноза от действительного будущего
состояния объекта.
Следует
учитывать, что каждая страна имеет не
только свои модели развития, но и свои
методики и способы получения социологической
информации*.
Считается,
что любая закономерность установлена,
если вероятность ее существования
составляет более 95%.
Опыт
показывает,
что ни один из способов сам по себе не
обеспечивает высокую точность
прогноза. 100% достоверных прогнозов
не существует! Так как часто
прогнозируются очень сложные системы,
окруженные сложным фоном. Человек (как
более простая система) не может
прогнозировать на 100% более сложную
систему. Прогнозы в лучшем случае
достоверны на 80%.
Но
не учитывать любые, даже плохие прогнозы
нельзя.
Наиболее
хорошие результаты дает комплексное прогнозирование
(сочетание нескольких способов).
Статистика
по достоверности:
v
экономические прогнозы оправдываются
примерно на: 100% месячные; на 50% трехмесячные;
на 20% годовые.
v
краткосрочные прогнозы по солнечной
активности (СА) на сегодняшний день
достоверны на 70%.
v
по погоде на сегодняшний день прогнозы
достоверны на 70%.
v
по землетрясениям прогнозы достоверны
на 52%.
«Эффект
Эдипа»*, существующий в прогнозировании,
говорит, что целенаправленными решениями
и действиями (управлением) прогноз может
«самоосуществляться» или «саморазрушаться».
Точность
и достоверность прогнозов зависит от
заведомо возможных ошибок: ошибки
исходной информации, ошибки фона, ошибки
самого эксперта (исполнителя).
34. Сущность, цели и задачи оперативного планирования
Оперативное
планир-е
– завершающая часть всей системы
планирования на п/п. Его цель –
конкретизация плановых заданий на
конкретный промежуток времени, контроль
их выполнения и регулирование хода
произв-ва.
Ф-ии
оперативного планир-я:
1)оперативно-календарн.
планир-е;
2)оперативн.
управление ходом произв-ва (диспетчеризация).
В
зав-ти от того, в какой сфере и по какому
виду экон. деят-ти предприятия выделяют
операт. планир-е, его вкл-т в различные
подсистемы планир-я п/п.
Содержание
оперативного планир-я заключ-ся в
разраб-ке программ и планов на квартал,
месяц, декаду, сутки, смену для различных
структ. подразделений в зав-ти от
поставленных задач на этапе тактич.
планир-я.
Осн.
задача операт. планир-я – обеспечение
ритмичной и взаимосвяз. работы всех
подразделений и служб п/п для вып-ния
плановых заданий в установленные сроки
при исп-нии всех видов ресурсов.
В
отличие от тактич. планир-я оперативное
помимо разраб-ки планов, вкл-т и орг-цию
его непосредственного вып-ния. Операт.
планир-е должно базироваться на
технологически обоснованных прогрессивных
нормах и нормативах, а также предусматривать
применение соврем. средств научно-технич.
прогресса.
Орг-ция
опреац. планир-я способствует повышению
эф-ти работы п/п в целом за счет сокращения
и ликвидации простоев, повышению
производ-ти труда.
35. Оперативно-календарное планирование
—это
часть оперативного планир-я, которая
вкл-т разраб-ку конкретных производственных
заданий для п/п в целом и его структ.
подразделений.
Плановые
задания рассчитываются на основе норм
и нормативов, договорн. обязательств,
гос.заказа и с учетом особенностей и
условий их практической реализации.
Осн.
задачи операт. календ. планир-я:
1)планирование
и доведение до непосредственных
исполнителей оперативных плановых
заданий исходя из годовых и квартальных
объемов продукции;
2)разраб-ка
оперативно-календ. нормативов;
3)эффективное
исп-ние имеющихся ресурсов;
4)обеспечение
ритмичной работы всех подразделений;
5)планир-е
подготовки произв-ва на последующий
месяц;
6)координация
действий всех подразделений для
согласования действий по соотношению
операционных заданий;
7)корректировка
операционного плана в случае изменения
внешних и др. факторов.
Оперативно-календ
планир-е проводится в 3 этапа:
1
– объемное планирование с установлением
плановых месячных заданий для всех
структ. подразделений по всем направлениям
осн. и вспомогат. произв-ва;
2
– составление кал/пл на день/сутки;
3
– доведение плановых заданий до
непосредственных исполнителей, как
правило, имеет форму суточного или
сменного задания(наряд), которое должно
вкл-ть: объем работ/услуг в натур.
выражении, числ-ть персонала, трудозатраты,
затраты ресурсов.
В
целом операц. планир-е осущ-ся как на
общем ур-не п/п, так и на ур-не отдельных
подразделений, а оперативно-календ.
планир-е – внутри этих подразделений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами.
В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
Статистические методы
Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.
В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования.
К ним относятся:
MAPE – средняя абсолютная ошибка в процентах
где Z(t) – фактическое значение временного ряда, а 
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
ME – средняя ошибка
Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

.
SD – стандартное отклонение
где ME – есть средняя ошибка, определенная по формуле выше.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже. Скачать пример расчета в Excel >>>
Связь точности и ошибки прогнозирования
В начале этого обсуждения разберемся с определениями.
Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:
- Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
- Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.
Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.
Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)
Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:
где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
300% |
|
№3 |
1 |
4 |
75% |
Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:
В таком случае для тех же примеров ошибка рассчитается иначе:
|
вариант |
прогноз |
факт |
ошибка прогноза |
|
№1 |
4 |
0 |
100% |
|
№2 |
4 |
1 |
75% |
|
№3 |
1 |
4 |
75% |
Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.
Визуальный метод – графический
Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.
По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.


Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.
Использование формул ошибки прогнозирования на практике
Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.
Пример расчета такой оценки Вы сможете увидеть в файле Excel.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.
Для чего используется ошибка прогнозирования
В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.
Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.
В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.
Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме. Скачать пример расчета в Excel >>>
Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».
Источник: сайт http://uppravuk.net/
Сергей Смирнов, Маркетолог, Руководитель отдела развития и лицензирования Bayer.
Вместо предисловия
Соотношение между фактическими продажами и прогнозом можно описать достаточно стандартной формулой: Факт = Прогноз -/+ %(ошибка). Величина допустимой ошибки должна быть оговорена заранее, как и причины появления такой ошибки прогнозирования. На деле же получается, что величина данной ошибки может варьировать в очень широком диапазоне. Далее я постараюсь описать наиболее частые причины возникновения подобных ошибок.
Стратегия и тактика
Наиболее часто ошибки возникают тогда, когда ещё до составления прогноза были неправильно (или в полном объёме) использованы предпосылки (assumptions) для его составления. Выбор неправильной техники прогнозирования также относится к наиболее распространённым ошибкам. Вот основные виды ошибок, с которыми мне приходилось сталкиваться на практике, при прогнозировании продаж и бюджетов различных продуктов и бизнес-подразделений. Я сознательно не буду касаться ошибок, связанных с крупными изменениями в политической или экономической жизни. Обычно эти предпосылки качественно отражаются в PEST анализе бизнес- или маркетингового плана, а количественно — при непосредственном бюджетировании, в разделах “upsides & downsides”. Я же предлагаю сконцентрироваться на ошибках, возникающих на тактическом/операционном уровне.
Неправильные предпосылки: динамика рынка
Вот далеко не полный список «популярных» ошибок при прогнозировании роста (или падения) рынка:
Неправильный «перевод» динамики из рублей в евро/доллары и наоборот. Очень часто бюджет препарата строится в «валюте компании», а отчёт о продажах, на основании которого составляется прогноз – в «валюте страны», т.е.в рублях. При переводе динамики рынка из одной валюты в другую очень легко переоценить или недооценить динамику рынка. Это становится особенно важным при «фиксации» рынка в рублях, например, в сегменте госзакупок. Не добавляет ясности при прогнозировании дополнительное использование компанией «внутреннего» или «контроллингового» курса пересчёта. Причина возникновения таких ошибок кроется в прямом копировании практики прогнозов в странах со свободно-конвертируемой и стабильной валютой, с низким уровнем инфляции.Недооценка скорости выхода новых препаратов/генериков на рынок. При этом (в зависимости от жизненного цикла как рынка, так и препаратов) может наблюдаться значительное расхождение динамики рынка в SKU (или в днях лечения) и в деньгах, что увеличивает риск ошибки. Здесь причина часто кроется в недостаточном взаимодействии с регуляторным (или медицинским) отделом компании.
Злоупотребление использования CAGR на слишком новых (или быстро устаревающих) рынках. CAGR – очень полезный инструмент прогнозирования, но имеет целый ряд недостатков. Главный из них: CAGR всегда показывает «среднюю температуру по больнице»; им очень легко манипулировать, выбирая тот или иной временной промежуток. CAGR «умело» сглаживает пики и падения, оперируя лишь начальными и конечными данными продаж.
Неправильные предпосылки: доля рынка
Здесь типичная ошибка всего одна, но она состоит она из множества факторов. Эта ошибка — в определении причин (драйверов) роста препарата. Причин таких (согласно матрице Ансоффа) существует всего четыре:
Появление (рекрутинг) новых пациентов за счёт лучшей диагностики;Появление новых показаний (или off-label использование), использование в комбинированной терапииУвеличение приверженности (комплаентности) в лечении текущих пациентовПереключение с других препаратов.Очень часто эти причины не учитываются и возникают забавные парадоксы: либо сумма долей рынка препаратов становиться более 100%, либо развитие рынка перестаёт соответствовать тенденциям/стандартам в лечении того или иного заболевания. Существуют разные способы устранения таких ошибок (мнение экспертов, экстраполяция международных данных и т.п.), но самые лучшее средства здесь – логика и отличное знание своего рынка.
Неправильная техника прогнозирования: слишком простая модель
Для целого ряда сегментов (например, для инновационных онкологических и орфанных препаратов) простой «плоский» прогноз с несколькими простыми предпосылками работает плохо. Именно для таких рынков и придумали сложные пациентские модели, часто требующие значительной адаптации и доводки для наших рынков. Для этого часто стали использоваться динамические модели с обратной связью, позволяющие значительно выйти за «2-D» ограничения MS Excel (в простых электронных таблицах при этом возникает циклическая ссылка). Такое моделирование требует значительных усилий по сбору необходимых допущений и предпосылок, но это с лихвой окупается точным, понятным прогнозом и отсутствием последующих завышенных ожиданий со стороны руководства.
Неправильная техника прогнозирования: слишком сложная модель
Очевидно также и обратное: если есть упрощение модели, то также часто встречается и её ненужное усложнение. При выводе на рынок 8-го генерика строить сложную пациентскую модель явно нет необходимости. Предпосылки о занятии «z% от лидирующего продукта» или «у% от рынка к 201х году при росте а, в и с% первые три года» будет более чем достаточно.
Безусловно, в рамках такой короткой статьи невозможно коснуться целого ряда специфических ошибок, возникающих при прогнозировании. Тем не менее, хотелось бы ещё раз подчеркнуть: избежать этих ошибок помогут здравый смысл и знание своего рынка в сочетании с владением основных методов прогнозирования и статистики. Всё остальное лежит, скорее, в области искусства, чем науки.
Мы будем благодарны за Ваше мнение относительно размещенных материалов и с удовольствием разместим Ваши комментарии к соответствующим статьям/видео, а также ответим Вам лично.Ваши комментарии, статьи и видеоматериалы Вы можете присылать нам по адресу pharmaschool@comcon-2.com.

Прогнозирование показателей экономической деятельности — неотъемлемая составляющая экономического процесса. Существует множество методов прогнозирования, таких как экспертные оценки, экстраполирование, модели временных рядов, экономические системы и т. д. В этой связи возникает вопрос об оценке качества прогнозов, в том числе полученных различными способами. Также актуальным является вопрос: каким образом оценить качество прогноза до его разработки, не имея сравнительных результатов? В статье поговорим о традиционных методах оценки качества прогнозирования и важности правильного выбора.
Традиционные методы оценки качества прогнозирования
Вначале расскажем про традиционные методы оценки качества прогнозирования, которыми пользуются многие менеджеры и аналитики.
Самая популярная и общедоступная «троица» показателей представлена ниже:
- средняя абсолютная процентная ошибка (MAPE):
- средняя абсолютная ошибка (MAE):
- средняя квадратичная ошибка (RMSE):
Как правило, все останавливаются на MAPE (это средняя абсолютная процентная ошибка), потому что эта формула наиболее наглядна и понятна. В связи с простотой в понимании и удобством ее любит менеджмент, но в ней есть и нюансы, когда, например, фактические продажи меньше планируемых. Теоретически любого менеджера можно загнать в тупик, задав вопрос — какая, например, будет ошибка, если продать ноль единиц товара вместо планируемых десяти единиц?
Ошибки прогнозирования в разных условиях
Разные ошибки прогнозирования для бизнеса не являются равнозначными
Перепрогноз может приводить к:
- замораживанию средств и потере альтернативного дохода;
- излишку запасов и, как следствие, списанию и распродажам;
- низкой оборачиваемости и кассовому разрыву.
Недопрогноз ведет к:
- упущенным продажам и марже;
- низкому уровню сервиса и, соответственно, штрафам и вероятности потерять клиентов;
- непониманию реального спроса.
Разный знак ошибки — совершенно разное влияние на бизнес. Как эти знаки отражаются в ошибках? Если смотреть на среднюю абсолютную процентную ошибку (MAPE), то в перепрогнозировании ошибка скачет от 0% до бесконечности, а при недопрогнозе — от 0% до 100%. То есть мы получаем некое ассиметричное представление о том, что происходит с нашим бизнесом. При этом влияние на среднюю ошибку является равнозначным, то есть мы никак не учитываем ухудшение самого факта перепрогноза или недопрогноза.
Коварный ноль
Ноль может быть как в прогнозе, так и в продаже. Что с ним делать?
В средней абсолютной процентной ошибке (MAPE) деление на ноль не удается. Мы вынуждены выбрасывать эту ошибку или ставить 100% ошибку, что обычно и делается.
Что касается прогноза в ноль — ошибка также всегда равна там единице. Можно ли составить полное представление о бизнесе по этой ошибке? Скорее всего, нет.
То же самое со средней ошибкой — она не отражает знак ошибки, никак не реагирует на нулевые крайние случаи.
Традиционные методы оценки не всегда эффективны
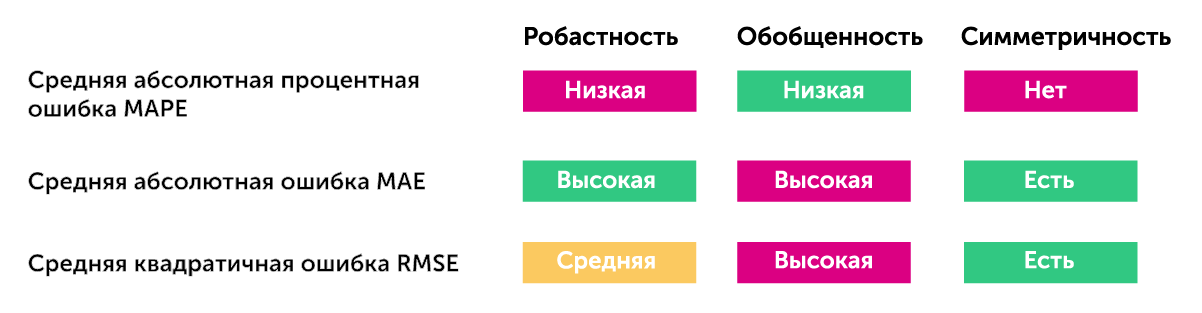
Рассмотрим причины, по которым традиционные методы оценки качества прогнозирования не всегда являются эффективными. Вышеуказанные методы обладают следующими качествами:
- робастностью — насколько ошибка устойчива при небольшом изменении — насколько она подскакивает/падает и насколько, в целом, отражает состояние бизнеса;
- обобщенностью — насколько сильно происходит усреднение ошибки — сможем ли мы составить по средней абсолютной ошибке представление о том, что происходит попозиционно (скорее всего, нет);
- симметричностью — насколько наша ошибка для разных знаков является значимой.
Как мы видим, все три вида ошибок имеют свои плюсы и минусы, но каждый раз вы склонны идти на некий компромисс, выбирая какое-то оптимальное решение.
Альтернативные методы оценки
На самом деле, этими тремя способами оценки не ограничиваются — есть и другие варианты. Мы выбрали два наиболее популярных:
- симметричная оценка качества (SMAPE):
Она, в какой-то мере, нивелирует асимметрию, которая есть в MAPE. Но есть и существенный минус — она содержит знаменательный прогноз, поэтому, угадывая нулевые продажи при прогнозировании, можно манипулировать качеством прогноза. И, в целом, SMAPE ведет к некоторому завышению прогноза, который можно смоделировать и понять;
- взвешенная абсолютная процентная ошибка прогнозирования (WAPE):
Это другая альтернатива, которая, как нам кажется, является оптимальной для оценок и неким идеальным компромиссом между сложностью интерпретации и результатом. Ее плюс заключается в том, что вы получаете больше вес по позициям — чем больше позиция продается, тем ее значимость является выше.
Стоит отметить, что не всегда бо’льшие продажи — это лучше для бизнеса, так как существует ряд позиций, которые обладают низкой маржинальностью, и, возможно, стоит взвешивать не только по количеству продаж, но и по другим показателям.
Кроме рассмотренных, есть довольно большое количество более сложных формул. Мы все время экспериментируем, находим новые варианты, но их объединяет следующее — они очень сложны для интерпретации, то есть невозможно, посчитав формулу, вывести одно сводное число, которое даст определенность и возможность принять решение. И в этом состоит основной вызов в#nbsp;прогнозировании и оценке его качества.
Почему для нас эта тема актуальна?
Команда Reshape Analytics обладает широким спектром компетенций:
- Мы проводим стратегический data-driven аудит эффективности текущей системы управления цепочкой поставок и выработка рекомендаций по ее улучшению.
- Производим анализ качества управления запасами и прогнозирование целевой эффективности внедрения аналитических решений.
- Помогаем разработать и согласовать техническое задание на внедрение систем прогнозирования и планирования.
- Разрабатываем технологические решения для упрощения интеграции с системами прогнозирования и планирования.
- Внедряем системы прогнозирования и планирования цепей поставок.
Мы можем помочь Вам разобраться во всех этих хитросплетениях и добиться максимально качественных данных для прогнозирования с помощью аналитических платформ и решений: Loginom, NOVO BI, Optimacros, Alteryx, AnyLogistix и другие.
Оставьте заявку на бесплатную консультацию, и наши специалисты помогут Вам подобрать оптимальное решение для ваших задач.
Ошибки прогнозирования
Ошибки при прогнозировании выявляются сравнением прогнозных и фактических данных. В качестве измерителя точности прогноза используются следующие характеристики:
1) среднее отклонение (или средняя ошибка), определяемое по формуле
где Yi – фактическая величина;
Fi – прогнозируемая величина; n – объем выборки.
2) среднеквадратическое отклонение ошибок (s), рассчитывается по формуле:
Среднеквадратичное отклонение используется для установления доверительных интервалов (или нижнего и верхнего контрольного уровня) изменения случайной величины. При условии, что ошибки образуют нормальное распределение, можно вычислить с определенной вероятностью доверительные пределы изменения прогнозируемой величины. Так, 95%-ный доверительный интервал рассчитывается как F±1,96s. Тогда фактическое значение (Y) будет находиться в следующих границах:
F −1,96s ≤Y ≤ F +1,96s. (5.11)
Рассмотрим пример определения доверительных интервалов изменения прогнозируемой
случайной величины.
Таблица 5.6. Данные расчета ошибки прогнозирования
Согласно прогнозу в один из дней (например, 7-й день из табл. 5.3) посетят больницу 30 пациентов. Исходя из характеристик выборки, 95%-ный доверительный интервал будет следующим: Y = 30 ± 1,96 × 4,03 = 30 ± 7,9 = 22,1 ÷ 37,9.
Итак, можно быть на 95% уверенным в том, что в этот день число пациентов может составить от 22 до 38 чел.
Возможно, вам будет интересно также:
Ошибка прогнозирования
Поскольку
будущее никогда нельзя в точности
предугадать по прошлому, то прогноз
будущего спроса всегда будет содержать
в себе ошибки в той или иной степени.
Модель экспоненциального сглаживания
прогнозирует средний уровень спроса.
Поэтому следует построить модель так,
чтобы уменьшить разность между прогнозом
и фактическим уровнем спроса. Эта
разность называется ошибкой прогнозирования.
Ошибка
прогнозирования выражается такими
показателями, как среднеквадратическое
отклонение, вариация или среднее
абсолютное отклонение. Раньше среднее
абсолютное отклонение использовалось
в качестве основного измерителя ошибки
прогнозирования при использовании
модели экспоненциального сглаживания.
Среднеквадратическое отклонение
отвергли из-за того, что рассчитывать
его сложнее, чем среднее абсолютное
отклонение, и у компьютеров на это просто
не хватало памяти. Сейчас у компьютеров
достаточно памяти, и теперь
среднеквадратическое отклонение
используется чаще.
Ошибку
прогнозирования можно определить с
помощью следующей формулы:
ОШИБКА
ПРОГНОЗА = ФАКТИЧЕСКИЙ СПРОС – ПРОГНОЗ
СПРОСА
Е
Рис. 3а. Нормальное
распределение ошибок прогноза

прогноз спроса представляет собой
среднее арифметическое фактического
спроса, то сумма ошибок прогнозирования
за определенное количество временных
периодов будет равна нулю. Следовательно,
значение ошибки можно отыскать путем
суммирования квадратов ошибок
прогнозирования, что позволяет избежать
взаимного устранения положительных и
отрицательных ошибок прогнозирования.
Эта сумма делится на количество наблюдений
и затем из нее извлекается квадратный
корень. Показатель корректируется с
уменьшением одной степени свободы,
которая теряется при составлении
прогноза. В результате, уравнение
среднеквадратического отклонения имеет
вид:

г
SE
– средняя ошибка прогнозирования; Ai
– фактический спрос в период i;
Fi
– прогноз на период i;
N
– размер временного ряда.
Ф
Рис. 3б. Скошенное
распределение ошибок прогноза
орма распределения ошибок
прогнозирования является важной, когда
формулируются вероятностные утверждения
о степени надежности прогноза. Две
типовые формы распределения ошибок
прогнозирования показаны на рисунке
3.
Полагая,
что модель прогнозирования отражает
средние значения фактического спроса
достаточно хорошо и отклонения фактических
продаж от прогноза относительно невелики
по сравнению с абсолютной величиной
продаж, то вполне вероятно предположить
нормальное распределение ошибок
прогнозирования. В тех же случаях, когда
ошибка прогнозирования сопоставима по
величине с величиной спроса, имеет место
скошенное, или усеченное нормальное
распределение ошибок прогноза.
Определить
тип распределения в конкретной ситуации
можно с помощью теста на соответствие
критерию согласия хи-квадрат. В качестве
альтернативы можно использовать другой
тест, с помощью которого можно определить,
является ли распределение симметричным
(нормальным) или экспоненциальным
(разновидность скошенного распределения):
При
нормальном распределении около 2%
наблюдаемых значений превышают значение,
равное сумме среднего и удвоенного
значения среднеквадратического
отклонения. При экспоненциальном
распределении около 2% наблюдаемых
значений превышают среднее на величину
среднеквадратического отклонения,
умноженного на коэффициент 2,75.
Следовательно, в первом случае используется
нормальное распределение, а во втором
случае – экспоненциальное.
Пример.
Снова вернемся к нашему примеру. В
базовой модели экспоненциального
сглаживания были получены следующие
результаты:
-
Квартал
I
II
III
IV
Прошлый
год1
200700
900
1
100Текущий
год1
4001
000F3
= ?Прогноз
1
200779
1
005
Оценим
стандартную ошибку прогнозирования по
данным за первый и второй кварталы
текущего года, по которым нам известны
фактические и прогнозные значения.
Допустим, что спрос имеет нормальное
распределение относительно прогноза.
Рассчитаем границы доверительного
интервала с вероятностью 95% для третьего
квартала.
Стандартная
ошибка прогнозирования:
Используя
таблицу А (см. Приложение I), определяем
коэффициент z95%
= 1,96 и получаем границы доверительного
интервала по формуле:
Y
= F3
z(SE)
=1005
1,96298
= 1064
584,2
Следовательно,
с 95%-й вероятностью границы доверительного
интервала прогноза спроса на третий
квартал текущего года составляют
значения:
420,8
< Y
< 1589,2
Точность прогноза
Точность прогноза, требуемая для решения конкретной задачи, оказывает большое влияние на прогнозирующую систему. Ошибка прогноза зависит от используемой системы прогноза.
Чем больше ресурсов имеет такая система, тем больше шансов получить более точный прогноз. Однако прогнозирование не может полностью уничтожить риски при принятии решений. Поэтому всегда учитывается возможная ошибка прогнозирования.
Точность прогноза характеризуется ошибкой прогноза.
Наиболее распространенные виды ошибок:
- Средняя ошибка (СО). Она вычисляется простым усреднением ошибок на каждом шаге. Недостаток этого вида ошибки — положительные и отрицательные ошибки аннулируют друг друга.
- Средняя абсолютная ошибка (САО). Она рассчитывается как среднее абсолютных ошибок. Если она равна нулю, то мы имеем совершенный прогноз. В сравнении со средней квадратической ошибкой, эта мера «не придает слишком большого значения» выбросам.
- Сумма квадратов ошибок (SSE), среднеквадратическая ошибка. Она вычисляется как сумма (или среднее) квадратов ошибок. Это наиболее часто используемая оценка точности прогноза.
- Относительная ошибка (ОО). Предыдущие меры использовали действительные значения ошибок. Относительная ошибка выражает качество подгонки в терминах относительных ошибок.
Виды прогнозов
Прогноз может быть краткосрочным, среднесрочным и долгосрочным.
Краткосрочный прогноз представляет собой прогноз на несколько шагов вперед, т.е. осуществляется построение прогноза не более чем на 3% от объема наблюдений или на 1-3 шага вперед.
Среднесрочный прогноз — это прогноз на 3-5% от объема наблюдений, но не более 7-12 шагов вперед; также под этим типом прогноза понимают прогноз на один или половину сезонного цикла. Для построения краткосрочных и среднесрочных прогнозов вполне подходят статистические методы.
Долгосрочный прогноз — это прогноз более чем на 5% от объема наблюдений.
При построении данного типа прогнозов статистические методы практически не используются, кроме случаев очень «хороших» рядов, для которых прогноз можно просто «нарисовать».
До сих пор мы рассматривали аспекты прогнозирования, так или иначе связанные с процессом принятия решения. Существуют и другие факторы, которые необходимо учитывать при прогнозировании.
Задача 1. Известно, что анализируемый процесс относительно стабилен во времени, изменения происходят медленно, процесс не зависит от внешних факторов.
Задача 2. Анализируемый процесс нестабилен и очень сильно зависит от внешних факторов.
Решение первой задачи должно быть сосредоточено на использовании большого количества ретроспективных данных. При решении второй задачи особое внимание следует обратить на оценки специалиста в предметной области, эксперта, чтобы иметь возможность отразить в прогнозирующей модели все необходимые внешние факторы, а также уделить время для сбора данных по этим факторам (сбор внешних данных часто намного сложнее сбора внутренних данных информационной системы). Доступность данных, на основе которых будет осуществляться прогнозирование, — важный фактор построения прогнозной модели. Для возможности выполнения качественного прогноза данные должны быть представительными, точными и достоверными.
Методы прогнозирования
Методы Data Mining, при помощи которых решаются задачи прогнозирования, будут рассмотрены во втором разделе курса. Среди распространенных методов Data Mining, используемых для прогнозирования, отметим нейронные сети и линейную регрессию.
Выбор метода прогнозирования зависит от многих факторов, в том числе от параметров прогнозирования. Выбор метода следует производить с учетом всех специфических особенностей набора ретроспективных данных и целей, с которыми он строится.
Программное обеспечение Data Mining, используемое для прогнозирования, должно обеспечивать пользователя точным и достоверным прогнозом. Однако получение такого прогноза зависит не только от программного обеспечения и методов, заложенных в его основу, но также и от других факторов, среди которых полнота и достоверность исходных данных, своевременность и оперативность их пополнения, квалификация пользователя.
From Wikipedia, the free encyclopedia
In statistics, a forecast error is the difference between the actual or real and the predicted or forecast value of a time series or any other phenomenon of interest. Since the forecast error is derived from the same scale of data, comparisons between the forecast errors of different series can only be made when the series are on the same scale.[1]
In simple cases, a forecast is compared with an outcome at a single time-point and a summary of forecast errors is constructed over a collection of such time-points. Here the forecast may be assessed using the difference or using a proportional error. By convention, the error is defined using the value of the outcome minus the value of the forecast.
In other cases, a forecast may consist of predicted values over a number of lead-times; in this case an assessment of forecast error may need to consider more general ways of assessing the match between the time-profiles of the forecast and the outcome. If a main application of the forecast is to predict when certain thresholds will be crossed, one possible way of assessing the forecast is to use the timing-error—the difference in time between when the outcome crosses the threshold and when the forecast does so. When there is interest in the maximum value being reached, assessment of forecasts can be done using any of:
- the difference of times of the peaks;
- the difference in the peak values in the forecast and outcome;
- the difference between the peak value of the outcome and the value forecast for that time point.
Forecast error can be a calendar forecast error or a cross-sectional forecast error, when we want to summarize the forecast error over a group of units. If we observe the average forecast error for a time-series of forecasts for the same product or phenomenon, then we call this a calendar forecast error or time-series forecast error. If we observe this for multiple products for the same period, then this is a cross-sectional performance error. Reference class forecasting has been developed to reduce forecast error. Combining forecasts has also been shown to reduce forecast error.[2][3]
Calculating forecast error[edit]
The forecast error is the difference between the observed value and its forecast based on all previous observations. If the error is denoted as 

where,



Forecast errors can be evaluated using a variety of methods namely mean percentage error, root mean squared error, mean absolute percentage error, mean squared error. Other methods include tracking signal and forecast bias.
For forecast errors on training data


For forecast errors on test data


Academic literature[edit]
Dreman and Berry in 1995 «Financial Analysts Journal», argued that securities analysts’ forecasts are too optimistic, and that the investment community relies too heavily on their forecasts. However, this was countered by Lawrence D. Brown in 1996 and then again in 1997 who argued that the analysts are generally more accurate than those of «naive or sophisticated time-series models» nor have the errors been increasing over time.[4][5]
Hiromichi Tamura in 2002 argued that herd-to-consensus analysts not only submit their earnings estimates that end up being close to the consensus but that their personalities strongly affect these estimates.[6]
Examples of forecasting errors[edit]
Michael Fish — A few hours before the Great Storm of 1987 broke, on 15 October 1987, he said during a forecast: «Earlier on today, apparently, a woman rang the BBC and said she heard there was a hurricane on the way. Well, if you’re watching, don’t worry, there isn’t!». The storm was the worst to hit South East England for three centuries, causing record damage and killing 19 people.[7]
Great Recession — The financial and economic «Great Recession» that erupted in 2007—arguably the worst since the Great Depression of the 1930s—was not foreseen by most forecasters, though a number of analysts had been predicting it for some time (for example, Brooksley Born, Dean Baker, Marc Faber, Fred Harrison, Raghuram Rajan, Stephen Roach, Nouriel Roubini, Peter Schiff, Gary Shilling, Robert Shiller, William White, and Meredith Whitney).[8][9][10][11] The UK’s Queen Elizabeth herself asked why had “nobody” noticed that the credit crunch was on its way, and a group of economists—experts from business, the City, its regulators, academia, and government—tried to explain in a letter.[12]
It was not just forecasting the Great Recession, but also its impact where it was clear that economists struggled. For example, in Singapore, Citi argued the country would experience «the most severe recession in Singapore’s history». The economy grew in 2009 by 3.1%, and in 2010 the nation saw a 15.2% growth rate.[13][14]
Similarly, Nouriel Roubini predicted in January 2009 that oil prices would stay below $40 for all of 2009. By the end of 2009, however, oil prices were at $80.[15][16] In March 2009, he predicted the S&P 500 would fall below 600 that year, and possibly plummet to 200.[17] It closed at over 1,115 however, up 24%, the largest single-year gain since 2003. CNBC’s Jim Cramer wrote that Roubini was «intoxicated» with his own «prescience and vision,» and should realize that things are better than he predicted; Roubini called Cramer a «buffoon,» and told him to «just shut up».[15][18] Although in April 2009, Roubini prophesied that the United States economy would decline in the final two quarters of 2009, and that the US economy would increase just 0.5% to 1% in 2010, in fact the U.S. economy in each of those six quarters increased at a 2.5% average annual rate.[19] Then in June 2009 he predicted that what he called a «perfect storm» was just around the corner, but no such perfect storm ever appeared.[20][19] In 2009 he also predicted that the US government would take over and nationalize a number of large banks; it did not happen.[21][22] In October 2009 he predicted that the price of gold «can go above $1,000, but it can’t move up 20-30%”; he was wrong, as the price of gold rose over the next 18 months, breaking through the $1,000 barrier to over $1,400.[22]
2020 Global Growth — At the end of 2019 the International Monetary Fund estimated global growth in 2020 to reach 3.4%, but as a result of the coronavirus pandemic, the IMF have revised its estimate in November 2020 to expect the global economy to shrink by 4.4%.[23][24]
See also[edit]
- Calculating demand forecast accuracy
- Errors and residuals in statistics
- Forecasting
- Forecasting accuracy
- Mean squared prediction error
- Optimism bias
- Reference class forecasting
References[edit]
- ^ 2.5 Evaluating forecast accuracy | OTexts. www.otexts.org. Retrieved 2016-05-12.
- ^ J. Scott Armstrong (2001). «Combining Forecasts». Principles of Forecasting: A Handbook for Researchers and Practitioners (PDF). Kluwer Academic Publishers.
- ^ J. Andreas Graefe; Scott Armstrong; Randall J. Jones, Jr.; Alfred G. Cuzán (2010). «Combining forecasts for predicting U.S. Presidential Election outcomes» (PDF).
- ^ Brown, Lawrence D. (1996). «Analyst Forecasting Errors and Their Implications for Security Analysis: An Alternative Perspective». Financial Analysts Journal. 52 (1): 40–47. doi:10.2469/faj.v52.n1.1965. ISSN 0015-198X. JSTOR 4479895. S2CID 153329250.
- ^ Brown, Lawrence D. (1997). «Analyst Forecasting Errors: Additional Evidence». Financial Analysts Journal. 53 (6): 81–88. doi:10.2469/faj.v53.n6.2133. ISSN 0015-198X. JSTOR 4480043. S2CID 153810721.
- ^ Tamura, Hiromichi (2002). «Individual-Analyst Characteristics and Forecast Error». Financial Analysts Journal. 58 (4): 28–35. doi:10.2469/faj.v58.n4.2452. ISSN 0015-198X. JSTOR 4480404. S2CID 154943363.
- ^ «Michael Fish revisits 1987’s Great Storm». BBC. 16 October 2017. Retrieved 16 October 2017.
- ^ Helaine Olen (March 30, 2009). «The Prime of Mr. Nouriel Roubini», Entrepreneur.
- ^ Jerry H. Tempelman (July 30, 2014). «Austrian Business Cycle Theory and the Global Financial Crisis: Confessions of a Mainstream Economist,» The Quarterly Journal of Austrian Economics]
- ^ «The Economic Crisis and the Crisis in Economics». www.eatonak.org.
- ^ Bezemer, Dirk J, 16 June 2009. «“No One Saw This Coming”: Understanding Financial Crisis Through Accounting Models»
- ^ British Academy-The Global Financial Crisis Why Didn’t Anybody Notice?-Retrieved July 27, 2015 Archived July 7, 2015, at the Wayback Machine
- ^ Chen, Xiaoping; Shao, Yuchen (2017-09-11). «Trade policies for a small open economy: The case of Singapore». The World Economy. doi:10.1111/twec.12555. ISSN 0378-5920. S2CID 158182047.
- ^ Subler, Jason (2009-01-02). «Factories slash output, jobs around world». Reuters. Retrieved 2020-09-20.
- ^ a b Joe Keohane (January 9, 2011). «That guy who called the big one? Don’t listen to him.» The Boston Globe.
- ^ Eric Tyson (2018). Personal Finance For Dummies
- ^ Maneet Ahuja (2014). The Alpha Masters; Unlocking the Genius of the World’s Top Hedge Funds
- ^ «Roubini to Cramer: ‘Just shut up’», The Los Angeles Times, April 8, 2009.
- ^ a b Daniel Altman (October 8, 2012). «Nouriel Roubini; He may not be perfect, but there’s never been a better time to be in the prophet of doom business,» Foreign Policy Magazine.
- ^ Nouriel Roubini (June 16, 2009). «Financial Gain, Economic Pain,» Project Syndicate.
- ^ Joseph Lazzaro (March 26, 2009). «‘Dr. Doom’ predicts some big banks will be nationalized,» AOL.com.
- ^ a b Alice Guy (January 16, 2023). «Seven times the experts got it very wrong on the economy,» Interactive Investor.
- ^ «IMF warns world growth slowest since financial crisis». BBC News. 2019-10-15. Retrieved 2020-11-22.
- ^ «IMF: Economy ‘losing momentum’ amid virus second wave». BBC News. 2020-11-19. Retrieved 2020-11-22.