Виды ошибок теория вероятности - Не ошибается лишь тот, кто ничего не делает!

Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.

2.1 Случайная величина

Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.

Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].

Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δ⁢x] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δ⁢x: x∈[x0,x0+δ⁢x].
Устремим интервал
δ⁢x к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w⁢(x0)=P[x0,x0+δ⁢x]δ⁢x будет оставаться конечным.
Функцию w⁢(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.

Замечание. В математической литературе распределением часто называют не функцию
w⁢(x), а её интеграл W⁢(x)=∫w⁢(x)⁢𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.

Гистограммы.

Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[k⁢h,(k+1)⁢h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.

Рис. 2.1: Пример гистограммы для нормального распределения (x¯=10,
σ=1,0, h=0,1, n=104)

Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w⁢(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w⁢(x).

Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w⁢(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.

Свойства распределений.

Из определения функции w⁢(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:

Px∈[a,b]=∫abw⁢(x)⁢𝑑x.

(2.1)

Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w⁢(x) по всей области
значений x (то есть суммарная площадь под графиком w⁢(x)) равен единице:

Это соотношение называют условием нормировки.

Среднее и дисперсия.

Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как

Переходя к пределу, получим следующее определение среднего значения
случайной величины:

где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину

σ2=(x-x¯)2¯=∫(x-x¯)2⁢w⁢𝑑x

(2.3)

называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.

Доверительный интервал.

Обозначим как P|Δ⁢x|<δ вероятность
того, что отклонение от среднего Δ⁢x=x-x¯ составит величину,
не превосходящую по модулю значение δ:

P|Δ⁢x|<δ=∫x¯-δx¯+δw⁢(x)⁢𝑑x.

(2.4)

Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.

2.2 Нормальное распределение

Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).

Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.

Плотность нормального распределения выражается следующей формулой:

w𝒩⁢(x)=12⁢π⁢σ⁢e-(x-x¯)22⁢σ2.

(2.5)

Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.

Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩⁢(x)).

При значительном отклонении x от среднего величина
w𝒩⁢(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.

Замечание. Точки x=x¯±σ являются точками
перегиба графика w⁢(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w⁢(x¯±σ)/w⁢(x¯)=e-1/2≈0,61
от высоты вершины.

Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.

x-x0σ2=2w⁢(x)σ1=1

Рис. 2.2: Плотность нормального распределения

Доверительные вероятности.

Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.

Замечание. Значение интеграла вида ∫e-x2/2⁢𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.

Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна

P|Δ⁢x|<σ=∫x¯-σx¯+σw𝒩⁢𝑑x≈0,68.

Вероятность отклонения в пределах x¯±2⁢σ:

а в пределах x¯±3⁢σ:

Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2⁢σ;x¯+2⁢σ],
и лишь 0,27% окажутся за пределами
[x¯-3⁢σ;x¯+3⁢σ].

Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.

Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись

означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δ⁢x;x¯+δ⁢x] с
вероятностью 68%. Таким образом погрешность ±δ⁢x считается
равной одному среднеквадратичному отклонению: δ⁢x=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δ⁢x=2⁢σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.

Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.

Сравнение результатов измерений.

Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.

Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2⁢σ.

Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если

Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.

Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.

Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.

2.3 Независимые величины

Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:

Обозначим отклонения величин от их средних как Δ⁢x=x-x¯ и
Δ⁢y=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δ⁢x¯=x¯-x¯=0,
Δ⁢y¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δ⁢x⋅Δ⁢y¯
равно произведению средних Δ⁢x¯⋅Δ⁢y¯
и, следовательно, равно нулю:

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=0.

(2.6)

Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.

Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2⁢x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2⁢x=2⁢σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2⁢x=2⁢σx.

Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.

Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.

Пример. Пусть σy=σx/3,
тогда σz=σx⁢1+19≈1,05⁢σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.

2.4 Погрешность среднего

Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.

Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых

Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать

σZ=σx12+σx22+…+σxn2=n⁢σx,

поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем

Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.

Подчеркнём отличия между σx и σ⟨x⟩:

величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;

величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.

2.5 Результирующая погрешность опыта

Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?

Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:

Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δ⁢xслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δ⁢xсист=x¯-xист=const:

Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:

σполн2=⟨δ⁢xсист2⟩+⟨δ⁢xслуч2⟩≤Δсист2+σслуч2.

(2.9)

Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.

Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:

Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.

Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.

Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:

Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2⁢σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)

d=386±6⁢мкм,εd=1,5%.

Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.

Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=162,0⁢м/с,
среднеквадратичное отклонение σv=13,8⁢м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6⁢м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δ⁢v, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6⁢м/с
(ε≈4%), так и значение σv≈14⁢м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.

Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=163,3⁢м/с,
σv=12,1⁢м/c, σ⟨v⟩=5⁢м/с,
σполн≈11,2⁢м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11⁢м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.

2.6 Обработка косвенных измерений

Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.

2.6.1 Случай одной переменной

Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f⁢(x).

В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:

Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δ⁢x=x-x⋆, и пользуясь определением производной,
при условии, что функция y⁢(x) — гладкая
вблизи x≈x⋆, запишем

где f′≡d⁢yd⁢x — производная фукнции f⁢(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δ⁢y2⟩,
σx2=⟨Δ⁢x2⟩), и затем снова извлечём
корень. В результате получим

Пример. Для степенной функции
y=A⁢xn имеем σy=n⁢A⁢xn-1⁢σx, откуда

σyy=n⁢σxx,или εy=n⁢εx,

то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.

Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.

Упражнение. Найдите погрешность логарифма y=ln⁡x, если известны x
и σx.

Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.

2.6.2 Случай многих переменных

Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f⁢(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:

Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:

где символом fx′≡∂⁡f∂⁡x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f⁢(x,y,…):

σu2=fx′⁣2⁢σx2+fy′⁣2⁢σy2+…

(2.11)

Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.

Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …

Остановимся на некоторых важных частных случаях формулы
(2.11).

Пример. Для суммы (или разности) u=∑i=1nai⁢xi имеем

σu2=∑i=1nai2⁢σxi2.

(2.12)

Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что

σu2u2=α2⁢σx2x2+β2⁢σy2y2+…

или через относительные погрешности

εu2=α2⁢εx2+β2⁢εy2+…

(2.13)

Пример. Вычислим погрешность произведения и частного: u=x⁢y или u=x/y.
Тогда в обоих случаях имеем

εu2=εx2+εy2,

(2.14)

то есть при умножении или делении относительные погрешности складываются
квадратично.

Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу

u=arctgyx.

В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′⁢zx′=-yx2+y2,
uy′=uz′⁢zy′=xx2+y2, и наконец

σu2=y2⁢σx2+x2⁢σy2(x2+y2)2.

Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.

По итогам данного раздела можно дать следующие практические рекомендации.

•

Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью.
•

При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной.
•

Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.

Источник

Ошибки первого и второго рода

Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.

Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.

Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.

Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.

Замечание 1.
Правильное решение может быть принято
также в двух случаях:

гипотеза принимается,
причём и в действительности она
правильная;
гипотеза отвергается,
причём и в действительности она неверна.

Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).

Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия

Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.

Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.

Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:.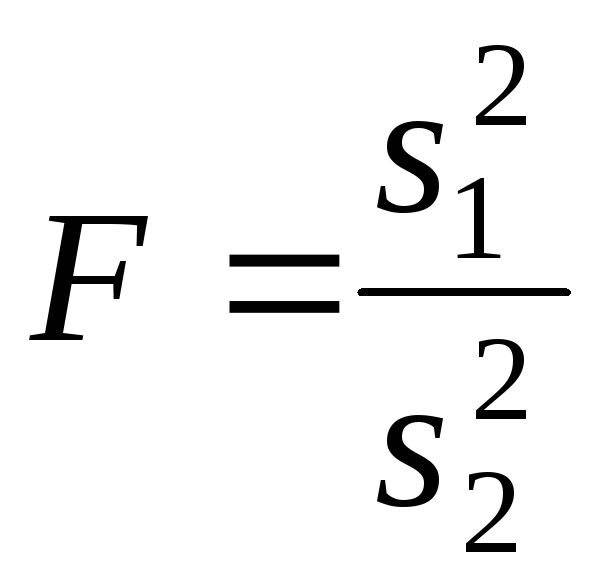

Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.

Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.

Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии,
то наблюдаемое значение критерия.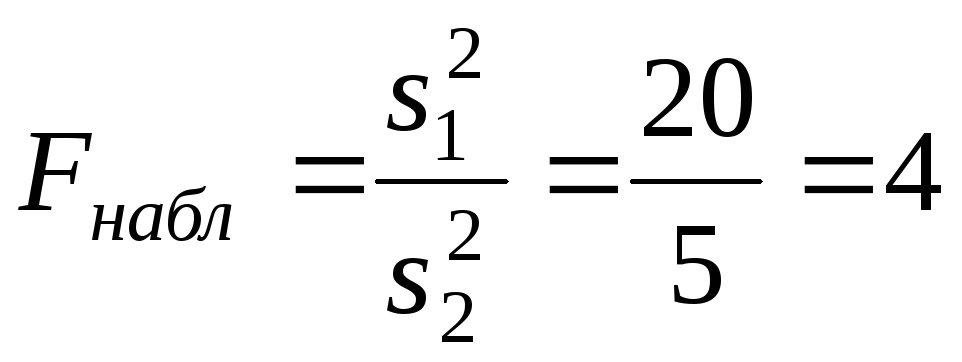

Критическая
область. Область принятия гипотезы.
Критические точки

После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.

Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.

Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.

Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.

Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.

Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.

Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.

Правосторонней
называют критическую область, определяемую
неравенством
>,
где— положительное число.

Левосторонней
называют критическую область, определяемую
неравенством
<,
где— отрицательное число.

Односторонней
называют правостороннюю или левостороннюю
критическую область.

Двусторонней
называют критическую область, определяемую
неравенствами
где.

В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):

,
или равносильным неравенством
.

Отыскание
правосторонней критической области

Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?

Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее,
была равна принятому уровню значимости:
Р(>)=.

Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.

Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>,
то нулевую гипотезу отвергают; если же<,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.

Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение

Р(>)=?
(*)

Поскольку вероятность
события
>мала (— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.

Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.

Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».

На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.

Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.

Отыскание
левосторонней и двусторонней критических
областей***

Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<(<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<)=.

Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее,
была равна принятому уровню значимости:

.
(*)

Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и(>0),
то

Учитывая (*), получим
.

Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.

Дополнительные
сведения о выборе критической области.
Мощность критерия

Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.

Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.

Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.

Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.

Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.

Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.

Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
иневозможно; если уменьшить,
тобудет возрастать. Например, если принять=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.

Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.

Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.

Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.

Соседние файлы в папке Лекции 2 семестр

Источник

2.1 Случайная величина

Гистограммы.

Рис. 2.1: Пример гистограммы для нормального распределения (x¯=10,
σ=1,0, h=0,1, n=104)

Свойства распределений.

Px∈[a,b]=∫abw⁢(x)⁢𝑑x.

(2.1)

Это соотношение называют условием нормировки.

Среднее и дисперсия.

Переходя к пределу, получим следующее определение среднего значения
случайной величины:

σ2=(x-x¯)2¯=∫(x-x¯)2⁢w⁢𝑑x

(2.3)

Доверительный интервал.

P|Δ⁢x|<δ=∫x¯-δx¯+δw⁢(x)⁢𝑑x.

(2.4)

Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.

2.2 Нормальное распределение

Плотность нормального распределения выражается следующей формулой:

w𝒩⁢(x)=12⁢π⁢σ⁢e-(x-x¯)22⁢σ2.

(2.5)

x-x0σ2=2w⁢(x)σ1=1

Рис. 2.2: Плотность нормального распределения

Доверительные вероятности.

Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.

Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна

P|Δ⁢x|<σ=∫x¯-σx¯+σw𝒩⁢𝑑x≈0,68.

Вероятность отклонения в пределах x¯±2⁢σ:

а в пределах x¯±3⁢σ:

Сравнение результатов измерений.

2.3 Независимые величины

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=0.

(2.6)

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

2.4 Погрешность среднего

σZ=σx12+σx22+…+σxn2=n⁢σx,

поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем

Подчеркнём отличия между σx и σ⟨x⟩:

2.5 Результирующая погрешность опыта

Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:

σполн2=⟨δ⁢xсист2⟩+⟨δ⁢xслуч2⟩≤Δсист2+σслуч2.

(2.9)

d=386±6⁢мкм,εd=1,5%.

Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.

2.6 Обработка косвенных измерений

2.6.1 Случай одной переменной

В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:

Пример. Для степенной функции
y=A⁢xn имеем σy=n⁢A⁢xn-1⁢σx, откуда

σyy=n⁢σxx,или εy=n⁢εx,

то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.

Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.

Упражнение. Найдите погрешность логарифма y=ln⁡x, если известны x
и σx.

Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.

2.6.2 Случай многих переменных

σu2=fx′⁣2⁢σx2+fy′⁣2⁢σy2+…

(2.11)

Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.

Остановимся на некоторых важных частных случаях формулы
(2.11).

Пример. Для суммы (или разности) u=∑i=1nai⁢xi имеем

σu2=∑i=1nai2⁢σxi2.

(2.12)

Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что

σu2u2=α2⁢σx2x2+β2⁢σy2y2+…

или через относительные погрешности

εu2=α2⁢εx2+β2⁢εy2+…

(2.13)

Пример. Вычислим погрешность произведения и частного: u=x⁢y или u=x/y.
Тогда в обоих случаях имеем

εu2=εx2+εy2,

(2.14)

то есть при умножении или делении относительные погрешности складываются
квадратично.

Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу

u=arctgyx.

В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′⁢zx′=-yx2+y2,
uy′=uz′⁢zy′=xx2+y2, и наконец

σu2=y2⁢σx2+x2⁢σy2(x2+y2)2.

По итогам данного раздела можно дать следующие практические рекомендации.

•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью.
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной.
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.

Источник

5.3. Ошибки первого и второго рода

Ошибка первого рода состоит в том, что гипотеза будет отвергнута, хотя на самом деле она правильная. Вероятность

допустить такую ошибку называют уровнем значимости и обозначают буквой («альфа»).

Ошибка второго рода состоит в том, что гипотеза будет принята, но на самом деле она неправильная. Вероятность

совершить эту ошибку обозначают буквой («бета»). Значение называют мощностью критерия – это вероятность отвержения неправильной

гипотезы.

В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения .

И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении

вероятности —

отвергнуть правильную гипотезу растёт вероятность — принять неверную гипотезу (при прочих равных условиях).

Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей и , при этом учитывается тяжесть последствий, которые

повлекут за собой та и другая ошибки.

Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару

нестатистических примеров.

Петя зарегистрировался в почтовике. По умолчанию, – он считается добропорядочным пользователем. Так считает антиспам

фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до

адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может

совершить ошибку двух типов:

1) с вероятностью ошибочно отклонить нулевую гипотезу (счесть нормальное письмо

за спам и Петю за спаммера) или
2) с вероятностью ошибочно принять нулевую гипотезу (хотя Петя редиска).

Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра

целесообразно уменьшить уровень значимости , «пожертвовав» вероятностью (увеличив её). В результате в основной ящик будут попадать все

«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью

Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность следует увеличить (в пользу уменьшения

вероятности ). Не хотел я

приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой

дилеммой. Видимо, таки, надо рассказать:

У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение

достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному

увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.

Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные

решения (упаси вас).

Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается

на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,

достаточно, возвращаемся к теме:

5.4. Процесс проверки статистической гипотезы

5.2. Нулевая и альтернативная гипотезы

| Оглавление |

Источник

Таким образом, определено положение нулевой плоскости в пластине, относительно которой соблюдается условие статического равновесия объемов в области сжимающих и растягивающих остаточных напряжений. На рис. 4 показано пространственное распределение термических (закалочных) остаточных напряжений в пластине.

Представленная в рамках данной статьи работа проводится при финансовой поддержке Правительства Российской Федерации (Минобрнауки России) в рамках комплексного проекта «Разработка и внедрение комплекса высокоэффективных технологий проектирования, конструкторско-технологической подготовки и изготовления самолета МС-21», шифр 2010-218-02-312.

Библиографический список

1. Биргер И.А. Остаточные напряжения. М.: Машгиз, 1963. 232 с.

2. Абрамов В.В. Остаточные напряжения и деформации в металлах. М.: Машиностроение, 1963. 355 с.

3. Ботвенко С.И. Остаточные напряжения и деформации при изготовлении деталей типа пластин с подкреплениями. Иркутск: Изд-во ИрГТУ, 2012. 132 с.

4. Ботвенко С.И., Огнев И.А. Теоретическое исследование пространственного распределения термических остаточных напряжений в цилиндре // Вестник ИрГТУ. 2012. №7. С. 29-36.

5. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся 13 вузов. М.: Наука, Гл. ред. физ -мат. лит., 1986. 544 с.

6. Кудрявцев Л.Д. Курс математического анализа. В 3 т. М.: Высш. шк., 1988. Т.1. 712 с. УДК 519. 21, 372.851

ТИПОЛОГИЯ ОШИБОК И ЗАБЛУЖДЕНИЙ, СВЯЗАННЫХ С ЗАДАЧАМИ КУРСА ТЕОРИИ ВЕРОЯТНОСТЕЙ. ЧАСТЬ 1: СЛУЧАЙНЫЕ СОБЫТИЯ

1Иркутский государственный университет путей сообщения, 664074, Россия, г. Иркутск, ул. Чернышевского, 15. 2Иркутский государственный университет, 664003, Россия, г. Иркутск, ул. К. Маркса, 1.

Проведён анализ и предложена типологическая структура ошибок, совершаемых студентами при изучении разделов теории вероятностей, связанных с понятием случайного события: классического определения вероятности, основных теорем о вероятности, последовательности однородных независимых испытаний. Даны методические рекомендации по совершенствованию учебного процесса. Статья адресована преподавателям математики и специалистам, которым приходится иметь дело с вероятностными методами. Библиогр. 9 назв.

Ключевые слова: случайные события; вероятность; заблуждения; методология.

TYPOLOGY OF ERRORS AND DELUSIONS ASSOCIATED WITH PROBABILITY THEORY COURSE GOALS. PART 1: STOCHASTIC EVENTS G.D. Gefan, O.V. Kuzmin

Irkutsk State University of Railway Engineering, 15 Chernyshevsky St., Irkutsk, 664074. Irkutsk State University, 1 Karl Marx St., Irkutsk, 664003.

The article presents the analysis and typological structure of students’ errors made when studying the sections of the probability theory dealing with the concept of a stochastic event: a classical definition of probability, basic probability theorems, a sequence of homogeneous independent tests. The methodic recommendations on improving the educational process are made. The article is addressed to the teachers of mathematics and specialists dealing with the probability methods. 9 sources.

Key words: stochastic events; probability; delusions; methodology.

1Гефан Григорий Давыдович, кандидат физико-математических наук, доцент кафедры математики, тел.: 89086615484, 638354, e-mail: grigef@rambler.ru

Gefan Grigoriy, Candidate of physical and mathematical sciences, Associate Professor of the Department of Mathematics of Irkutsk State Railway University, тел.: 89086615484, 638354, e-mail: grigef@rambler.ru

2Кузьмин Олег Викторович, доктор физико-математических наук, профессор, заведующий кафедрой теории вероятностей и дискретной математики, тел.: 89025604133, e-mail: quzminov@mail.ru

Kuzmin Oleg, Doctor of physical and mathematical sciences, Professor, Head of the Department of the Theory of Probability and Discrete Mathematics of Irkutsk State University, тел: 89025604133, e-mail: quzminov@mail.ru

По мнению Карла Пирсона, в математике нет другой области, в которой столь же легко допустить ошибку, как в теории вероятностей. Скорее всего, причиной является кажущаяся «очевидность», «логичность» некоторых рассуждений, опирающихся не на математический подход, а на так называемый здравый смысл. Только очень самонадеянный человек решает, например, дифференциальные уравнения, полагаясь не на теорию и строгие правила, а на догадки. Напротив, при решении задач теории вероятностей у аудитории сразу возникает целый ряд «смелых» предположений и допущений, якобы ведущих к решению. Эту активность, пожалуй, следует стимулировать и уж во всяком случае нельзя подавлять. Иная ошибка ценнее, чем безошибочные, но рутинные действия. Однако необходим анализ заблуждений, которые являются вполне типичными. Заметим сразу, что они характерны не только для начинающих: даже выдающиеся математики Лейбниц и Даламбер ошибались при решении некоторых задач теории вероятностей (об этом речь пойдёт ниже). Оговоримся также, что нас здесь интересуют лишь ошибки методологического характера, хотя студенты, конечно, совершают массу ошибок другого рода — в вычислениях, формулах и т.д.

Итак, целью данной работы является анализ и построение типологической структуры методологических ошибок и заблуждений, связанных с изучением курса теории вероятностей. Исследование опиралось на личный опыт авторов в преподавании теории вероятностей студентам разных специальностей — физико-математических, технических, экономических и на ряд известных работ, в которых вероятность рассматривается через призму парадоксов, контрпримеров, ломки стереотипов, а также с позиций непосредственного практического смысла [2, 3, 5-9].

1. Использование классического определения вероятности и элементов комбинаторики. Классическое определение вероятности — важнейшее положение теории, на котором строится решение огромного количества задач. Основной вклад в появление этого определения внёс Я. Бернулли — автор гениальной фразы «Вероятность есть степень достоверности и отличается от неё, как часть от целого» [1].

Пусть всего имеется п равновозможных элементарных исходов некоторого опыта, т из которых ведут к наступлению события А (иначе говоря, благоприятствуют этому событию). Тогда вероятность события А равна:

Р( А) = т. п

Разумеется, приведённая формула предельно проста и легко запоминается. Проблема в другом: что подразумевать под элементарными исходами при решении конкретной задачи и как эти исходы подсчитать?

Подчеркнём, что классическое определение вероятности применимо только тогда, когда различные исходы опыта обладают симметрией и поэтому рав-новозможны. Кстати, Бернулли и позже Муавр этого

обстоятельства не отмечали; требование равновоз-можности исходов было введено в классическое определение вероятности значительно позже Лапласом [4]. Неучёт этого требования приводит к ошибкам. В 1754 году Даламбер опубликовал энциклопедическую статью «Герб и решка». В частности, Даламбер утверждал, что монета, брошенная дважды, хотя бы один раз выпадет гербом с вероятностью 2/3, поскольку есть 3 возможных исхода (герб-герб, герб-решка и решка-решка), из которых первые два являются благоприятными. Разумеется, если такую ошибку совершил Даламбер (!), то рядовой ученик или студент, решая подобную задачу первый раз, обычно тоже ошибается. На самом деле, есть ещё один исход: решка-герб. Первая реакция на этот аргумент может быть недоуменной: разве это не то же самое, что герб-решка? Однако недоумение обучаемого исчезает после следующего пояснения: представьте, что монеты брошены не одновременно, а последовательно, либо представьте, что это разные монеты — скажем 1 рубль и 2 рубля. Сразу становится понятно, что герб-решка и решка-герб — это два разных элементарных исхода. Следовательно, общее число исходов равно 4, а искомая вероятность равна 3/4, а вовсе не 2/3. Можно сформулировать и иначе: исход «один герб и одна решка без указания порядка» не является элементарным и неравновозможен по отношению к исходам «два герба» и «две решки».

Уяснив необходимость равновозможности элементарных исходов для применения классического определения вероятности, обучаемый застрахует себя от ошибок при решении подобных и чуть более сложных задач. Например, требуется ответить на вопрос: почему опыт показывает, что при подбрасывании двух игральных костей сумма очков чаще равна 9, чем 10, хотя и тот и другой результат, на первый взгляд, достигается двумя способами — соответственно 9 = 3 + 6 = 4 + 5 и 10 = 4 + 6 = 5 + 5 ? Ответ ясен: на самом деле первому событию соответствует четыре благоприятных элементарных исхода (3 + 6,6 + 3,4 + 5,5 + 4), а второму — только три (4 + 6,6 + 4,5 + 5), а общее число элементарных исходов составляет 36.

В приведённых задачах исходы пересчитываются буквально «на пальцах». В более сложных случаях для применения классического определения вероятности требуется использование элементов комбинаторики. Здесь основная трудность (и, следовательно, источник ошибок) обычно состоит в выборе вида соединений (перестановки, сочетания, размещения). Конечно, можно «внушить» обучаемому, что перестановки связаны с установлением порядка среди элементов данного множества, сочетания — с выбором некоторого подмножества элементов из всего множества (без учёта порядка), размещения — и с выбором, и с установлением порядка среди выбранных элементов, но связать текст конкретной вероятностной задачи с комбинаторикой обычно весьма непросто. Универсальных рецептов для этого не существует. Клю-

чевая проблема здесь вновь упирается в описание равновозможных элементарных исходов. При этом следует иметь в виду, что равновозможные элементарные исходы не являются имманентным свойством опытов со случайными исходами, они вводятся нами (когда это возможно) для удобства вычисления вероятностей. Во многих случаях ввести множество элементарных исходов можно по-разному, и этому будет соответствовать выбор разных видов соединений.

В этом плане показательна следующая задача. Шестизначный телефонный номер содержит 2 единицы и 4 пятёрки. Однако порядок этих цифр абонент забыл. Найти вероятность того, что первая же набранная наугад комбинация этих цифр окажется правильной.

Какими элементами комбинаторики здесь воспользоваться? Однозначного ответа не существует, это зависит от того, как ввести множество равновоз-можных элементарных исходов. Ненадолго забудем о телефонных номерах. Представим, что мы имеем шесть карточек с цифрами: 5, 5, 5, 5, 1, 1. Карточки, даже если на них написана одна и та же цифра, различаем между собой (допустим, по цвету). Меняя порядок карточек, мы будем получать различные перестановки общим числом n = 6! = 720. Это и есть общее число исходов. Число благоприятных исходов здесь определяется «безболезненными» (т.е. не нарушающими правильность комбинации) перестановками карточек с пятёрками и карточек с единицами: m = 4!2!= 48. Согласно классическому определению вероятности, получаем P(A) = 48/720 = 1/15 . (Отметим, что мы не пользуемся здесь понятием перестановок с повторением элементов).

Теперь будем рассуждать принципиально иначе. Назвать некоторый телефонный номер есть не что иное, как указать номера 2-х позиций, на которых находятся единицы (пятёрки займут оставшиеся места). Количество вариантов такого выбора есть общее число равновозможных исходов. Оно равно числу сочетаний из 6 по 2:

n = C6 =-.

6 2!4!

Благоприятный исход при этом только один ( m = 1). По классическому определению вероятности снова приходим к результату P(A) = 1/15 .

Рассмотренный пример показывает, что применение комбинаторики в задачах классического определения вероятности трудно, а возможно, и не стоит определять какими-то правилами. При решении задачи нужно начинать не с того, какой вид соединений здесь использовать (тем более, что часто удаётся обойтись вообще без комбинаторики), а с выстраивания правильной схемы равновозможных элементарных исходов. Это должно подсказать тому, кто решает задачу, надо ли в ней использовать элементы комбинаторики и какие именно.

2. Задачи, связанные с теоремами сложения и умножения вероятностей. Честь окончательной

формулировки данных теорем принадлежит соответственно Байесу и Муавру. Первое наше замечание касается нахождения вероятности суммы совместных событий. Наиболее грубая ошибка заключается в том, что желая найти вероятность наступления хотя бы одного из двух событий, просто складывают их вероятности, не учитывая, что эти события совместны. Приводим задачу, над которой размышлял Я. Бернул-ли ещё до появления основных теорем теории вероятностей [4]. Двух заключённых принуждают бросить по одной игральной кости. Тот, у кого выпадет меньшее число очков, будет казнён, другой останется жив. Если же число очков окажется одинаковым, то оба избегут казни. Из 36 равновозможных исходов имеется 6 «ничейных», которые устраивают обоих заключённых. Следовательно, для каждого заключённого

существует 15 + 6 = 21 благоприятный исход, т.е.

вероятность спастись составляет 7/12. С какой вероятностью спасётся хотя бы один заключённый? Ответ очевиден — с вероятностью 1, однако простое

7/, > 1

сложение вероятностей даёт 12 12 .

С помощью диаграммы Венна легко убедиться, что вероятность суммы событий меньше суммы их вероятностей на величину вероятности произведения этих событий:

Р(А + В) = Р( А) + Р(В) — Р( АВ) .

Поэтому правильное решение приведённой задачи будет выглядеть так:

р(А + В) = У12 + ^ — 64 =1.

На вопрос «А как будет выглядеть формула для вероятности суммы трёх событий?» студенты обычно, не задумываясь, предлагают добавить в правую часть слагаемое Р(С), а вместо Р(АВ) вычитать

Р(АВС) . Это выглядит «логичным», но, разумеется, неверно. Конечно, предостерегая от этой ошибки, можно вывести формулы для вероятности суммы трёх, четырёх и большего числа событий, но разумнее, на наш взгляд, предложить следующее. Выражение «сумма перечисленных событий» имеет смысл совершенно тот же, что и выражение «хотя бы одно из перечисленных событий». Поэтому целесообразно «действовать» через противоположное событие («ни одно из перечисленных событий»). Например, сумма четырёх совместных событий имеет вероятность Р( А + В + С + В) = 1 -(1 — Р( А))х

х(1 — Р( В))(1 — Р(С))(1 — Р( В)).

Необходимо помочь студенту провести чёткую грань между понятиями «хотя бы одно из событий» (т.е. одно или более) и «одно из событий» (ровно одно, причём любое). Непонимание этого различия приводит к многочисленным ошибкам.

Наряду с совместностью событий, зависимость событий — важнейшее свойство, без правильного понимания которого невозможно усвоить основные теоремы о вероятности.

Понятие зависимости событий обычно связывают с так называемой условной вероятностью. Условной

вероятностью Р( А|В) называется вероятность события А , вычисленная при условии, что событие В произошло. Событие А называется зависимым от события В , если Р(А|В) ф Р(А).

Вероятность произведения двух событий определяется формулой

Р(АВ) = Р(В)Р(А|В) = Р(А)Р(В|А).

Если Р(А|В) = Р(А) (А не зависит от В), то и

Р(В|А) = Р(В)Р(А)/Р(А) = Р(В) ,

то есть В тоже не зависит от А. Таким образом, независимость (как и зависимость) событий взаимна. Вероятность произведения независимых событий Р(АВ) = Р(А)Р(В) .

С некоторой натяжкой можно сказать, что математическое определение зависимости (и независимости) событий соответствует нашим обычным, житейским представлениям об этом понятии. Так, большая часть аудитории относится с полным пониманием к утверждению, что не зависят друг от друга результаты бросания двух монет, двух игральных костей, даты рождения двух случайных людей и т.д. (Впрочем, кое-кто всё же имеет ошибочные представления о некотором «лимите» наступлений события по принципу «в одну воронку снаряд дважды не попадает»). Не вызывает возражений и утверждение, что шансы вытянуть единственную короткую спичку априори одинаковы у всех участников этой игры, независимо от того, в какой последовательности они тянут спички (это не столь очевидно, но легко доказывается математически с помощью приведённых выше формул). Вместе с тем, кажется, что плохо согласуется с обычным представлением о зависимости следующее важное положение теории вероятностей: два события являются либо взаимно зависимыми, либо взаимно независимыми. Простой пример: есть «метеозависимые» люди, самочувствие которых зависит от погоды, но никто никогда не слышал о том, чтобы погода зависела от здоровья людей. Но не надо упускать из виду, что в теории вероятностей речь идет не о механизме «причина-следствие», а о зависимости случайных событий. Зависит ли вероятность перемены погоды от самочувствия «метеозависимого» человека? Безусловно, зависит, поскольку плохое самочувствие с некоторой вероятностью может сигнализировать о перемене погоды. Так что это кажущееся противоречие между математикой и «здравым смыслом» довольно легко снимается.

Заметим, что определение независимости двух событий может быть дано как через понятие условной вероятности (это сделано выше), так и через равенство Р(АВ) = Р(А)Р(В). Для трёх и более событий приходится говорить, во-первых, о попарной независимости событий и, во-вторых, об их независимости в совокупности. Критерием этой совокупной независи-

мости является выполнение свойства мультипликативности

Р( АА2..А) = Р( А)Р( 4).-.Р( А)

для любого конечного набора событий из этой совокупности. Совокупно независимые события являются и попарно независимыми, а вот обратное может не выполняться — это и приводит иногда к ошибкам и недоразумениям.

Рассмотрим следующий пример. События А и В независимы, а событие С происходит в том случае, если наступает одно и только одно из событий А и В. Является ли событие С попарно независимым с событием А и с событием В ? Являются ли события А ,В и С совокупно независимыми?

Пусть Р(А) = рА, Р(В) = рВ. Тогда

Р(С) = рА (1 — рв ) + рв (1 — рА ) =

= ра + РВ — 2РаРВ .

При этом Р(С|А) = 1 — рв , Р(С|В) = 1 -рл ,

т.е. в общем случае событие с является попарно зависимым как с событием А , так и с событием В . Казалось бы, иначе и быть не может, поскольку

наступление события с связано с двумя другими событиями. Но рассмотрим частный случай: пусть А и В — появление герба при подбрасывании первой и второй монет соответственно, С — появление ровно 1 герба при подбрасывании двух монет. В этом случае Р(А) = 12, Р(В) = 12, Р(С) = 12 ,

Р(С|А) = 12, Р(С|В) = 12, т.е. событие С является попарно независимым как с событием А , так и с событием В . Однако означает ли это, что события А, В и С совокупно независимы? Положительный ответ был бы просто абсурдным, поскольку здесь информация о каких-либо двух событиях однозначно определяет информацию о третьем событии. Действительно, условие мультипликативности не выполняется, т.к. Р(АВС) = 0 (три события одновременно не могут иметь места), тогда как Р(А)Р(В)Р(С) ф 0, если только события А и В не являются ни невозможными, ни достоверными. (Например, в задаче с монетами Р(А)Р(В)Р(С) = 18). Итак, событие С может оказаться попарно независимым с событием А и с событием В , но совокупно эти три события являются зависимыми.

3. Применение формул полной вероятности и Байеса. В действительности положения, о которых идёт речь, были сформулированы не Байесом, а

Лапласом [4]. Если событие А может произойти вместе с любым из несовместных друг с другом событий

H2, …, Нп, образующих полную группу (теперь они называются гипотезами, а Лаплас называл их

«причинами»), то справедлива формула полной вероятности:

Р( А) = £ Р(И, )Р( АИг).

г=1

Если при тех же условиях известно, что в результате опыта событие А наступило, то вероятность того, что при этом имело место событие И , определяется формулой Байеса

Р( И )Р( АИ,)

Р( И,А) =

¿Р( И) Р( А|Иг)

г = 1, п

Фактически записанные формулы соответствуют двум противоположным по смыслу, хотя и близким, задачам теории вероятностей, которые можно назвать прямой и обратной. Прямая задача — найти вероятность некоторого события, учитывая все возможные, исключающие друг друга, «сценарии» его наступления (гипотезы). Обратная задача — «переоценить» вероятности «сценариев» с учётом факта наступления

события А , т.е. перейти от априорных вероятностей

Р(И ) к апостериорным условным вероятностям

Р(И|А).

Первая проблема при изучении этого материала -помочь студентам уяснить связь и различие данных задач. Образно говоря, формула полной вероятности имеет «прогностическое» назначение (каковы шансы на наступление некоторого события?), а формула Байеса — «расследовательское» (насколько вероятны различные «причины» наступившего события?).

Вторая проблема: опыт показывает, что данные формулы являются «излишне популярными» среди студентов, сплошь и рядом применяются не по назначению. Перед применением этих формул обязательно нужно проверить наличие полной группы несовместных событий И, И2,…, Ни (гипотез).

Третья проблема заключается в том, что студенты неверно определяют вероятности гипотез Р(И ) , связывая их с событием А . Никакой связи априорных вероятностей P(Hj) с событием А нет! А вот

условные вероятности Р(А|Нг) непосредственно вытекают из сформулированных в задаче условий наступления события А .

Четвёртая проблема состоит в том, чтобы уяснить, что апостериорная вероятность гипотезы может и не отличаться от априорной. Ясно, что если

Р(Нг|А) = Р(И) , то событие И не зависит от

события А. Иначе говоря, информация о наступлении события А бесполезна с точки зрения переоценки вероятности H¡. Как это может быть? Великолепной иллюстрацией такого положения является пример «математического абсурда» знаменитого писателя и

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

математика Льюиса Кэрролла, который мы приводим по книге [7]:

«Двое из трёх заключённых, обозначаемых A, B и C, будут казнены. Они это знают, но не могут догадаться, кому же из них повезёт. A рассуждает: «Вероятность, что меня казнят, равна 1/3. Если я попрошу

охранника назвать имя (отличное от моего) одного из заключённых, которых казнят, то тогда останется только две возможности. Либо другой, кого казнят, это я, либо нет, и поэтому шансы, что я выживу, увеличатся до 1/2″. Однако так же справедливо, что уже перед тем, как A спросит охранника, он знает, что одного из его компаньонов наверняка казнят, так что охранник не сообщит A никакой новой информации относительно его судьбы. Почему тогда вероятность изменилась?»

Удивительно, что Г. Секей [7], опровергая этот абсурдный результат, ограничивается достаточно общими рассуждениями, не ссылаясь на формулу Байеса. Посмотрим, как выглядит ситуация с точки зрения «байесовского подхода». Рассмотрим три гипотезы:

И — А не будет казнён (казнят В и С); Н2 — В не будет казнён (казнят А и С); Н3 — С не будет казнён (казнят А и В). Априори эти гипотезы равновероятны: Р(И) = Р(И) = Р(И) = 1/3. Событие, состоящее в том, что охранник называет, скажем, заключённого В, обозначим просто через В. Тогда по формуле полной вероятности

1Г1 + 0 +1] =1

312 J 2

Р(В) = £ Р( и )Р( Цн,)

Р(И в) =

По формуле Байеса

Р(И) Р(ВН)

Р( в)

1/6 1/2

= 1/3.

Итак, на самом деле вероятность того, что заключённый А останется в живых, не изменится после получения информации о том, что одним из казнённых окажется В (разумеется, ровно так же будет обстоять дело, если охранник назовёт имя С). Заметим, что при этом

Р( н |В)=РИШИ) =_! = 0,

21 Р( В) 1/2 ‘

Р В) = Р(н 3)Р( Вн) = 13 = 2/3. 31 Р(В) 1/2

Это означает, что печальная судьба В решена, а для С шансы спастись выросли с 1/3 до 2/3 .

Фактически, ошибка в рассуждении Льюиса Кэрролла (конечно, совершённая им намеренно), состоит в том, что после сообщения охранника шансы А и С вовсе не являются одинаковыми (исходы неравновоз-можны!). Следовательно, нельзя считать, что каждый из этих исходов имеет вероятность 1/2.

4. Повторение однородных независимых испытаний. Здесь мы не говорим о формулах Муавра-

г=1

Лапласа, поскольку они более тесно связаны с другими темами — нормальным распределением и центральной предельной теоремой — и рассматриваются во второй части статьи. Для расчёта вероятности того, что некоторое событие наступит ровно к раз в серии п однородных независимых испытаний, в каждом из которых это событие наступает с вероятностью р, служит формула Бернулли

Рп (к)=Скрк (1 — р)

к = 0, п.

При определённых условиях (вероятность р мала, число испытаний п велико) применяется формула Пуассона

Р (к) = , д = рп, к = 0, п,

^ к, > у > > ■

которую можно вывести из формулы Бернулли путём предельного перехода при р ^ 0, п ^ , .

Желательно, применив обе формулы в некотором «сомнительном» случае (например, при п = 50, р = 0.02), показать студентам неудобство формулы Бернулли и неплохую, но не слишком высокую точность пуассоновского приближения. Если этого не сделать, то есть риск, что студенты будут применять формулу Пуассона в совершенно неподходящих условиях, например, при п = 5 , р = 0.5.

Сами по себе ошибки при применении формул Бернулли и Пуассона не слишком часты и носят технический характер. Однако зачастую студент не может справиться с заданием, если оно содержит требование расчёта вероятности того, что событие наступит не просто «ровно к раз», но «хотя бы к раз», «не более к раз» и т.д. Поэтому нужна тщательная проработка этих формулировок, а соответствующие решения будут связаны с такими понятиями, как вероятность противоположного события и/или вероятность суммы событий.

Практически интересны, пожалуй, не сами значения вероятностей, даваемые формулой Бернулли, а несколько более сложные вопросы, подобные следующему. Пусть известна вероятность р наступления события в одном испытании. Сколько испытаний нужно провести, чтобы вероятность хотя бы одного наступления события в этой серии превышала 12 ?

Диалог со студентами при обсуждении этой проблемы обычно весьма интересен. Для определённости говорим о подбрасываниях игральной кости, а событие, о котором идёт речь, это появление шестёрки ( р = 16). Обычно ответ на заданный выше вопрос следующий: серия должна включать в себя более трёх подбрасываний (это «обосновывается» тем, что

3 • (16) = 12). Действительно, вероятность появления хотя бы одной шестёрки при п подбрасываниях

кости равна 1 — ^, и при п > 3 эта вероятность становится больше, чем 12. Следующий пример:

каждое испытание представляет собой подбрасывание двух костей, событие — появление двух шестёрок (р = 136). В этом случае, говорят студенты, серия должна включать в себя более 18 подбрасываний (18 • (136) = 12). Однако проверка показывает, что

вероятность 1 превышает 12 только при

п > 25, т.е. ошибка очень значительна. Здесь стоит пояснить, что если бы студенческая «логика» была правильной, то при проведении 36 подбрасываний вероятность появления хотя бы одной пары шестёрок достигала 1, а при большем числе подбрасываний -превышала бы единицу (что невозможно). Однако вряд ли нужно слишком строго относиться к этой ошибке, если учесть, что в своё время её совершил выдающийся математик и механик Кардано [7]!

Далее можно сообщить студентам о том, что в действительности существует так называемое «правило пропорциональности критических значений», которое утверждает, что если вероятность события в отдельном испытании уменьшилась в определённое число раз, то длина серии должна увеличиться в то же число раз (для того, чтобы вероятность хотя бы одного наступления события в этой серии превышала 12). Правда, как показал Муавр, это правило является верным лишь асимптотически, ошибка его применения растёт с ростом р [7]. Можно предложить

студентам проверить, как работает это правило в рассматриваемой задаче. Согласно этому правилу, учитывая, что в первом из наших примеров (подбрасывание одной кости, выпадение шестёрки) критическое значение равно 4, во втором примере (подбрасывание двух костей, выпадение двух шестёрок) критическое

значение должно увеличиться в ^ : ^^ = 6 раз и

составить 24. В действительности, как было сказано, критическое значение равно 25, и некоторое несогласование объясняется тем, что правило пропорциональности выполняется лишь асимптотически. Однако это несравнимо более точный подход, чем приведённые выше рассуждения Кардано.

Подчеркнём, что описанная учебная дискуссия является, на наш взгляд, значительно более эффективной формой обучения, чем занятие по принципу: «записал формулу — подставил значения — получил результат».

Выводы. Полностью предотвратить ошибки и заблуждения обучаемых, связанные с задачами теории вероятностей, невозможно, поскольку они, как правило, являются следствием определённых стереотипов мышления. Однако можно существенно помочь студентам, если при изучении раздела «Случайные события» уделить больше внимания:

1) требованию равновозможности элементарных исходов в классическом определении вероятности;

2) выстраиванию правильной схемы равновоз-можных элементарных исходов, что должно подсказать тому, кто решает задачу, надо ли в ней использовать элементы комбинаторики и какие именно;

3) проработке понятий совместности и независимости событий для обоснованного применения теорем сложения и умножения вероятностей;

4) уяснению связи и различия задач, требующих применения формул полной вероятности и Байеса с обязательной проверкой наличия полной группы несовместных событий (гипотез);

5) одновременному использованию формул Бер-нулли и Пуассона, иллюстрирующему условия и области их применения;

6) организации учебных дискуссий — значительно более эффективной формы обучения, чем традиционные занятия с доминирующей ролью преподавателя, где работа студентов сводится к расчётам по предлагаемым формулам.

Библиографический список

1. Бернулли Я. О законе больших чисел / пер. с лат. М.: Наука, 1986. 176 с.

2. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения. М.: Наука, 1988. 480 с.

3. Гильдерман Ю.И. Закон и случай. Новосибирск: Наука, 1991. 200 с.

4. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1988. 448 с.

5. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. М.: Наука, 1976. 168 с.

6. Колмогоров А.Н., Журбенко И.Г., Прохоров А.В. Введение в теорию вероятностей. М.: Наука, 1982. 160 с.

7. Секей Г. Парадоксы в теории вероятностей и математической статистике / пер. с англ. М.: Мир, 1990. 240 с.

8. Стоянов Й. Контрпримеры в теории вероятностей. М.: Факториал, 1999. 288 с.

9. Чубарев А.М., Холодный В.С. Невероятная вероятность. М.: Знание, 1976. 128 с.

Источник

2.1 Случайная величина

Гистограммы.

Свойства распределений.

Среднее и дисперсия.

Доверительный интервал.

2.2 Нормальное распределение

Доверительные вероятности.

Сравнение результатов измерений.

2.3 Независимые величины

2.4 Погрешность среднего

2.5 Результирующая погрешность опыта

2.6 Обработка косвенных измерений

2.6.1 Случай одной переменной

2.6.2 Случай многих переменных

Ошибки первого и второго рода

2.1 Случайная величина

Гистограммы.

Свойства распределений.

Среднее и дисперсия.

Доверительный интервал.

2.2 Нормальное распределение

Доверительные вероятности.

Сравнение результатов измерений.

2.3 Независимые величины

2.4 Погрешность среднего

2.5 Результирующая погрешность опыта

2.6 Обработка косвенных измерений

2.6.1 Случай одной переменной

2.6.2 Случай многих переменных

5.3. Ошибки первого и второго рода

Не пропустите эти материалы по теме: