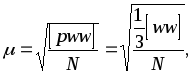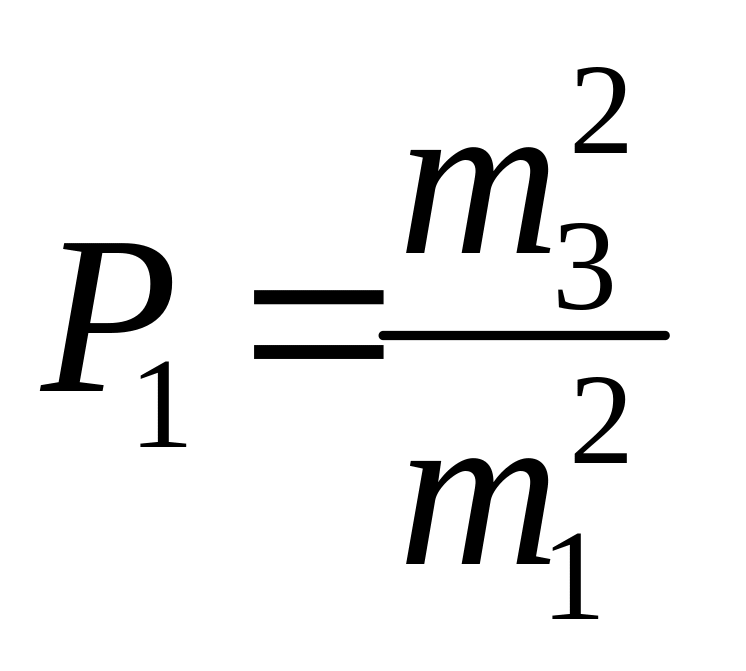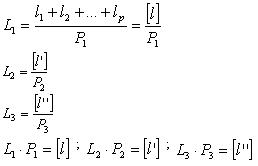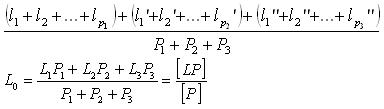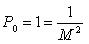Вычисление ошибки единицы веса - Не ошибается лишь тот, кто ничего не делает!

2.5.1. Вычисление
ошибки единицы веса при

установлении
весов по известным средним

квадратическим
ошибкам

Согласно (2.22) и
(2.26) имеем

откуда

(2.40)

Если при этом
известны веса, то ошибку единицы веса
можно вычислить по формуле

(2.41)

2.5.2.
Вычисление ошибки единицы веса

через
истинные ошибки

Дан ряд неравноточных
измерений

x₁, x_{2

, . . . ,}x_n

(2.42)

с соответствующими
истинными ошибками, весами и средними
квадратическими ошибками

₁
, ₂, . . . , _n
; (2.43)

p_{1

,}p₂, . . . , p_n;
(2.44)

m₁, m₂,
. . . , m_n
.
(2.45)

Умножим каждый
результат ряда (2.42) на
получим новый ряд

(2.46)

При увеличении
или уменьшении значения x
в произвольное
число раз изменяются и истинные ошибки
в соответствующее число раз

(2.47)

Соответственно

(2.48)

а это согласно
(2.41)

(2.49)

Откуда следует,
что ряд (2.46) является равноточным со
средней квадратической ошибкой 
и истинными ошибками (2.47), тогда,
использовав формулу Гаусса (1.13), получим

(2.50)

Надежность
определения 
вычислится

(2.51)

2.5.3. Вычисление средней квадратической ошибки измерения углов в триангуляции

Даны невязки в
треугольниках

w₁
, w₂
, . . . , w_n,

причем

(2.52)

Считая углы
равноточно измеренными с весом 1, находим
вес p_i
функции
_i

или

p_i
=

Так как невязки
являются истинными ошибками, воспользуемся
формулой (2.50)

где N
— число треугольников сети триангуляции.

Окончательно имеем

(2.53)

Формула (2.53) носит
название формулы
Ферреро.

2.5.4. Вычисление ошибки единицы веса через отклонения от арифметической средины

Пусть даны результаты
неравноточных измерений

x₁
, x₂
, . . . ,x_n
;

p₁
, p₂, . . . , p_n
,

а также известны
истинное значение X
и среднее арифметическое x₀.
Составим два ряда истинных ошибок
и отклонений от арифметической средины

(2.54)

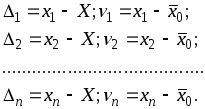
Из первого ряда
вычтем второй, в результате чего получим

(2.55)

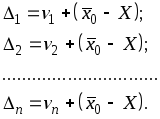
Равенства (2.55)
возведем в квадрат и умножим на
соответствующие веса. Полученные
равенства почленно просуммируем и в
результате будем иметь

(2.56)

В правой части
равенства (2.56) второе слагаемое согласно
первому свойству отклонений от общей
арифметической средины равно нулю.
Cледовательно,

(2.57)

Cогласно (2.50) имеем
,
а выражение в круглых скобках является
средней квадратической ошибкой среднего
значения, т.е.

(2.58)

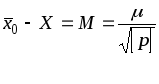
или

(2.59)

С учетом (2.58) и
(2.59) равенство (2.57) примет вид

или

Откуда

(2.60)

Надежность
определения 
вычислится

.
(2.61)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Весом измерения
(Р) называют величину, обратно
пропорциональную квадрату
среднеквадратической ошибки измерения,
принятой для всего ряда за эталон и
конкретного измерения, вес которого и
необходимо вычислить. Вес является
относительной мерой точности.

Р_i
= μ²/m_i², где Р_i
– вес i-того
измерения, m_i²
– среднеквадратическая ошибка i-того
измерения, μ – некоторая безразмерная
и произвольная величина (ошибка
конкретного измерения). Таким образом,
вес определяет соотношение точностей
эталонного и i-го
измерений. При равенстве среднеквадратических
ошибок эталонного и i-го
измерений Р_i
=1. Следовательно, μ – это среднеквадратическая
ошибка измерений, вес которой равен 1.
В практике вычислений в качестве величины
μ принимается среднеквадратическая
ошибка единицы веса .

Роль веса измерения
заключается в том, что в сложных
построениях (геодезические сети)
разнородные по своей точности измерения
приходится обрабатывать в одном
комплексе. Это порождает задачу их учета
таким образом, чтобы их влияние на
окончательный результат обработки
оказался пропорциональным их точности.
Более точные измерения должны учитываться
в построении с большим весом, а менее –
с меньшим.

Вычисление
ошибки единицы веса(μ)
производится :

Пусть
имеется ряд измерений x₁,
x₂,
x₃,
… , x_n.
Это результаты измерений одной и той
же величины. Они имеют разные ошибки
m₁,
m₂,
m₃,
… , m_n.

Таким
образом, получаем веса P₁,
P₂,
P₃,
… , P_n.
μ’ = m₃

Наиболее надежным
значением является среднее весовое:

_{где

[] – знак Гауссовой суммы}

Ошибка единицы
веса выбирается произвольно, но при
этом веса должны быть близки к 1. Это
удобно для дальнейших вычислений.

Ошибка
единицы веса:

n
– число измерений, которые используются
в обработке.

V_i
– отклонение x_i
от средне весового:

После обработки
μ’ ≈ μ.

Отклонения
V
обладают свойствами:

1.
[PV]
= 0, или должна стремиться к 0.

2.
[PV²]
= min

Вес функции

Аналогично
из P_i=
μ²
/m_i²
имеем P_F=
μ²
/m_F²
– вес функции в общем измерении.

Значение
веса функции заключается в его
использовании для оценки точности самих
функций через выражение P_F=
μ²
/m_F².
Действительно, если известны ошибки
измерений m_i
, то далее для совместной их обработки
определяются их веса с тем, чтобы
определить обратную весовую матрицу
функции.

4 Виды измерений и ошибок в геодезии и картографии. Классификация ошибок.

Виды
измерений.
Измеренная величина — это сравнение ее
с однородной ей величиной, принятой в
качестве единицы меры.

Понятие
равноточных и неравноточных измерений:
Равноточные
измерения
— однородные результаты, полученные в
одном комплексе условий: приборы,
количество приемов, технические
требования в обеспечении измерений,
однородность метеорологических условий
и.т.п.

Неравноточные
(неоднородные) – измерения, выполненные
приборами различной точности или в
существенно различных условиях.

Необходимые
и избыточные измерения:
Необходимые
измерения
— минимальное число измерений, позволяющее
получить одно единственное значение
неизвестной величины. Эти измерения не
ставят задачи уравнивания в геодезических
измерениях

Избыточные
измерения – измерения превышающие
необходимое число измерений. Играют
важную роль в геодезических измерениях
– позволяют обнаружить грубые ошибки
в измерениях и вычислениях, произвести
оценку точности всех измеренных и
вычисленных по ним величин и повысить
точность их определения.

Виды ошибок.
Ошибка- отклонение измеренной величины
от ее истинного значения

Q=x(i)
— X — истинная ошибка;
случайная ошибка V(i)=x(i)
— М[х], где x(i)-
тый результат измерения величины Х, М
– математическое ожидание; V(i)=x
— х(ср.)

Классификация
ошибок 1) по природе возникновения:

1. Инструментальные
ошибки — ошибки юстировки инструмента,
деления вертикального круга, микрометра
(рен, случайные ошибки, систематические
ошибки).

2. Ошибки за
влияние внешних условий — преломление
лучей, неравномерность освещения,
кручение сигнала, неустойчивость
инструмента, температурное влияние
и.т.д.

3. Ошибки за
влияние среды – рефракция, туман,
действие ветра, воздушн.потоки и др.

4. Личные ошибки
– ошибки конкретного наблюдателя,
зависят от остроты зрения и опыта работы
наблюдателя.

2) по характеру:

1. Грубые –
являются следствием каких-либо просчетов
наблюдателя, неисправностей приборов,
их смещений в момент измерений, неверной
методики, резкого ухудшения внешних
условий и др. Измерения с грубыми ошибками
отбраковывают.

2. Случайные –
элементарные ошибки (приборные, вызываемые
неточностью при изготовлении и сборке
деталей приборов; ошибки внешних условий,
личные), математическое ожидание которых
равно 0. Случайные ошибки по величине
обычно больше систематических, но за
счет взаимных компенсаций оказывают
меньшее влияние на окончательные
результаты.

3. Систематические
– элементарные ошибки, матем.ожидание
которых отлично от 0. Их величина зависит
от применяемой методики. Систематические
ошибки по характеру действия делят на:
а) постоянные – сохраняют знак и величину;
б) односторонне действующие, меняющиеся
по величине, но сохраняющие знак; в)
функциональные – изменяющиеся по
какому-либо закону.

Случайные ошибки
можно рассматривать как суммарную
случайную величину, для которой
справедлива теорема Ляпунова: Если
некоторая случайная величина есть сумма
достаточно большого числа независимых
случайных величин, отклоняющихся от
математического ожидания на величину
значительно меньшую суммы случайной
величины, то закономерность распределения
суммы величины близка к нормальной.

Т.Л. позволяет
унифицировать подход в уравнивании
всех случайных величин в геодезии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.

По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.

Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.

Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)

Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:

1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.

Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)

где: ;
n – количество измерений одной величины.

Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.

Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.

Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:

F = f( X, Y, Z … ), (1.28)

здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.

В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
(1.29)

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.

Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:

Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)

Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)

Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим

В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)

Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,

F = x * y * z,

то для нее можно записать выражение относительной ошибки функции:
(1.33)

которое в некоторых случаях оказывается более удобным, чем формула (1.32).

Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)

Величина (1.36)

называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде

по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде

и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

или

Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:

M2 = m2/n

или
(1.37)

то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.

Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.

Пусть имеется ряд равноточных измерений величины X:

l1, l2 , …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем разности:
(1.38)

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:

[V] = 0. (1.39)

Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)

Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:
(1.41)

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.

Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.

Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)

Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,

,
откуда ;

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).

Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)

Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.

Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:

p = C/m2 (1.45)

где C – в общем случае произвольное положительное число.

При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .

Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем

откуда (1.47)

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)

Согласно (1.46) и (1.32) напишем:

Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:

Подставим это выражение в формулу (1.48) и получим,

P = [p], (1.49)

то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.

В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:

P = n. (1.50)

При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)

где pi – вес i-того элемента.

Теория ошибок измерений

Теория ошибок измерений изучает свойства ошибок и законы их
распределения, методы обработки измерений с учетом их ошибок, а также способы
вычисления числовых характеристик точности измерений. При многократных
измерениях одной и той же величины резуль таты измерений получаются
неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются
разными по величине и по знаку ошибками. Задача теории ошибок — нахождение
наиболее надежного значения измеренной величины, оценка точности результатов
измерений и их функций и установление допусков, ограничивающих использование
результатов обработки измерений.

По своей природе ошибки бывают грубые, систематические и
случайные.

Грубые ошибки являются результатом промахов и просчетов. Их
можно избежать при внимательном и аккуратном отношении к работе и организации
надежного полевого контроля измерений. В теории ошибок грубые ошибки не
изучаются.

Систематические ошибки имеют определенный источник,
направление и величину. Если источник систематической ошибки обнаружен и изучен,
то можно получить формулу влияния этой ошибки на результат измерения и затем
ввести в него поправку; это исключит влияние систематической ошибки. Пока
источник какой-либо систематической ошибки не найден, приходится считать ее
случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа
измерений (строгостью теории), точностью измерительного прибора, квалификацией
исполнителя и влиянием внешних условий. Закономерности случайных ошибок
проявляются в массе, то есть, при большом количестве измерений; такие
закономерности называют статистическими. Освободить результат единичного
измерения от случайных ошибок невозможно; невозможно также предсказать случайную
ошибку единичного измерения. Теория ошибок занимается в основном изучением
случайных ошибок.

Случайная истинная ошибка измерения Δ — это разность между
измеренным значением величины l и ее истинным значением X:

(1.25)

Свойства случайных ошибок. Случайные ошибки подчиняются
некоторым закономерностям:

при данных условиях измерений абсолютные значения случайных
ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот
предел, она считается грубой,

положительные и отрицательные случайные ошибки равно
возможны,

среднее арифметическое случайных ошибок стремится к нулю
при неограниченном возрастании числа измерений. Третье свойство случайных ошибок
записывается так:

(1.26)

малые по абсолютной величине случайные ошибки встречаются
чаще, чем большие.

Кроме того, во всей массе случайных ошибок не должно быть
явных закономерностей ни по знаку, ни по величине. Если закономерность
обнаруживается, значит здесь сказывается влияние какой-то систематической
ошибки.

Средняя квадратическая ошибка одного измерения. Для оценки
точности измерений можно применять разные критерии; в геодезии таким критерием
является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же
разработал основные положения теории ошибок. Средняя квадратическая ошибка
одного измерения обозначается буквой m и вычисляется по формуле Гаусса:

(1.27)

где: ;
n — количество измерений одной величины.

Средняя квадратическая ошибка очень чувствительна к большим
по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то
же время она является устойчивым критерием для оценки точности даже при
небольшом количество измерений; начиная с некоторого n дальнейшее увеличение
числа измерений почти не изменяет значения m; доказано, что уже при n = 8
значение m получается достаточно надежным.

Предельная ошибка ряда измерений обозначается Δпред; она
обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m
при практических измерениях. Считается, что из тысячи измерений только три
ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической
относительной ошибкой; для некоторых видов измерений относительная ошибка более
наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1,
например, mx/X = 1/10 000.

Средняя квадратическая ошибка функции измеренных величин.
Выведем формулу средней квадратической ошибки функции нескольких аргументов
произвольного вида:

F = f( X, Y, Z … ), (1.28)

здесь: X, Y, Z … — истинные значения аргументов,
F — истинное значение функции.

В результате измерений получены измеренные значения
аргументов lX, lY, lZ, при этом:

(1.29)

где ΔX, ΔY, ΔZ — случайные истинные ошибки измерения
аргументов.

Функцию F можно выразить через измеренные значения
аргуметов и их истинные ошибки:

Разложим функцию F в ряд Тейлора, ограничившись первой
степенью малых приращений ΔX, ΔY, ΔZ:

(1.30)

Разность является
случайной истинной ошибкой функции с противоположным знаком, поэтому:

(1.31)

В силу третьего свойства случайных ошибок члены, содержащие
произведения случайных ошибок, будут незначительными по величине, и их можно не
учитывать; таким образом,

(1.32)

Как частные случаи формулы (1.32) можно написать выражения
для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,

F = x * y * z,

то для нее можно записать выражение относительной ошибки
функции:

(1.33)

которое в некоторых случаях оказывается более удобным, чем
формула (1.32).

Принцип равных влияний. В геодезии часто приходится
определять средние квадратические ошибки аргументов по заданной средней
квадратической ошибке функции. Если аргумент всего один, то решение задачи не
представляет трудности. Если число аргументов t больше одного, то возникает
задача нахождения t неизвестных из одного уравнения, которую можно решить,
применяя принцип равных влияний. Согласно этому принципу все слагаемые правой
части формулы (1.32) или (1.33) считаются равными между собой.

Арифметическая середина. Пусть имеется n измерений одной
величины X, то-есть,

(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и
получим:

(1.35)

Величина (1.36)

называется средним арифметическим или простой
арифметической серединой. Запишем (1.35) в виде

по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества
измерений простая арифметическая середина стремится к истинному значению
измеряемой величины. При ограниченном количестве измерений арифметическая
середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде

и подсчитаем среднюю квадратическую ошибку арифметической
середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

или

Но ml1 = ml2 = … = mln= m по условию задачи, так как
величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках
будет n * m2, одно n сократится и в итоге получим:

M2 = m2/n

или

(1.37)

то-есть, средняя квадратическая ошибка арифметической
середины в корень из n раз меньше ошибки одного измерения.

Вычисление средней квадратической ошибки по уклонениям от
арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических
выкладках и при исследованиях приборов и методов измерений, когда известно
истинное значение измеряемой величины. На практике оно, как правило, неизвестно,
и оценку точности выполняют по уклонениям от арифметической середины.

Пусть имеется ряд равноточных измерений величины X:

l1, l2 , …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем
разности:

(1.38)

Сложим все разности и получим [l] — n * X0 = [V]. По
определению арифметической середины n * X0 = [l], поэтому:

[V] = 0. (1.39)

Величины V называют вероятнейшими ошибками измерений;
именно по их значениям и вычисляют на практике среднюю квадратическую ошибку
одного измерения, используя для этого формулу Бесселя:

(1.40)

Приведем вывод этой формулы. Образуем разности случайных
истинных ошибок измерений Δ и вероятнейших ошибок V:

(1.41)

Разность (X0 — X) равна истинной ошибке арифметической
середины; обозначим ее Δ0 и перепишем уравнения (1.41):

(1.42)

Возведем все уравнения (1.42) в квадрат, сложим их и
получим:

Второе слагаемое в правой части этого выражения равно нулю
по свойству (1.39), следовательно,

Разделим это уравнение на n и учтя, что [Δ2]/n =m2,
получим:

(1.43)

Заменим истинную ошибку арифметической середины Δ0 ее
средней квадратической ошибкой ; такая замена
практически не изменит правой части формулы (1.43). Итак,

,
откуда ;

после перенесения (n-1) в правую часть и извлечения
квадратного корня получается формула Бесселя (1.40).

Для вычисления средней квадратической ошибки арифметической
середины на основании (1.37) получается формула:

(1.44)

Веса измерений. Измерения бывают равноточные и
неравноточные. Например, один и тот же угол можно измерить точным или
техническим теодолитом, и результаты таких измерений будут неравноточными. Или
один и тот же угол можно измерить разным количеством приемов; результаты тоже
будут неравноточными. Понятно, что средние квадратические ошибки неравноточных
измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с
большей точностью (с меньшей ошибкой), заслуживает большего доверия.

Вес измерения — это условное число, характеризующее
надежность измерения, степень его доверия; вес обозначается буквой p. Значение
веса измерения получают по формуле:

p = C/m2 (1.45)

где C — в общем случае произвольное положительное число.

При неравноточных измерениях одной величины наиболее
надежное ее значение получают по формуле средневесовой арифметической середины:

(1.46)

или X0 = [l*p] / [p] .

Ошибку измерения, вес которого равен 1, называют средней
квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы
(1.45) получаем

откуда (1.47)

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По
определению веса имеем:

(1.48)

Согласно (1.46) и (1.32) напишем:

Подставим сюда вместо mli2 их выражения через вес m2 = C/p
, тогда:

Подставим это выражение в формулу (1.48) и получим,

P = [p], (1.49)

то-есть, вес средневесовой арифметической середины равен
сумме весов отдельных измерений.

В случае равноточных измерений, когда веса всех измерений
одинаковы и равны единице, формула (1.49) принимает вид:

P = n. (1.50)

При обработке больших групп измерений (при уравнивании
геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса
измерений и других элементов после уравнивания, а ошибка любого уравненного
элемента подсчитывается по формуле:

(1.51)

где pi — вес i-того элемента.

Пусть имеем ряд равноточных измерений одной и той же величины, из которых образовано 3 группы:

Для каждой группы измерений можно получить среднее значение:

Результаты L1, L2, L3 – неравноточные, так как получены из разного числа измерений и имеют разные веса Р1, Р2, Р3.
Из первоначального ряда равноточных измерений можно найти арифметическую средину:

Эта формула представляет общую арифметическую средину или весовое среднее, получаемую из неравноточных измерений L1, L2, L3 с весами P1, P2, P3. Вес общей арифметической средины равен сумме весов.

Средние квадратические ошибки неравноточных измерений различны, поэтому для оценки точности таких измерений выбирают общую меру. Такой мерой является средняя квадратическая ошибка такого измерения, вес которого равен единице.
Следует отметить, что величина М (средняя квадратическая ошибка веса) может относится к воображаемому измерению, если среди результатов нет ни одного с весом равным единице.

Установим связь между средней квадратической ошибкой единицы веса М и средней квадратической ошибкой результата измерений с весом

Чтобы увидеть самое интересное, Вам необходимо авторизоваться/зарегистрироваться

Только зарегистрированные и авторизованные пользователи могут оставлять комментарии.

Добро пожаловать!

Войдите или зарегистрируйтесь сейчас!

Войти

Регистрация:

17 янв 2014

Сообщения:

10

Симпатии:

0

Здравствуйте дорогие форумчане. Я не совсем геодезист, занимаюсь гидрографией. Но приходится зачастую делать съёмку берегов, причалов, островов. Пользуюсь Credo, и в принципе особеных сложностей с ним не возникало. Скачиваем, импортируем, предабрабатываеи, уравниваем. Исправляем ошибки. Смотрим, что получилось. Сейчас захотелось основательно разобраться с тем, что мы там считаем, не по наитию и не халтурно, как это было раньше. Вроде всё сидит и ладно. Чаще всего выполняем съёмку 500-го масштаба. Прибор двухсекундник. Для топосъёмки развиваем съёмочную сеть.
Так вот возникает ряд вопросов, если не трудно, подскажите, пожалуйста.
1) Какой класс точности для пунктов съёмочной сети устанавливать в Credo? В соответстви с полученной точностью? Вы спросите, а какой вам нужен? А я не знаю, есть ли для съёмочной сети какие-либо требования? Ставлю обычно ОМС 2-го разряда, потому как разрешает 14 секунд между полуприёмами, куда чаще я и поподаю, точнее не получается или что то с прибором.
2) В СП 11-104-97 в п.5.25 говорится, что погрешности положения пунктов не должны превышать 0,1 мм в масштабе плана…. Это не более 5 см для М 1:500. Где это посмотреть в Кредо? В какой ведомости? m – что ли?
3) В ведомости оценки точности плановой сети что значит СКО направлений фактическое 23, Априорная 7? В чём оно в градусах? А ppm что такое?
4) А в ведомости характеристика теодолитных ходов Fb факт. -0°00’57» больше чем допустимое Fb доп. 0°00’45» значит плохо что ли? Что такое S/Fs 25891 и каким оно должно быть?
5) После уравнивание какие-то доверительные интервалы выскакивают? Какая то теория вероятностей:
Априорные характеристики:
Доверительная вероятность: α = 0.955
СКО единицы веса: μ = 1.000
Доверительные границы: 0.593 < σ < 2.957
По результатам уравнивания:
СКО единицы веса: μ = 1.315
Доверительные границы: 0.779 < σ < 3.889
Это зачем? О чём говорит и сколько надо, чем меньше тем лучше и чтоб поподал в интервалы?
6) В ГКИНП-02-033-82 (ИНСТРУКЦИЯ ПО ТОПОГРАФИЧЕСКОЙ СЪЕМКЕ В МАСШТАБАХ 1:5000, 1:2000, 1:1000 и 1:500) Таблица 14.Что такое ms = 0,2 мм, ms = 0,3 мм и 1/N: 1/2000, 1/3000
На что вообще следует смотреть при обработке данных в кредо, в смысле оценки точности измерений.
Ясно, что общей теории не хватает. Но после поисков и чтения различных инструкций и снипов, каши в голове не поубавилось. Извините, что так много вопросов в одном посту.

#1
Форумчанин

Слава Голубцов,

Именно. Но как правило 95% геодезистов не хватает
1.Тут пляшите либо от инструкции(если на неё ориентируетесь) либо от своего прибора. Можно создать свой класс с точностями прибора (направления и расстояния).
2.Да, m- это погрешность, она же СКО (среднеквадратическое отклонение)
3.Априорная- до уравнивания. Т.е. по выставленным классам программа прикидывает что должно получиться. У Вас может получиться чуть больше, т.к. программа учитывает только ошибки инструмента (без ошибок центрировки и наведения). В данном случае указано в секундах
ppm- parts per million, т.е. можно понимать как миллиметров на километр. ошибка в 2 ppm означает 2 мм на 1 км. Т.е. у линии длинной 200 м ско будет 0,4 мм
4.Да, в допуски надо попадать. Допуски устанавливаются для класса или инструкцией. формула (доверительный коэффициент)*(точность измерения углов)*(корень из количества станций). первые 2 указаны в инструкции, хотя обычно указана просто формула на количество станций. В кредо доверительный коэффициент выбирается в свойствах проекта, точность берется из класса точности. Если Вы не ориентируетесь на инструкцию, то поставьте его 3.
5.Про разбор этого уже когда-то писалось

#2
Регистрация:

17 янв 2014

Сообщения:

10

Симпатии:

0

Сева Папкин, Спасибо большое., помогли разобраться. Пока писал сообщение сам много понял, и вы разъяснили.

#3

Поделиться этой страницей

Источник

На чтение 9 мин Просмотров 1.5к. Опубликовано 03.10.2021

По своей природе ошибки бывают грубые, систематические и случайные.

Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:

где: ;
n – количество измерений одной величины.

F = f( X, Y, Z … ), (1.28)

здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.

В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
(1.29)

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.

Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)

F = x * y * z,

то для нее можно записать выражение относительной ошибки функции:
(1.33)

которое в некоторых случаях оказывается более удобным, чем формула (1.32).

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)

Величина (1.36)

M2 = m2/n

или
(1.37)

Пусть имеется ряд равноточных измерений величины X:

l1, l2 , …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем разности:
(1.38)

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:

[V] = 0. (1.39)

Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.

Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)

,
откуда ;

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).

p = C/m2 (1.45)

где C – в общем случае произвольное положительное число.

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)

P = [p], (1.49)

то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.

P = n. (1.50)

где pi – вес i-того элемента.

Источник

2.5.3. Вычисление средней квадратической ошибки измерения углов в триангуляции

2.5.4. Вычисление ошибки единицы веса через отклонения от арифметической средины

4 Виды измерений и ошибок в геодезии и картографии. Классификация ошибок.

Теория ошибок измерений

Добро пожаловать!

Форумчанин

Поделиться этой страницей