Ячейка должна содержать формулу ошибка

Ошибки при работе со средством «Подбор параметра»

После
того как вы щелкнете на кнопке ОК в
диалоговом окне Подбор
параметра, чтобы найти нужное значение,
Excel
вместо диа­логового окна Результат
подбора параметра может вывести на
экран одно из следующих сообщений об
ошибке.

Ячейка
должна содержать формулу.
Это сообщение об ошибке появляется
тогда, когда ячейка, адрес которой
указан в поле ввода Установить
в ячейке диалогового окна Подбор
параметра, не содержит формулы.
Чаще всего причиной этой ошибки является
то, что вы в этом поле ввели адрес ячейки,
который должен быть указан в поле ввода
Изменяя значение ячейки. Чтобы исправить
эту ошибку, закройте
сначала сообщение об ошибке, а затем
введите в поле Установить в ячейке
адрес «правильной» ячейки, содержащей
формулу. Затем сно­ва
щелкните на кнопке ОК.

Введено
недопустимое значение. Следует ввести
число.
Это сооб­щение
об ошибке появляется тогда, когда вы в
поле ввода Значение кроме
числа ввели еще какие-то символы, которые
Excel
не может распознать
как числа. Чтобы исправить эту ошибку,
закройте сначала сообщение
об ошибке, а затем введите в поле Значение
правильное число (целое или десятичное).
Затем снова щелкните на кнопке ОК.

В
поле ввода Значение
к числу можно добавить знак денежной
единицы или процента

Ячейка
должна содержать значение.
Это сообщение об ошибке появляется
тогда, когда ячейка, адрес которой
указан в поле ввода Изменяя
значение ячейки
диалогового окна Подбор
параметра,
не со­держит
числового значения (а содержит, например,
текст или фор­мулу).
Чтобы исправить эту ошибку, закройте
сначала сообщение об ошибке,
а затем введите в поле Изменяя
значение ячейки адрес
«пра­вильной»
ячейки, содержащей числовое значение.
Затем снова щел­кните
на кнопке ОК.

Введенный
текст не является правильной ссылкой
или именем.
Это сообщение
об ошибке появляется тогда, когда в
поле ввода Установить
в
ячейке
или в поле ввода Изменяя
значение ячейки
диалогового окна Подбор
параметра
введено нечто, что Excel
не может распознать как ссылку
на ячейку. Чаще всего такая ошибка
возникает тогда, когда вы вручную
вводите адрес ячейки, а не указываете
ячейку путем щелчка на
ней. (Например, если вы вводите адрес
ячейки «русскими» бук­вами.)
Чтобы исправить эту ошибку, закройте
сначала сообщение об ошибке,
а затем введите в поле ввода правильный
адрес ячейки. Затем снова
щелкните на кнопке ОК.

Решение
не найдено.
Это сообщение появляется в диалоговом
окне
Результат
подбора параметра
(а не как сообщение об ошибке) тогда,
когда Excel
не может подобрать такое значение для
изменяе­мого параметра, чтобы указанная
формула возвратила заданное вами
значение.
Такое же сообщение появится, если в
поле Значение
введе­но экстремально маленькое или
экстремально большое число. Чтобы
исправить эту ошибку, сначала в диалоговом
окне Результат
подбора параметра щелкните
на кнопке Отмена,
данное окно закроется. Затем снова
выберите команду Подбор
параметра
и в поле Значение
диалогового
окна Подбор
параметра
введите другое число.

Поиск
решения

Средство
Поиск
решения
позволяет находить для одной формулы
такие значения ее входных переменных,
которые приводили бы к точно заданному
значению, либо минимально или максимально
возможному
значение. Это средство позволяет также
налагать ограничения
на значения любых переменных, от которых
зависит результат вычисления
формулы.

Назначение
средства «Поиск решения»

Если
говорить упрощенно, то средство Поиск
решения
путем изменения
значений в заданных ячейках (такие
ячейки называются изменяемыми
ячейками) добивается
того, чтобы в ячейке с формулой
(называется целевой
ячейкой) было
или определенное (заданное вами)
значение, либо чтобы эта формула
принимала минимально или максимально
возможное значение.
Можно также наложить ограничения на
изменяемые значения, причем эти
ограничения могут быть как прямыми
(например, значения не должны выходить
из определенного интервала), так и
опосредованными,
когда несколько изменяемых значений
связаны каким-либо соотношением и
ограничение налагается
на это соотношение.

Для
примера рассмотрим задачу вычисления
оптимальных цен и
количеств театральных билетов разной
категории таким образом, чтобы
стоимость всех проданных билетов
достигала определенной величины.
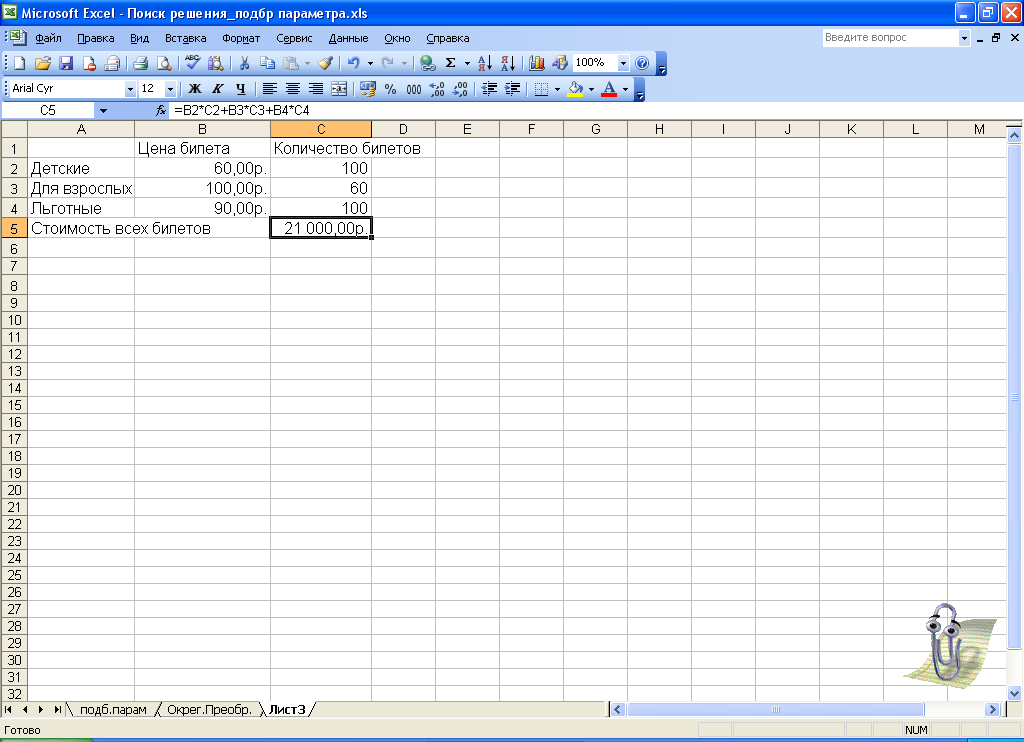
В
театре имеются билеты трех категорий:
детские, для взрослых и льготные (рис.
4.1).

В
целевой ячейке В6 подсчитывается сумма
стоимостей билетов всех категорий
(для каждой категории билетов их
стоимость подсчитыва­ется как
произведение количества билетов и их
цены).

Рис.
4.1.
Рабочий
лист для поиска оптимальной цены
театральных билетов

В
главе 1 при использовании средства
Подбор
параметра за
один раз
мы могли изменять значение только одной
переменной: значение
цены или количество билетов одной
категории. Средство Поиск
решения также
может изменять значения только одной
переменной (т.е.
может работать в режиме подбора
параметра). Однако, чтобы оценить
гибкость и мощь этого средства, следует
использовать его для
изменения нескольких переменных. Кроме
того, это средство мо­жет
добиться от целевой ячейки (точнее, от
формулы, содержащейся в
этой ячейке) не только определенного
заранее значения, но и максимально
или минимально возможного (для этой
формулы) значения.

Кроме
того, подчеркнем еще раз, в отличие от
средства Подбор
параметра
средство Поиск
решения позволяет
налагать разнообразные
ограничения на значения изменяемых
переменных. Например, Поиск
решения может
найти, сколько необходимо продать
театральных
билетов для того, чтобы в кассе оказалось
ровно 24 тыс. руб., при выполнении
следующих ограничений.

• Цена
  детских билетов постоянна и равна 60
  руб.

• Цена
  билетов для взрослых постоянна и равна
  100 руб.

• Цена
  льготных билетов постоянна и равна 90
  руб.

• Билетов
  каждой категории можно продать не
  более 100 шт.

• В
  театре может быть аншлаг, но «лишних
  билетиков» нет.

Поиск
решения немедленно
найдет решение этой задачи: для того,
чтобы
в кассе оказалось ровно 24 тыс. руб.,
необходимо продать 100
детских, 90 для взрослых и 100 льготных
билетов. Поиск
решения по
специальному алгоритму перебирает
возможные комбинации зна­чений
количеств билетов разной категории
для того, чтобы найти искомое
решение.

Другой
пример решения задачи с ограничениями
показан на рис.
4.2. Здесь некий завод производит три
вида изделий, но может производить
в смену суммарно не более 300 изделий.
Необходимо определить при этом
ограничении, а также при условии, что
должно производиться
не менее 30 шт. любого изделия, количество
выпуска­емых изделий таким образом,
чтобы получить максимальный доход.
Ответ,
который дает Поиск решения, показан на
том же рис. 4.2.

Рис.
4.2.
Определение оптимальной структуры
производства

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Нет такого требования, а есть требования, которое я уже публиковал:
Для поиска решения формула целевой ячейки обязательно должна зависеть от значений изменяемых надстройкой ячеек
У Вас следующие ошибки:
1. Нет формул в столбце G, а должны быть.
2. Неправильно записаны 4 нижних ограничения (см. методичку)
Чтобы исключить опечатки лучше использовать именно те ячейки, которые приведены в методичке.
Перед началом расчета нужно задать начальные значения количества бумаг в портфеле (единичное по методичке)
Эволюционный метод решения можно продолжить после сообщения о достижении максимального времени и остановить в любой момент по ESC.
Текущее значение отображается в статусной строке — посматривайте на него и остановите, когда значение будет достаточно оптимальным (можно сравнивать с тем, что в методичке). В приложении — исправленный вариант с результатом, лучшим (5.02%), чем в методичке (4.73%). С Вас — оценка не ниже 5.02 за лабораторную

Что значит содержимое ячейки целевой функции должно быть формулой

Если в ячейку Excel введена формула, содержащая ссылку на эту же самую ячейку (может быть и не напрямую, а опосредованно — через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). На практике к циклическим ссылкам прибегают, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя ее устранения. Excel не может провести вычисления, так как циклические ссылки порождают бесконечное количество вычислений. Есть два выхода из этой ситуации: устранить циклические ссылки или допустить вычисления по формулам с циклическими ссылками (в последнем случае число повторений цикла должно быть конечным).

Рассмотрим задачу нахождения корня уравнения методом Ньютона с использованием циклических ссылок. Возьмем для примера квадратное уравнение: х 2 — 5х + 6=0, графическое представление которого приведено на рис. 8. Найти корень этого (и любого другого) уравнения можно, используя всего одну ячейку Excel.

Для включения режима циклических вычислений в меню Сервис/Параметры/вкладка Вычисления включаем флажок Итерации, при необходимости изменяем число повторений цикла в поле Предельное число итераций и точность вычислений в поле Относительная погрешность (по умолчанию их значения равны 100 и 0,0001 соответственно). Кроме этих установок выбираем вариант ведения вычислений: автоматически или вручную. При автоматическом вычислении Excel выдает сразу конечный результат, при вычислениях, производимых вручную, можно наблюдать результат каждой итерации.

Рис. 8. График функции

Выберем произвольную ячейку, присвоим ей новое имя, скажем — Х, и введем в нее рекуррентную формулу, задающую вычисления по методу Ньютона:

где F и F1 задают соответственно выражения для вычисления значений функции и ее производной. Для нашего квадратного уравнения после ввода формулы в ячейке появится значение 2, соответствующее одному из корней уравнения (рис. 8). В нашем случае начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке Х и равного нулю. А как получить второй корень? Обычно это можно сделать изменением начального приближения. Решать проблему задания начальных установок в каждом случае можно по-разному. Мы продемонстрируем один прием, основанный на использовании функции ЕСЛИ. С целью повышения наглядности вычислений ячейкам были присвоены содержательные имена (рис. 9).

• В ячейку Хнач (В4) заносим начальное приближение — 5.
• В ячейку Хтекущ (С4) записываем формулу:
  =ЕСЛИ(Хтекущ=0;Хнач; Хтекущ-(Хтекущ^2-5*Хтекущ+6)/(2*Хтекущ-5)).
• В ячейку D4 помещаем формулу, задающую вычисление значения функции в точке Хтекущ, что позволит следить за процессом решения.
• Заметьте, что на первом шаге вычислений в ячейку Хтекущ будет помещено начальное значение, а затем уже начнется счет по формуле на последующих шагах.
• Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного
  
  

  Рис. 9. Определение начальных установок

  значения. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул). Щелчок по кнопке (нажатие клавиши) Enter запустит вычисления с новым начальным приближением.

2.2. Подбор параметра

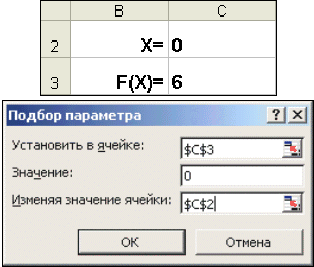
Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Возьмем в качестве примера все то же квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:

• В ячейку С3 (рис. 10) введем формулу для вычисления значения функции,
  
  

  Рис. 10. Окно диалога Подбор параметра

  стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

• В окне диалога Подбор параметра (рис. 10) в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
• После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.

Вернемся к примеру. Опять возникает вопрос: как получить второй корень? Как и в предыдущем случае необходимо задать начальное приближение. Это можно сделать следующим образом (рис. 11,а):

• В ячейку Х (С2) вводим начальное приближение.
• В ячейку Х_i (С3) вводим формулу для вычисления очередного приближения к корню, т.е.
  =X-(X^2-5*X+6)/(2*X-5).
• В ячейку С4 поместим формулу, задающую вычисление значения функции, стоящей в левой части исходного уравнения, в точке Х_i.
• После этого выбираем команду Подбор параметра, где в качестве изменяемой ячейки принимаем ячейку С2. Результат вычислений изображен на рис. 11,б (в ячейке С2 — конечное значение, а в ячейке С3 — предыдущее).

Однако все это можно сделать и несколько проще. Для того чтобы найти второй корень, достаточно в качестве начального приближения (рис. 10) в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.

2.3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Искомые переменные — ячейки рабочего листа Excel — называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

• найти максимум целевой функции F(х₁, х₂, … , х_n);
• найти минимум целевой функции F(х₁, х₂, … , х_n);
• добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

Рис. 12. Окно диалога Поиск решения

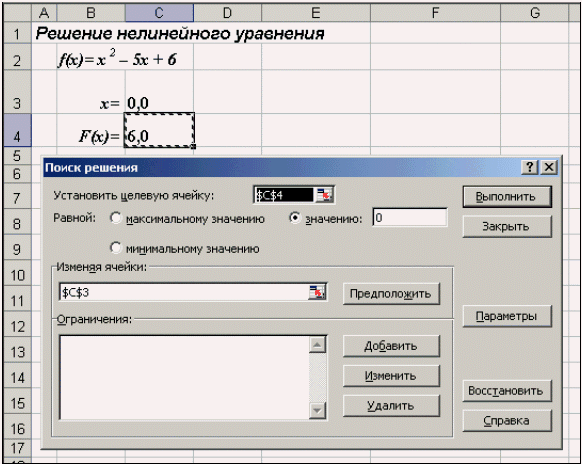
После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:

1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение 8 , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Рис. 13. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

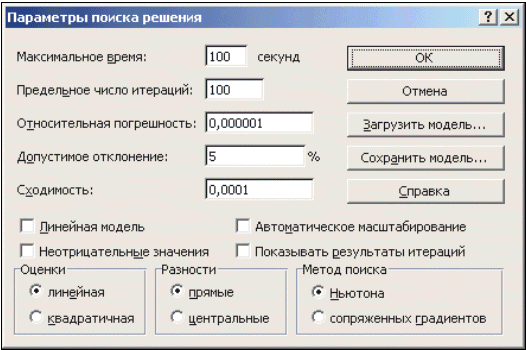
Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):

Рис. 14. Настройка параметров Решателя

• Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).
• Предельное число итераций — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.
• Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).
• Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.
• Сходимость — когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.
• Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Это ускоряет процесс поиска решения.
• Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.
• Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.
• Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.
• Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
• Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.
• Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.

Сохранить модель поиска решения можно следующими способами:

1. при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;
2. если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;
3. еще один способ сохранения параметров поиска — сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.

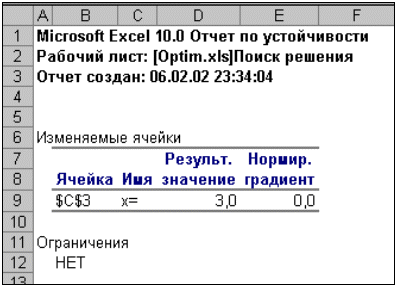Рис. 15. Отчет по устойчивости

Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

Рис. 16. Отчет по результатам

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй — значения искомых переменных, полученные в результате решения задачи, в третьей — результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы — это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение — это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение — это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Подбор параметра. Поиск решения.

Подбор параметра 1. Подбор параметров для нахождения значения, приводящего к требуемому результату. 2. Надстройка Поиск решения для расчета оптимальной величины по нескольким переменным и ограничениям; 3. Диспетчер сценариев для создания и оценки наборов сценариев «что – если» с несколькими вариантами исходных данных.

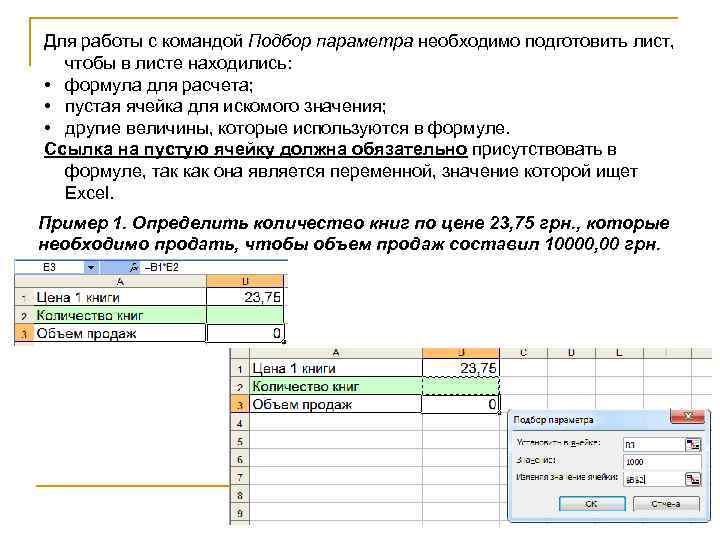
Использование средства Подбор параметров: — находит такое значение параметра, которое обеспечит требуемое значение, вычисленное по формуле, зависящей от этого параметра. — применяется тогда, когда вы знаете значение, которое должна возвращать формула, но не знаете входное значение для формулы, обеспечивающее желаемый результат вычислений. Чтобы применить средство Подбор параметра, на вкладке Данные в группе Работа с данными нажмите кнопку Анализ «что-если» и выберите Подбор параметра (рис. 1). Рис. 1. Открытие средства Подбор параметра

Для работы с командой Подбор параметра необходимо подготовить лист, чтобы в листе находились: • формула для расчета; • пустая ячейка для искомого значения; • другие величины, которые используются в формуле. Ссылка на пустую ячейку должна обязательно присутствовать в формуле, так как она является переменной, значение которой ищет Excel. Пример 1. Определить количество книг по цене 23, 75 грн. , которые необходимо продать, чтобы объем продаж составил 10000, 00 грн.

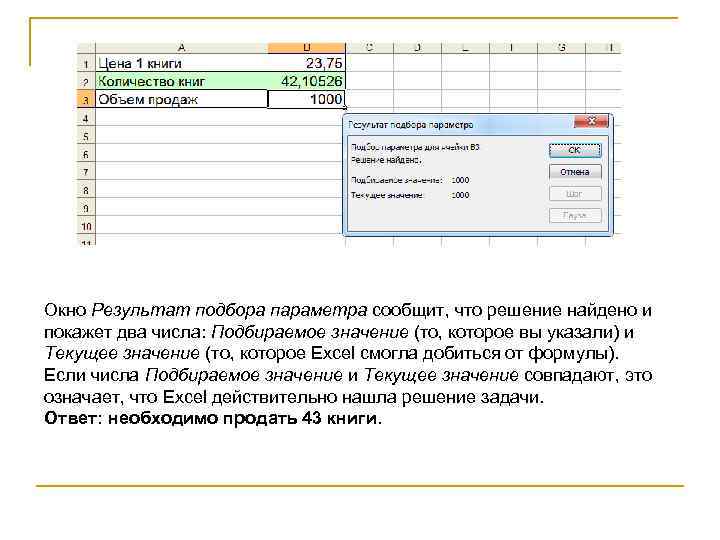
Окно Результат подбора параметра сообщит, что решение найдено и покажет два числа: Подбираемое значение (то, которое вы указали) и Текущее значение (то, которое Excel смогла добиться от формулы). Если числа Подбираемое значение и Текущее значение совпадают, это означает, что Excel действительно нашла решение задачи. Ответ: необходимо продать 43 книги.

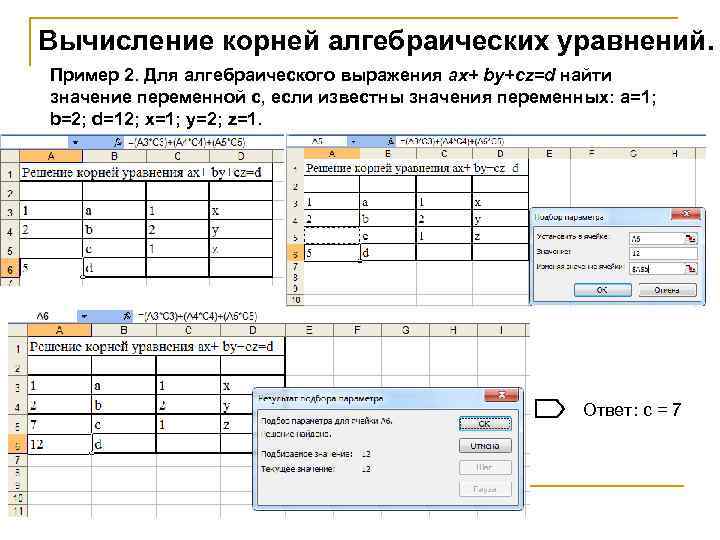
Вычисление корней алгебраических уравнений. Пример 2. Для алгебраического выражения ax+ by+cz=d найти значение переменной с, если известны значения переменных: а=1; b=2; d=12; x=1; y=2; z=1. Ответ: с = 7

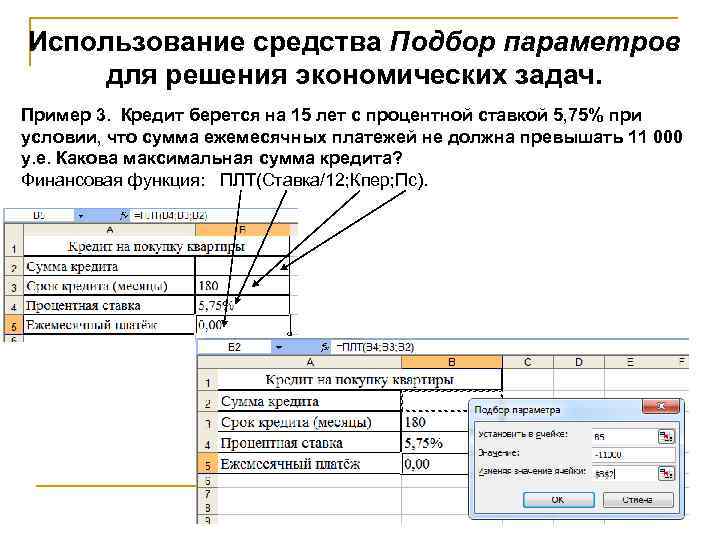
Использование средства Подбор параметров для решения экономических задач. Пример 3. Кредит берется на 15 лет с процентной ставкой 5, 75% при условии, что сумма ежемесячных платежей не должна превышать 11 000 у. е. Какова максимальная сумма кредита? Финансовая функция: ПЛТ(Ставка/12; Кпер; Пс).

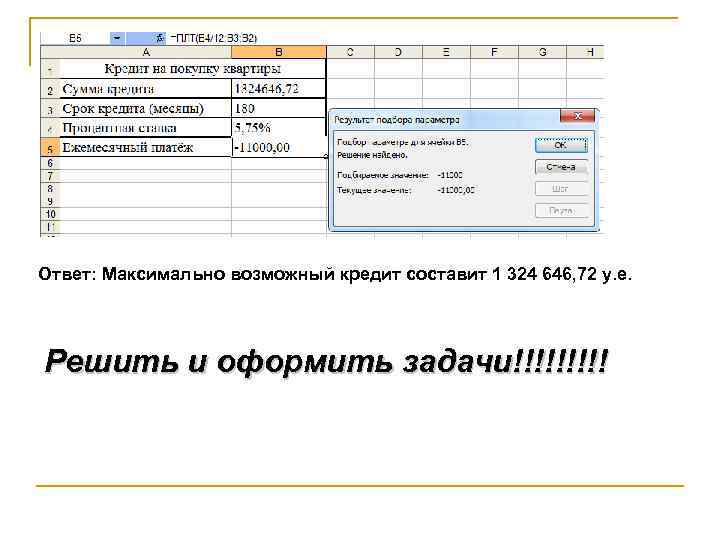
Ответ: Максимально возможный кредит составит 1 324 646, 72 у. е. Решить и оформить задачи!!!!!

Ошибки при работе со средством Подбор параметра Ячейка должна содержать формулу. Это сообщение об ошибке появляется тогда, когда ячейка, адрес которой указан в поле ввода Установить в ячейке диалогового окна Подбор параметра, не содержит формулы. Чаще всего в этом поле введён адрес ячейки, который должен быть указан в поле ввода Изменяя значение ячейки. Закройте сообщение об ошибке, а затем введите в поле Установить в ячейке адрес ячейки, содержащей формулу. Введено недопустимое значение. Это сообщение появляется тогда, когда в поле ввода Значение кроме числа введены еще какие-то символы, которые Excel не может распознать как числа. Закройте сообщение об ошибке, а затем введите в поле Значение правильное число (целое или десятичное). К числу можно добавить знак денежной единицы или процента. Ячейка должна содержать значение. Это сообщение появляется тогда, когда ячейка, адрес которой указан в поле ввода Изменяя значение ячейки, не содержит числового значения (а содержит, например, текст или формулу). Чтобы исправить эту ошибку, введите в поле Изменяя значение ячейки адрес ячейки, содержащей числовое значение.

Введенный текст не является правильной ссылкой или именем. Это сообщение появляется тогда, когда в поле ввода Установить в ячейке или в поле ввода Изменяя значение ячейки введено нечто, что Excel не может распознать как ссылку на ячейку. Чаще всего такая ошибка возникает тогда, когда адрес ячейки вводится вручную, а не указывается путем щелчка мыши на нужной ячейке. Чтобы исправить эту ошибку, введите в поле ввода правильный адрес ячейки. Решение не найдено. Это сообщение появляется в диалоговом окне Результат подбора параметра (а не как сообщение об ошибке) тогда, когда Excel не может подобрать такое значение для изменяемого параметра, чтобы указанная формула возвратила заданное значение. Такое же сообщение появится, если в поле Значение введено экстремально маленькое или экстремально большое число. Чтобы исправить эту ошибку, сначала в диалоговом окне Результат подбора параметра щелкните на кнопке Отмена, данное окно закроется. Затем снова вызовите окно Подбор параметра и в поле Значение введите другое число.

Поиск решения Для решения сложных задач, требующих применения линейного и нелинейного программирования, а также методов исследования операций применяется надстройка — Поиск решения. Чтобы использовать надстройку Поиск решения не обязательно знать методы программирования и исследования операций, но необходимо определять, какие задачи можно решать этими методами. Общие свойства для задач, решаемых с помощью Поиск решения: 1. Существует единственная целевая ячейка, содержащая формулу, значение которой должно быть максимальным, минимальным или равным, какому-то конкретному значению. 2. Формула в этой целевой ячейке содержит ссылки на ряд изменяемых ячеек. Поиск решения заключается в том, чтобы подобрать такие значения переменных в изменяемых ячейках, которые бы обеспечили оптимальное значение для формулы в целевой ячейке. 3. Может быть задано некоторое количество ограничений — условий или соотношений, которым должны удовлетворять некоторые из изменяемых ячеек.

Терминология: Целевая ячейка – ячейка с формулой, в которой Поиск решения установит заданное значение или для которой найдет минимально или максимально возможные значения. Целевая функция – это термин из теории оптимизации, описывающий цель, которую мы хотим достичь, решая данную задачу (и используя для этого Поиск решения). Здесь «цель» заключается в том, чтобы формула в целевой ячейке достигла определенного значения. Изменяемые ячейки – ячейки, значения в которых будет варьировать Поиск решения для того, чтобы достичь требуемого значения целевой функции. Ограничения – условия, налагаемые на возможные значения изменяемых ячеек. Модель – совокупность адресов целевой и изменяемых ячеек, а также всех ограничений, используемых средством Поиск решения для решения текущей задачи, которые оно сохранило как единое целое.

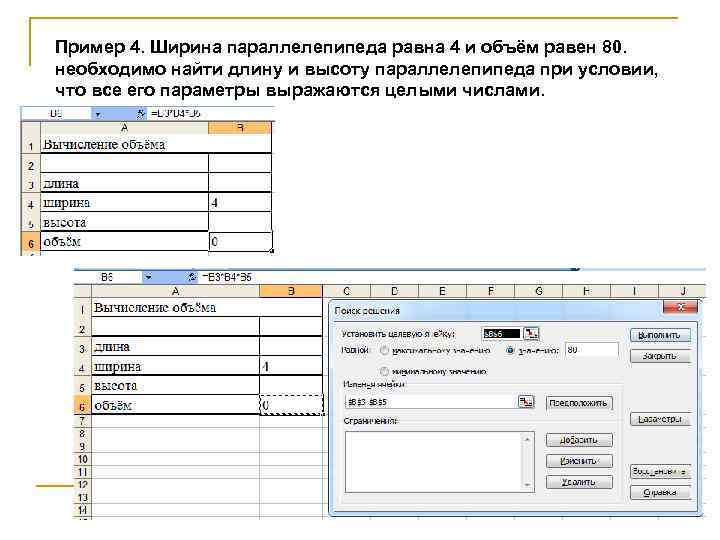
Пример 4. Ширина параллелепипеда равна 4 и объём равен 80. необходимо найти длину и высоту параллелепипеда при условии, что все его параметры выражаются целыми числами.

С помощью Excel можно выполнять почти какого-угодно порядка: вычислять и даже программировать действия компьютера. Все потому, что в функционал заложены функции и формулы. Но иногда пользователю приходится сталкиваться с ошибками при их вводе. Особенно часто они возникают, когда человек пытается ввести формулу вручную. Если пользователь опытный, такая проблема встречается не очень часто, поскольку он уже знает, какой синтаксис правильный, а также довольно внимательный. Но даже профессионалы могут допускать ошибки.

Часто мы не понимаем, почему они возникают. И профессионалы тоже могут не знать, какие причины. Он может понимать, что означает тот или иной код ошибки, но найти конкретное место в формуле не может. Но для профессионала это не проблема, поскольку он знает, как находить ошибки методами самого Excel. Сегодня мы более детально разберемся в причинах самых распространенных ошибок при вводе формул в Excel и разберем методы решения этой проблемы. Тем самым мы значительно ближе будем к профессионалам. Ну что же, начнем?

Изменение формата ячеек Excel

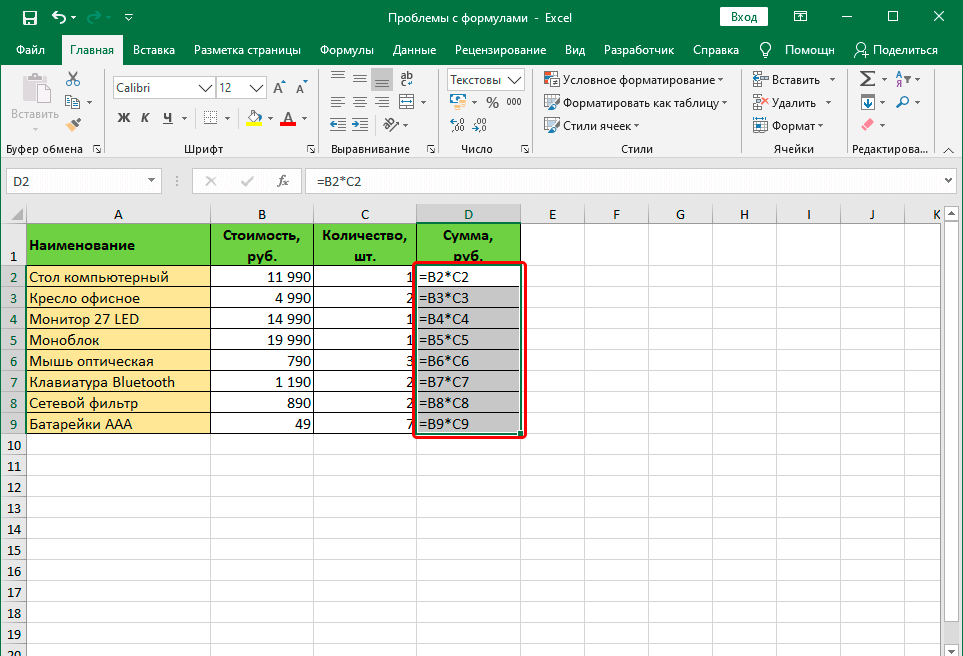
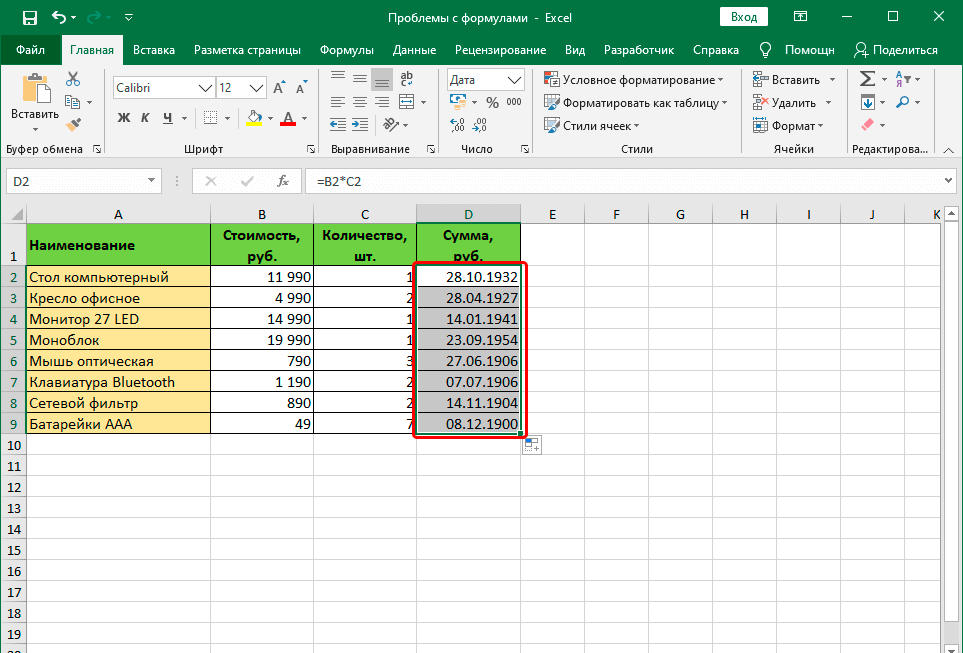
Довольно нередкая причина того, почему у человека появляется неудача в ходе записи формул, заключается в том, что он неверно выбрал формат ячеек, на какие она ссылается. Так, если в ней поставили формат «текст», то вместо итогового значения перед нами будет просто показана формула в виде текстовой строки.

Есть случаи, когда формат считается правильно, но отображается неверно. Причина этого явления — также ошибочно выбранный формат. Эта проблема может появиться и сама собой, через глюки в работе программы. Как ни странно, человеческий фактор влияет и на работу компьютера, который не является человеком. Но это уже лирическое отступление.

Конечно, в таком случае следует выставить правильный формат. Для этого нужно следовать таким шагам:

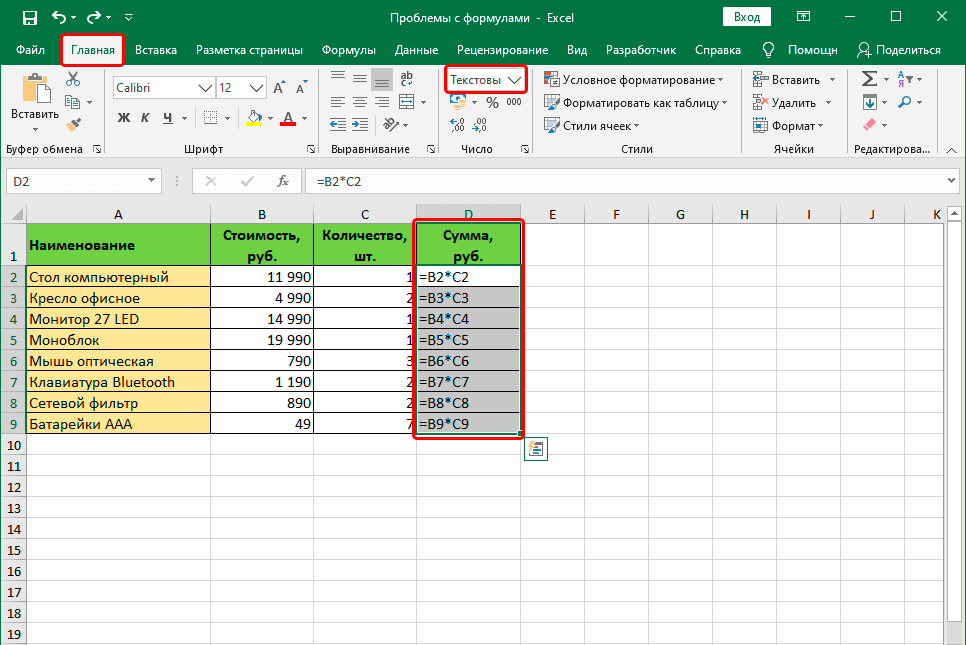
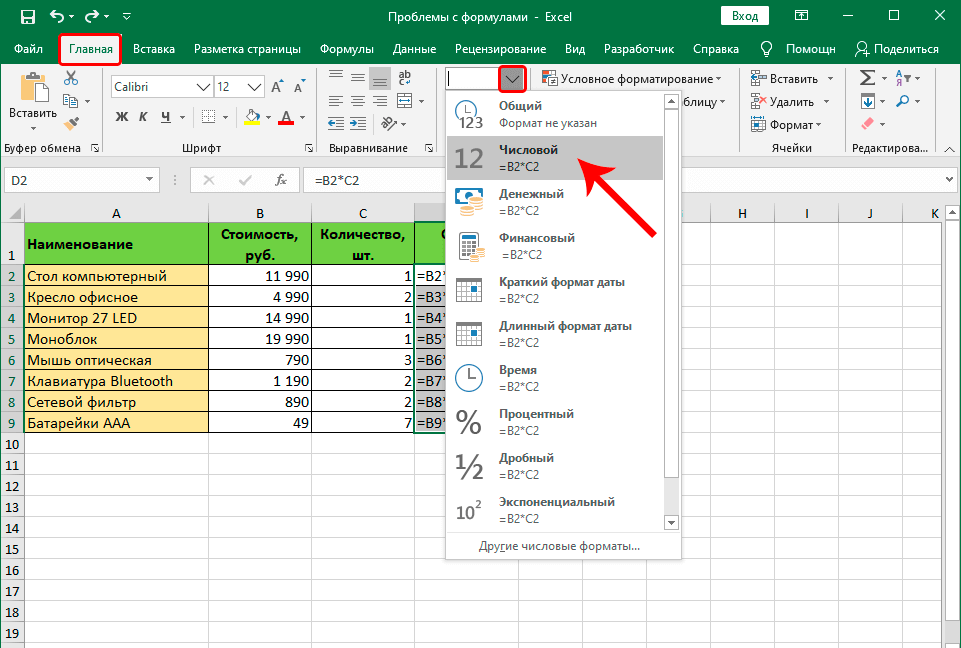
1. Выделить ячейку и перейти на вкладку «Главная» на ленте. После этого перемещаем курсор мыши в группу «число». Здесь также есть поле, в котором демонстрируется формат, в данный момент присвоенные ячейке.
2. Нужно нажать на стрелку вниз возле этого поля. После этого появится список с разными форматами ячеек. Нужно выбрать тот, который соответствует тому, который нужно применять в конкретной формуле. После этого делается клик по выбранному варианту.

Есть еще один инструмент, настройки которого более широки. Чтобы его применить, необходимо выполнять следующую инструкцию:

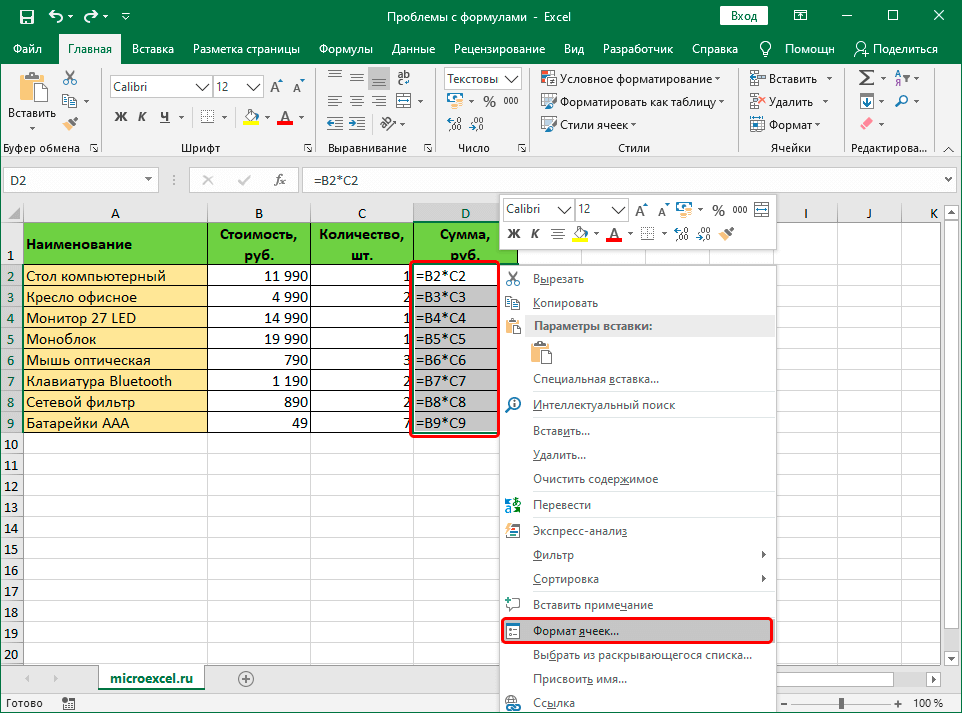
1. Определить, нам нужно изменить формат одной ячейки или нескольких. После этого выбираем ту, которая нам подходит (или целый диапазон выделяем), после чего делаем правый клик по ней (ним). Далее ищем в появившемся перечне пункт «Формат ячеек». Задача может быть существенно упрощена, если пользователь нажмет сочетание Ctrl+1.

1. После этого появляется диалоговое окно, в котором по умолчанию будет открыта вкладка «Число». Важно убедиться, что открыта именно она. После этого следует обратить ваш взор на список в левой части окна. Там находится перечень доступных форматов ячеек. Нужно выбрать тот, который подходит в конкретной ситуации и нажать ОК.

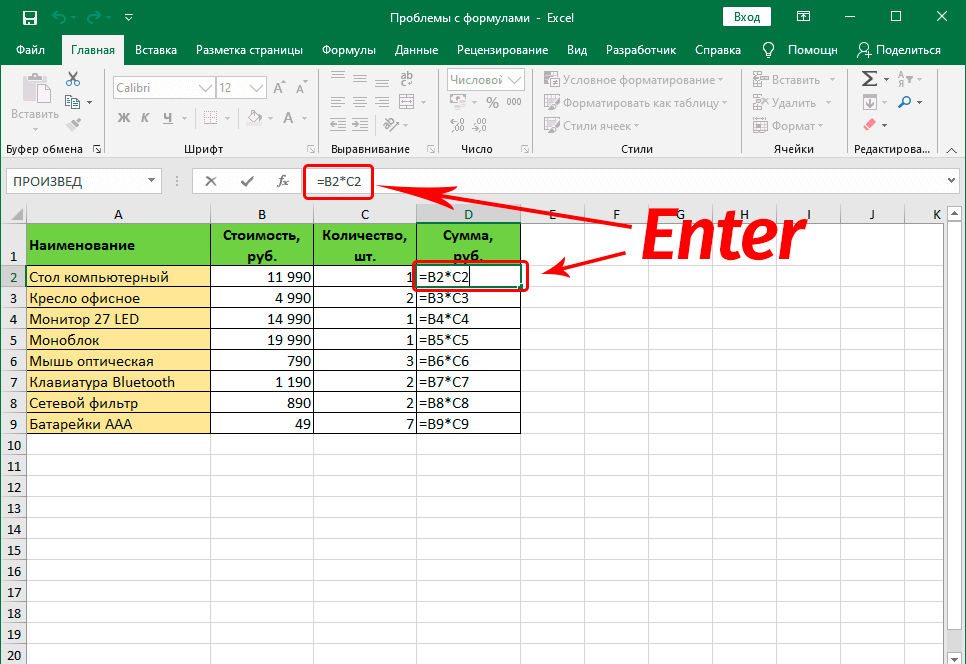
Для сохранения полученных изменений необходимо воспользоваться функцией редактирования для каждой ячейки с ошибкой при вводе формулы. После того, как мы найдем тот элемент, который нужен, следует отредактировать с помощью клавиши F2 или выполнения двойного клика по соответствующей ячейке. Также внесение изменений возможно с помощью левого щелчка мыши в строке формул. После внесения всех изменений в документ нужно подтвердить свои действия путем нажатия клавиши Enter.

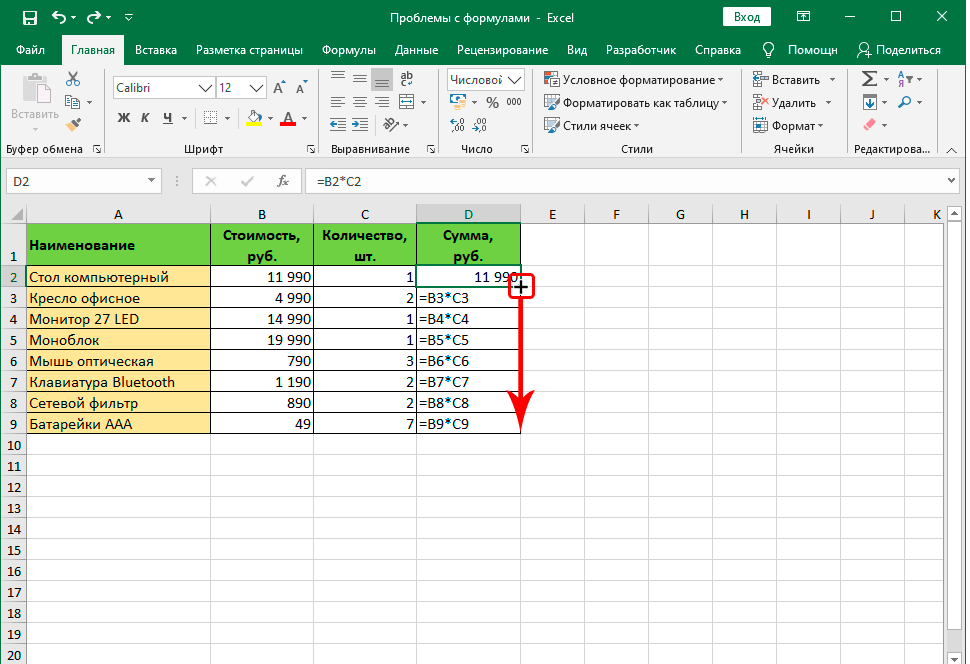
Внимание. При наличии большого количества информации, последний шаг может потребовать очень много времени. В этом случае можно упростить задачу, применив маркер автозаполнения. Правда, этим методом можно воспользоваться только в одном случае. Главное — требование — в каждой ячейке должна применяться та же формула.

Что следует делать на практике?

1. Выделяем ячейку, которая расположена в самом верху диапазона.
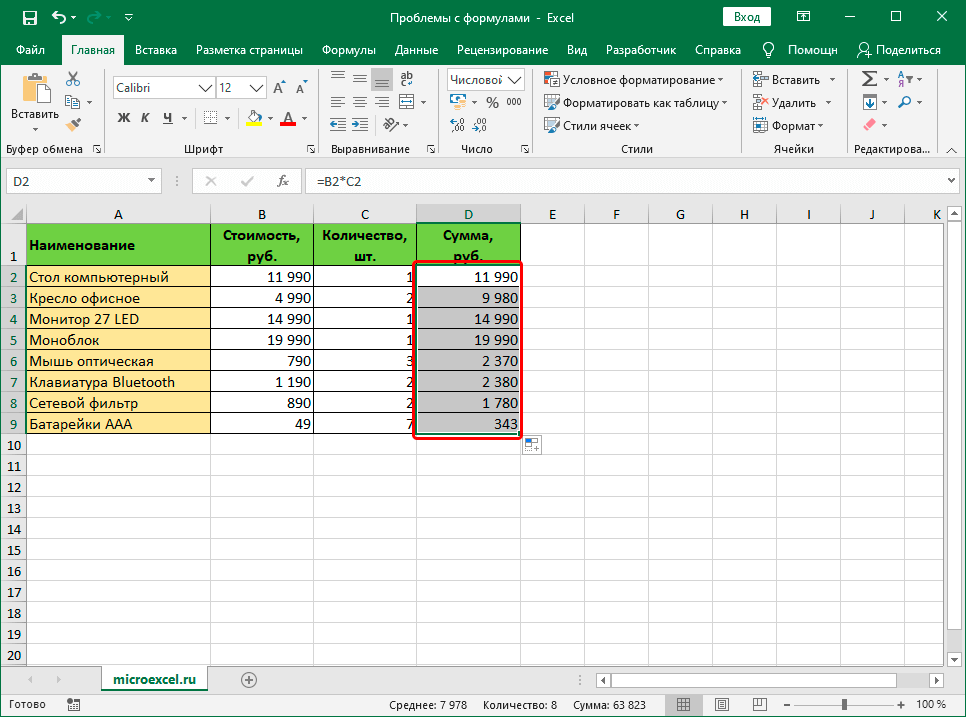
2. Наводим курсор на ее правую нижнюю часть (то есть, на угол), убеждаемся в том, что появился знак плюса черного цвета, нажимаем левую кнопку, зажимаем ее и перемещаем курсор до того места, где должен закончиться этот диапазон.

После выполнения этих операций перед нашим взором стоит готовый столбец, который был сгенерирован почти без нашего участия.

Отключение режима “Показать формулы” в Excel

Случаются ситуации, когда пользователь не обнаруживает результатов, хотя он их ждал после выполнения операций функцией. Вместо них отображаются только формулы. Причина этого может крыться в том, что включена демонстрация формул, и естественно, нам нужно ее отключить, чтобы увидеть итог вычислений. Выполняем следующие действия:

1. Находим в главном меню вкладку «Формулы». Немного ниже и правее нее находится группа инструментов «Зависимость формул», в которой находится кнопка «Показать формулы». Нужно сделать один левый клик мышью при условии, что эта функция активирована.

1. После этого в каждой ячейке теперь можно увидеть итоги вычислений. Естественно, это может повлиять на границы колонок, но в этом нет никакой супер страшной проблемы. Этот вопрос решается буквально в несколько кликов.

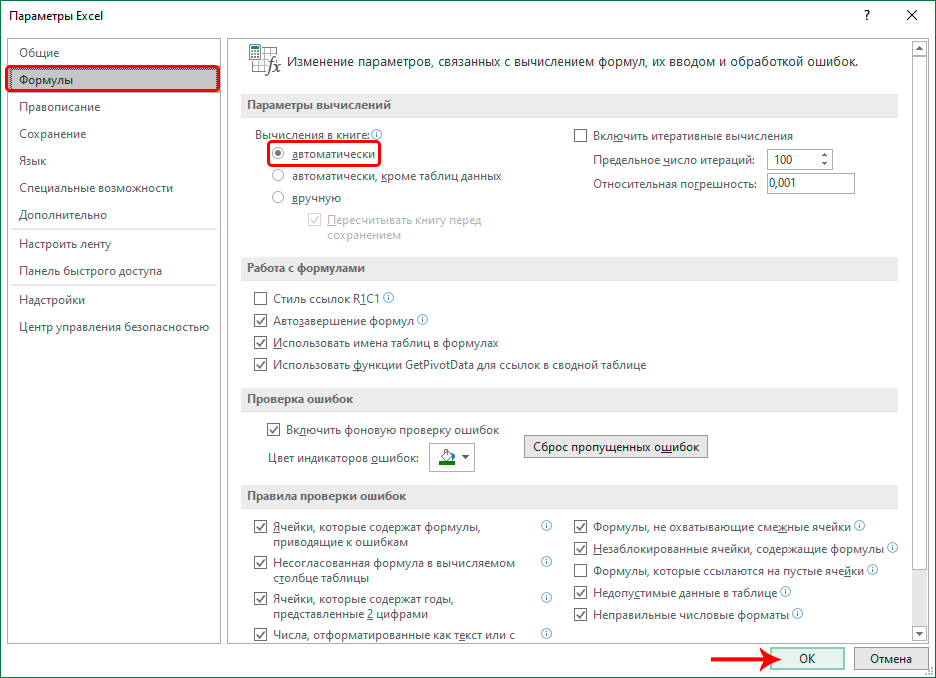
Активизация автоматического пересчета формул в Excel

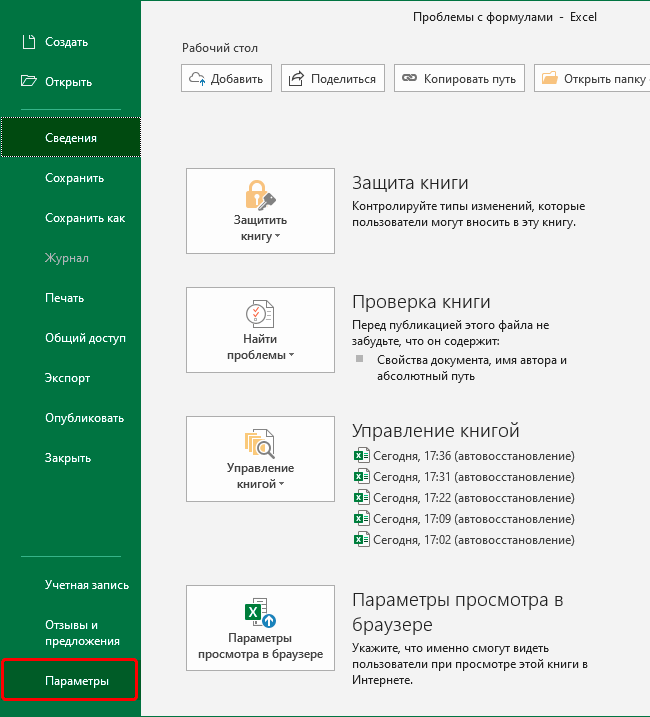
Время от времени появляются ситуации, когда результат формулы не меняется, если в одной из ячеек, данные которой использовались для подсчета, происходит коррекция значений. Чтобы исправить эту проблему, необходимо воспользоваться меню настроек. Следуйте этим действиям:

1. Переходим в меню «Файл».
2. После этого ищем раздел «Параметры» и переходим в него.
3. Далее мы увидим окно. В списке справа находится большое количество различных разделов, но нас интересует «Формулы». После клика мы увидим, что правая часть окна изменилась. Переходим в группу «Параметры вычислений», где ставим флажок возле функции «автоматически». После того, как действия будут выполнены, нам нужно нажать кнопку ОК.

Теперь можно отдыхать, поскольку проблема решена. Все вычисления осуществляются автоматически. И если какое-то из значений вдруг изменяется, программа автоматически его пересчитывает.

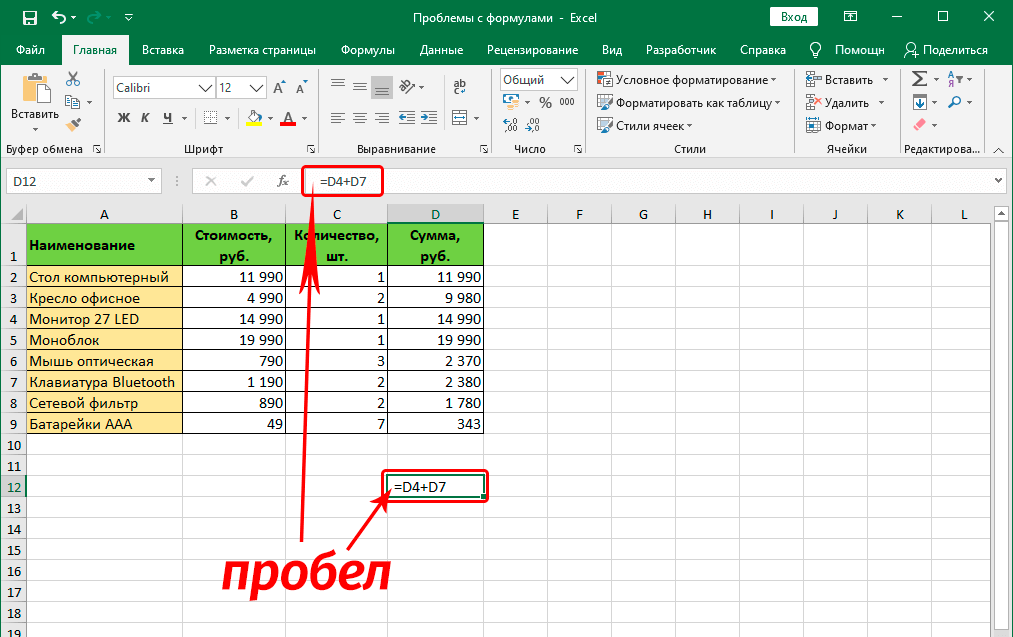
Исправление ошибок в формулах

Бывают ситуации, когда человек допускает ошибку при вводе формулы. В этом случае программа будет просто ее определять, как простое значение в текстовом формате. То есть, и расчетов также не будет. Так, самой распространенной ошибкой является ситуация, когда перед вводом знака «равно» ставится пробел. Здесь важно помнить, что перед знаком = не должно быть никаких пробелов, и он всегда должен располагаться перед формулой.

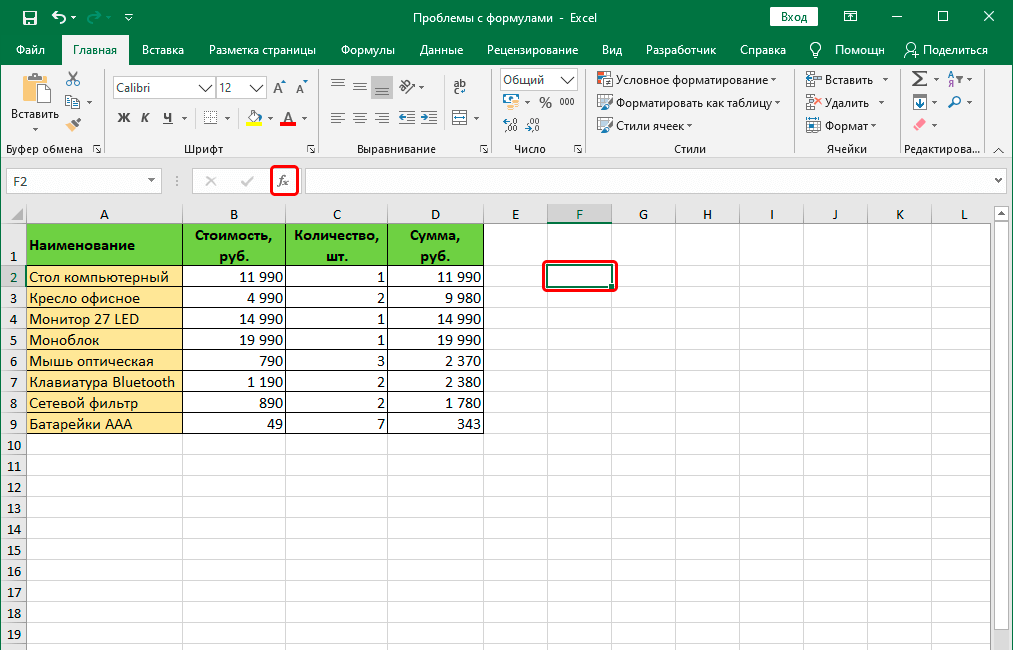
Кроме этого, нередко ошибки появляются в синтаксисе функций. Причина этого проста — не все они просты для заполнения обычными людьми. Особенно это касается ситуаций, когда применяется сразу несколько аргументов. Поэтому ручной ввод формул рекомендуется лишь если пользователь опытный, и в таком случае синтаксис нужно тщательно перепроверять. Для того, чтобы сделать ввод функций более простым, был создан Мастер функций, который вызывается путем нажатия клавиши fx слева от строки ввода формулы.

Для обеспечения работоспособности формулы необходимо тщательно проверять ее перед вводом. В том числе, необходимо убедиться в том, что в ней нигде не стоят знаки, которые не видимы невооруженным глазом. В нашем случае таким знаком служил пробел.

Время от времени лучше удалить формулу, где стоят некоторые непечатные символы или ее синтаксис написан уж откровенно неправильно, чем искать ошибку и ее исправлять. Это же касается не только названия формулы, но и ее функций. О том, что при вводе формулы была допущена ошибка, Excel сообщит определенным кодом. Каждый из кодов имеет конкретное значение. Давайте перечислим наиболее распространенные из них.

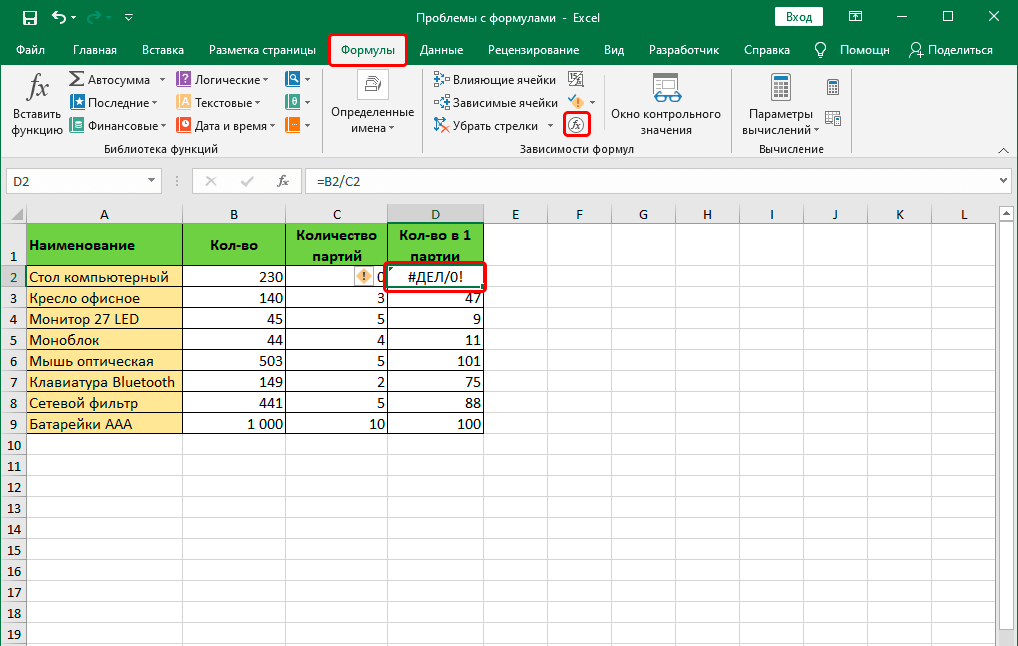
Если хотя бы одна из этих ошибок появляется, то нужно проверить, правильно ли заполнена информация в аргументах этой функции. После этого осуществляется проверка самой формулы и то, есть ли в ней ошибки. Особенно нужно акцентировать внимание на тех из них, которые не соответствуют законам математики. Например, очень частая проблема — деление на ноль. Нередко она возникает случайно. Просто в результате вычисления определенного значения функцией, которая входит в состав формулы и служит аргументом для функции более высокого порядка, появляется число ноль. В результате, формула выдает ошибку #ДЕЛ/0.

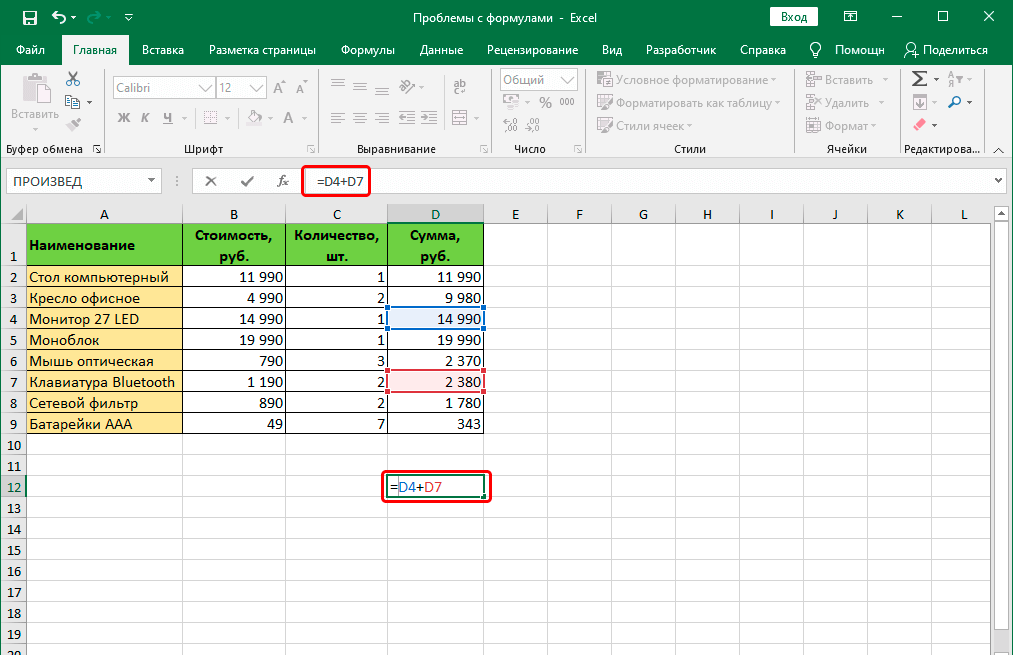
Бывают и ситуации потруднее, когда точно сказать, где кроется ошибка, нельзя. Если приходится иметь дело со сложными функциями, то в таком случае нужно использовать специальные инструменты проверки. Следуйте этой инструкции:

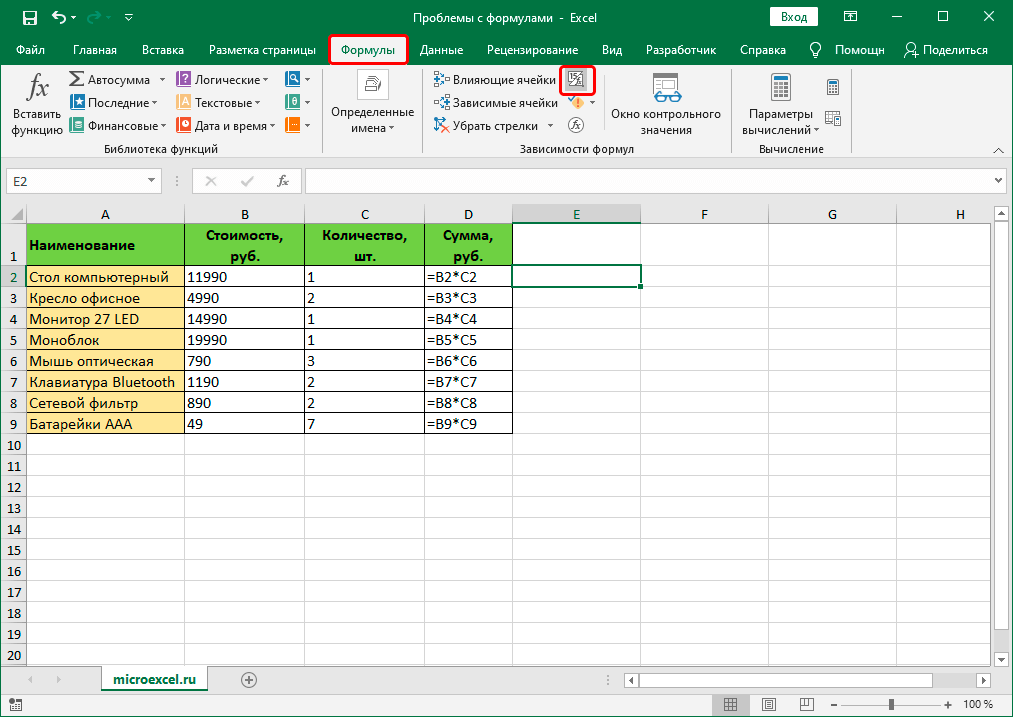
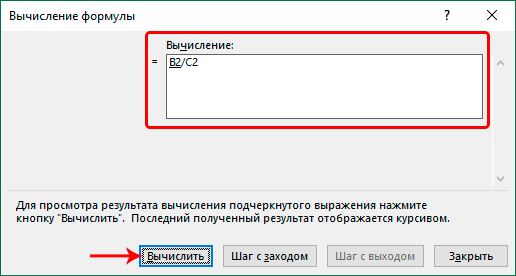
1. Выделяем ту ячейку, в которой есть ошибочная формула. Далее переходим во вкладку «Формулы». Там нужно найти инструмент «Зависимости формул» — «Вычислить формулу».
2. Перед глазами пользователя появится диалоговое окно. В нем детально будет описано, как осуществлять отчет правильно. Чтобы решить проблему, необходимо нажать кнопку «Вычислить». После этого функция будет последовательно проверяться на каждом шагу. Поэтому кнопку нужно нажать несколько раз. Таким образом можно отследить, на каком шагу возникла проблема и оперативно ее решить.

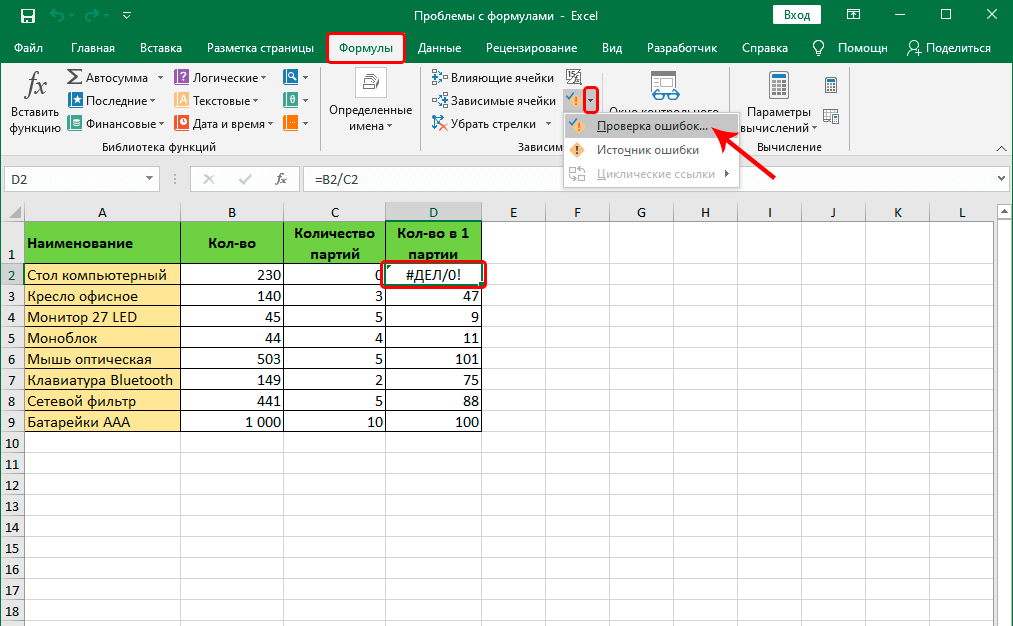
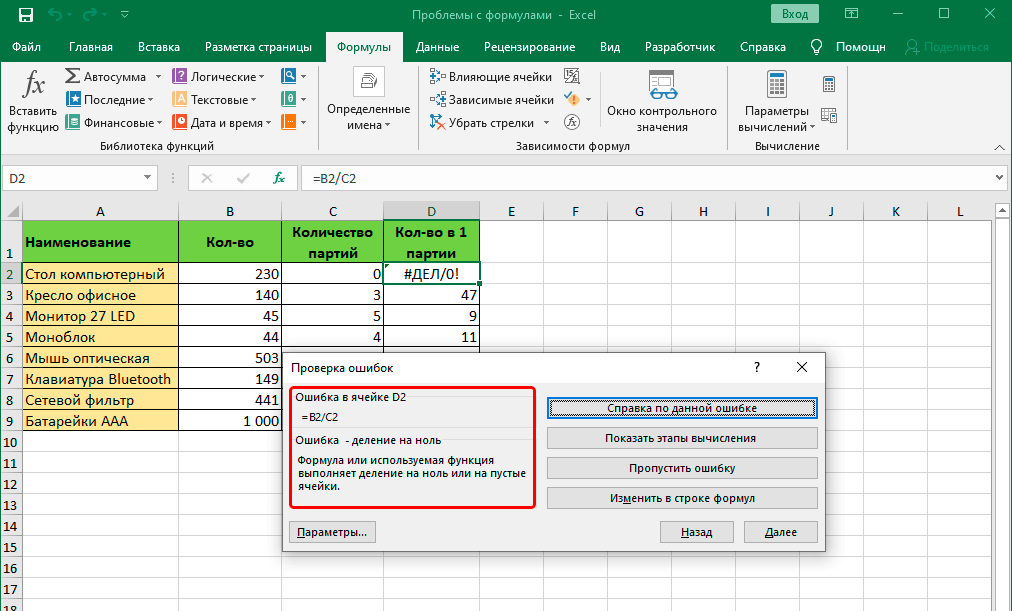
Есть еще один способ определения причин неполадок при работе с формулами. Называется этот инструмент «Проверка ошибок». Его можно найти в том же блоке, что и предыдущий.

После того, как мы нажмем на соответствующую кнопку, появится окно. В нем будет информация о том, что вызвало ошибку, а также будут приведены рекомендации по исправлению сложившейся ситуации.

Чтобы исправить проблему, необходимо нажать на кнопку «Изменить в строке формул». После этого формула будет работать правильно.

Исправление ошибки в синтаксисе

Надо сказать, что все особенности исправления ошибок в синтаксисе были описаны выше, потому что это частный случай ошибок в формулах. Тем не менее, давайте резюмируем то, что было сказано, поскольку ошибка в синтаксисе — очень частая проблема начинающих пользователей Excel. Для проверки синтаксиса существует два специализированных инструмента: проверка формул и вычисление. Также можно воспользоваться ручным методом проверки. Когда какой лучше использовать?

1. В целом, если формула небольшая, ее можно проверить и самостоятельно. Это не потребует большого количества времени. Также можно без проблем проверять формулы самостоятельно, если их количество небольшое. Дело в том, что при увеличении количества формул увеличивается и количество ошибок при проверке. Мозг загромождается большим количеством информации, пусть и простой для обработки.
2. Если есть большое количество формул или сами формулы довольно большие, лучше воспользоваться специализированным инструментом. Каким именно — решать только вам. Каждый из них подходит, просто один предусматривает выполнение действий более в ручном режиме, а другой — автоматическом.

Настоятельно рекомендуется на досуге потренироваться использовать эти инструменты, чтобы в реальной рабочей ситуации не теряться. Так, в Excel часто делаются отчеты, которые имеют свои дедлайны. И если близко к дедлайну появится ошибка, которую невозможно оперативно исправить, пользователь может столкнуться с большой паникой и завалить весь отчет. Поэтому все навыки, связанные с Excel, нужно доводить до автоматизма перед тем, как использовать их на практике.

Выводы

С ошибками приходится сталкиваться каждому человеку, который пользуется электронными таблицами. Это неотъемлемая часть рабочего процесса. Поэтому умение обрабатывать ошибки — важнейший навык. Выше были перечислены самые распространенные ошибки, с которыми могут сталкиваться пользователи при вводе формул. Кроме того, были описаны методы решения возникающих проблем и приведены ситуации, в которых необходимо использовать каждый из них.