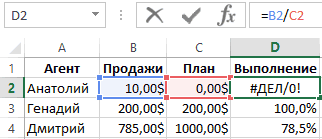
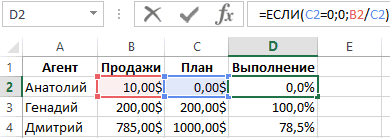
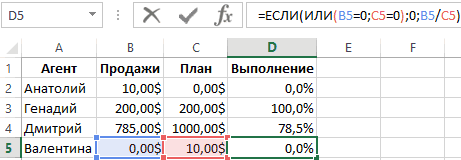
Обработка ошибок увеличивает отказоустойчивость кода, защищая его от потенциальных сбоев, которые могут привести к преждевременному завершению работы.
Прежде чем переходить к обсуждению того, почему обработка исключений так важна, и рассматривать встроенные в Python исключения, важно понять, что есть тонкая грань между понятиями ошибки и исключения.
Ошибку нельзя обработать, а исключения Python обрабатываются при выполнении программы. Ошибка может быть синтаксической, но существует и много видов исключений, которые возникают при выполнении и не останавливают программу сразу же. Ошибка может указывать на критические проблемы, которые приложение и не должно перехватывать, а исключения — состояния, которые стоит попробовать перехватить. Ошибки — вид непроверяемых и невозвратимых ошибок, таких как OutOfMemoryError, которые не стоит пытаться обработать.
Обработка исключений делает код более отказоустойчивым и помогает предотвращать потенциальные проблемы, которые могут привести к преждевременной остановке выполнения. Представьте код, который готов к развертыванию, но все равно прекращает работу из-за исключения. Клиент такой не примет, поэтому стоит заранее обработать конкретные исключения, чтобы избежать неразберихи.
Ошибки могут быть разных видов:
- Синтаксические
- Недостаточно памяти
- Ошибки рекурсии
- Исключения
Разберем их по очереди.
Синтаксические ошибки (SyntaxError)
Синтаксические ошибки часто называют ошибками разбора. Они возникают, когда интерпретатор обнаруживает синтаксическую проблему в коде.
Рассмотрим на примере.
a = 8
b = 10
c = a b
File "", line 3
c = a b
^
SyntaxError: invalid syntax
Стрелка вверху указывает на место, где интерпретатор получил ошибку при попытке исполнения. Знак перед стрелкой указывает на причину проблемы. Для устранения таких фундаментальных ошибок Python будет делать большую часть работы за программиста, выводя название файла и номер строки, где была обнаружена ошибка.
Недостаточно памяти (OutofMemoryError)
Ошибки памяти чаще всего связаны с оперативной памятью компьютера и относятся к структуре данных под названием “Куча” (heap). Если есть крупные объекты (или) ссылки на подобные, то с большой долей вероятности возникнет ошибка OutofMemory. Она может появиться по нескольким причинам:
- Использование 32-битной архитектуры Python (максимальный объем выделенной памяти невысокий, между 2 и 4 ГБ);
- Загрузка файла большого размера;
- Запуск модели машинного обучения/глубокого обучения и много другое;
Обработать ошибку памяти можно с помощью обработки исключений — резервного исключения. Оно используется, когда у интерпретатора заканчивается память и он должен немедленно остановить текущее исполнение. В редких случаях Python вызывает OutofMemoryError, позволяя скрипту каким-то образом перехватить самого себя, остановить ошибку памяти и восстановиться.
Но поскольку Python использует архитектуру управления памятью из языка C (функция malloc()), не факт, что все процессы восстановятся — в некоторых случаях MemoryError приведет к остановке. Следовательно, обрабатывать такие ошибки не рекомендуется, и это не считается хорошей практикой.
Ошибка рекурсии (RecursionError)
Эта ошибка связана со стеком и происходит при вызове функций. Как и предполагает название, ошибка рекурсии возникает, когда внутри друг друга исполняется много методов (один из которых — с бесконечной рекурсией), но это ограничено размером стека.
Все локальные переменные и методы размещаются в стеке. Для каждого вызова метода создается стековый кадр (фрейм), внутрь которого помещаются данные переменной или результат вызова метода. Когда исполнение метода завершается, его элемент удаляется.
Чтобы воспроизвести эту ошибку, определим функцию recursion, которая будет рекурсивной — вызывать сама себя в бесконечном цикле. В результате появится ошибка StackOverflow или ошибка рекурсии, потому что стековый кадр будет заполняться данными метода из каждого вызова, но они не будут освобождаться.
def recursion():
return recursion()
recursion()
---------------------------------------------------------------------------
RecursionError Traceback (most recent call last)
in
----> 1 recursion()
in recursion()
1 def recursion():
----> 2 return recursion()
... last 1 frames repeated, from the frame below ...
in recursion()
1 def recursion():
----> 2 return recursion()
RecursionError: maximum recursion depth exceeded
Ошибка отступа (IndentationError)
Эта ошибка похожа по духу на синтаксическую и является ее подвидом. Тем не менее она возникает только в случае проблем с отступами.
Пример:
for i in range(10):
print('Привет Мир!')
File "", line 2
print('Привет Мир!')
^
IndentationError: expected an indented block
Исключения
Даже если синтаксис в инструкции или само выражение верны, они все равно могут вызывать ошибки при исполнении. Исключения Python — это ошибки, обнаруживаемые при исполнении, но не являющиеся критическими. Скоро вы узнаете, как справляться с ними в программах Python. Объект исключения создается при вызове исключения Python. Если скрипт не обрабатывает исключение явно, программа будет остановлена принудительно.
Программы обычно не обрабатывают исключения, что приводит к подобным сообщениям об ошибке:
Ошибка типа (TypeError)
a = 2
b = 'PythonRu'
a + b
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
in
1 a = 2
2 b = 'PythonRu'
----> 3 a + b
TypeError: unsupported operand type(s) for +: 'int' and 'str'
Ошибка деления на ноль (ZeroDivisionError)
10 / 0
---------------------------------------------------------------------------
ZeroDivisionError Traceback (most recent call last)
in
----> 1 10 / 0
ZeroDivisionError: division by zero
Есть разные типы исключений в Python и их тип выводится в сообщении: вверху примеры TypeError и ZeroDivisionError. Обе строки в сообщениях об ошибке представляют собой имена встроенных исключений Python.
Оставшаяся часть строки с ошибкой предлагает подробности о причине ошибки на основе ее типа.
Теперь рассмотрим встроенные исключения Python.
Встроенные исключения
BaseException
+-- SystemExit
+-- KeyboardInterrupt
+-- GeneratorExit
+-- Exception
+-- StopIteration
+-- StopAsyncIteration
+-- ArithmeticError
| +-- FloatingPointError
| +-- OverflowError
| +-- ZeroDivisionError
+-- AssertionError
+-- AttributeError
+-- BufferError
+-- EOFError
+-- ImportError
| +-- ModuleNotFoundError
+-- LookupError
| +-- IndexError
| +-- KeyError
+-- MemoryError
+-- NameError
| +-- UnboundLocalError
+-- OSError
| +-- BlockingIOError
| +-- ChildProcessError
| +-- ConnectionError
| | +-- BrokenPipeError
| | +-- ConnectionAbortedError
| | +-- ConnectionRefusedError
| | +-- ConnectionResetError
| +-- FileExistsError
| +-- FileNotFoundError
| +-- InterruptedError
| +-- IsADirectoryError
| +-- NotADirectoryError
| +-- PermissionError
| +-- ProcessLookupError
| +-- TimeoutError
+-- ReferenceError
+-- RuntimeError
| +-- NotImplementedError
| +-- RecursionError
+-- SyntaxError
| +-- IndentationError
| +-- TabError
+-- SystemError
+-- TypeError
+-- ValueError
| +-- UnicodeError
| +-- UnicodeDecodeError
| +-- UnicodeEncodeError
| +-- UnicodeTranslateError
+-- Warning
+-- DeprecationWarning
+-- PendingDeprecationWarning
+-- RuntimeWarning
+-- SyntaxWarning
+-- UserWarning
+-- FutureWarning
+-- ImportWarning
+-- UnicodeWarning
+-- BytesWarning
+-- ResourceWarning
Прежде чем переходить к разбору встроенных исключений быстро вспомним 4 основных компонента обработки исключения, как показано на этой схеме.
Try: он запускает блок кода, в котором ожидается ошибка.Except: здесь определяется тип исключения, который ожидается в блокеtry(встроенный или созданный).Else: если исключений нет, тогда исполняется этот блок (его можно воспринимать как средство для запуска кода в том случае, если ожидается, что часть кода приведет к исключению).Finally: вне зависимости от того, будет ли исключение или нет, этот блок кода исполняется всегда.
В следующем разделе руководства больше узнаете об общих типах исключений и научитесь обрабатывать их с помощью инструмента обработки исключения.
Ошибка прерывания с клавиатуры (KeyboardInterrupt)
Исключение KeyboardInterrupt вызывается при попытке остановить программу с помощью сочетания Ctrl + C или Ctrl + Z в командной строке или ядре в Jupyter Notebook. Иногда это происходит неумышленно и подобная обработка поможет избежать подобных ситуаций.
В примере ниже если запустить ячейку и прервать ядро, программа вызовет исключение KeyboardInterrupt. Теперь обработаем исключение KeyboardInterrupt.
try:
inp = input()
print('Нажмите Ctrl+C и прервите Kernel:')
except KeyboardInterrupt:
print('Исключение KeyboardInterrupt')
else:
print('Исключений не произошло')
Исключение KeyboardInterrupt
Стандартные ошибки (StandardError)
Рассмотрим некоторые базовые ошибки в программировании.
Арифметические ошибки (ArithmeticError)
- Ошибка деления на ноль (Zero Division);
- Ошибка переполнения (OverFlow);
- Ошибка плавающей точки (Floating Point);
Все перечисленные выше исключения относятся к классу Arithmetic и вызываются при ошибках в арифметических операциях.
Деление на ноль (ZeroDivisionError)
Когда делитель (второй аргумент операции деления) или знаменатель равны нулю, тогда результатом будет ошибка деления на ноль.
try:
a = 100 / 0
print(a)
except ZeroDivisionError:
print("Исключение ZeroDivisionError." )
else:
print("Успех, нет ошибок!")
Исключение ZeroDivisionError.
Переполнение (OverflowError)
Ошибка переполнение вызывается, когда результат операции выходил за пределы диапазона. Она характерна для целых чисел вне диапазона.
try:
import math
print(math.exp(1000))
except OverflowError:
print("Исключение OverFlow.")
else:
print("Успех, нет ошибок!")
Исключение OverFlow.
Ошибка утверждения (AssertionError)
Когда инструкция утверждения не верна, вызывается ошибка утверждения.
Рассмотрим пример. Предположим, есть две переменные: a и b. Их нужно сравнить. Чтобы проверить, равны ли они, необходимо использовать ключевое слово assert, что приведет к вызову исключения Assertion в том случае, если выражение будет ложным.
try:
a = 100
b = "PythonRu"
assert a == b
except AssertionError:
print("Исключение AssertionError.")
else:
print("Успех, нет ошибок!")
Исключение AssertionError.
Ошибка атрибута (AttributeError)
При попытке сослаться на несуществующий атрибут программа вернет ошибку атрибута. В следующем примере можно увидеть, что у объекта класса Attributes нет атрибута с именем attribute.
class Attributes(obj):
a = 2
print(a)
try:
obj = Attributes()
print(obj.attribute)
except AttributeError:
print("Исключение AttributeError.")
2
Исключение AttributeError.
Ошибка импорта (ModuleNotFoundError)
Ошибка импорта вызывается при попытке импортировать несуществующий (или неспособный загрузиться) модуль в стандартном пути или даже при допущенной ошибке в имени.
import nibabel
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
in
----> 1 import nibabel
ModuleNotFoundError: No module named 'nibabel'
Ошибка поиска (LookupError)
LockupError выступает базовым классом для исключений, которые происходят, когда key или index используются для связывания или последовательность списка/словаря неверна или не существует.
Здесь есть два вида исключений:
- Ошибка индекса (
IndexError); - Ошибка ключа (
KeyError);
Ошибка ключа
Если ключа, к которому нужно получить доступ, не оказывается в словаре, вызывается исключение KeyError.
try:
a = {1:'a', 2:'b', 3:'c'}
print(a[4])
except LookupError:
print("Исключение KeyError.")
else:
print("Успех, нет ошибок!")
Исключение KeyError.
Ошибка индекса
Если пытаться получить доступ к индексу (последовательности) списка, которого не существует в этом списке или находится вне его диапазона, будет вызвана ошибка индекса (IndexError: list index out of range python).
try:
a = ['a', 'b', 'c']
print(a[4])
except LookupError:
print("Исключение IndexError, индекс списка вне диапазона.")
else:
print("Успех, нет ошибок!")
Исключение IndexError, индекс списка вне диапазона.
Ошибка памяти (MemoryError)
Как уже упоминалось, ошибка памяти вызывается, когда операции не хватает памяти для выполнения.
Ошибка имени (NameError)
Ошибка имени возникает, когда локальное или глобальное имя не находится.
В следующем примере переменная ans не определена. Результатом будет ошибка NameError.
try:
print(ans)
except NameError:
print("NameError: переменная 'ans' не определена")
else:
print("Успех, нет ошибок!")
NameError: переменная 'ans' не определена
Ошибка выполнения (Runtime Error)
Ошибка «NotImplementedError»
Ошибка выполнения служит базовым классом для ошибки NotImplemented. Абстрактные методы определенного пользователем класса вызывают это исключение, когда производные методы перезаписывают оригинальный.
class BaseClass(object):
"""Опередляем класс"""
def __init__(self):
super(BaseClass, self).__init__()
def do_something(self):
# функция ничего не делает
raise NotImplementedError(self.__class__.__name__ + '.do_something')
class SubClass(BaseClass):
"""Реализует функцию"""
def do_something(self):
# действительно что-то делает
print(self.__class__.__name__ + ' что-то делает!')
SubClass().do_something()
BaseClass().do_something()
SubClass что-то делает!
---------------------------------------------------------------------------
NotImplementedError Traceback (most recent call last)
in
14
15 SubClass().do_something()
---> 16 BaseClass().do_something()
in do_something(self)
5 def do_something(self):
6 # функция ничего не делает
----> 7 raise NotImplementedError(self.__class__.__name__ + '.do_something')
8
9 class SubClass(BaseClass):
NotImplementedError: BaseClass.do_something
Ошибка типа (TypeError)
Ошибка типа вызывается при попытке объединить два несовместимых операнда или объекта.
В примере ниже целое число пытаются добавить к строке, что приводит к ошибке типа.
try:
a = 5
b = "PythonRu"
c = a + b
except TypeError:
print('Исключение TypeError')
else:
print('Успех, нет ошибок!')
Исключение TypeError
Ошибка значения (ValueError)
Ошибка значения вызывается, когда встроенная операция или функция получают аргумент с корректным типом, но недопустимым значением.
В этом примере встроенная операция float получат аргумент, представляющий собой последовательность символов (значение), что является недопустимым значением для типа: число с плавающей точкой.
try:
print(float('PythonRu'))
except ValueError:
print('ValueError: не удалось преобразовать строку в float: 'PythonRu'')
else:
print('Успех, нет ошибок!')
ValueError: не удалось преобразовать строку в float: 'PythonRu'
Пользовательские исключения в Python
В Python есть много встроенных исключений для использования в программе. Но иногда нужно создавать собственные со своими сообщениями для конкретных целей.
Это можно сделать, создав новый класс, который будет наследовать из класса Exception в Python.
class UnAcceptedValueError(Exception):
def __init__(self, data):
self.data = data
def __str__(self):
return repr(self.data)
Total_Marks = int(input("Введите общее количество баллов: "))
try:
Num_of_Sections = int(input("Введите количество разделов: "))
if(Num_of_Sections < 1):
raise UnAcceptedValueError("Количество секций не может быть меньше 1")
except UnAcceptedValueError as e:
print("Полученная ошибка:", e.data)
Введите общее количество баллов: 10
Введите количество разделов: 0
Полученная ошибка: Количество секций не может быть меньше 1
В предыдущем примере если ввести что-либо меньше 1, будет вызвано исключение. Многие стандартные исключения имеют собственные исключения, которые вызываются при возникновении проблем в работе их функций.
Недостатки обработки исключений в Python
У использования исключений есть свои побочные эффекты, как, например, то, что программы с блоками try-except работают медленнее, а количество кода возрастает.
Дальше пример, где модуль Python timeit используется для проверки времени исполнения 2 разных инструкций. В stmt1 для обработки ZeroDivisionError используется try-except, а в stmt2 — if. Затем они выполняются 10000 раз с переменной a=0. Суть в том, чтобы показать разницу во времени исполнения инструкций. Так, stmt1 с обработкой исключений занимает больше времени чем stmt2, который просто проверяет значение и не делает ничего, если условие не выполнено.
Поэтому стоит ограничить использование обработки исключений в Python и применять его в редких случаях. Например, когда вы не уверены, что будет вводом: целое или число с плавающей точкой, или не уверены, существует ли файл, который нужно открыть.
import timeit
setup="a=0"
stmt1 = '''
try:
b=10/a
except ZeroDivisionError:
pass'''
stmt2 = '''
if a!=0:
b=10/a'''
print("time=",timeit.timeit(stmt1,setup,number=10000))
print("time=",timeit.timeit(stmt2,setup,number=10000))
time= 0.003897680000136461
time= 0.0002797570000439009
Выводы!
Как вы могли увидеть, обработка исключений помогает прервать типичный поток программы с помощью специального механизма, который делает код более отказоустойчивым.
Обработка исключений — один из основных факторов, который делает код готовым к развертыванию. Это простая концепция, построенная всего на 4 блоках: try выискивает исключения, а except их обрабатывает.
Очень важно поупражняться в их использовании, чтобы сделать свой код более отказоустойчивым.
Деление на ноль
- Определение
- Поведение программы
- Отслеживание деления на ноль
- Библиографический список
Определение
Деление на ноль — логическая программная ошибка, зачастую приводящая к ошибке времени выполнения, которая заключается в попытке деления любого числа на делитель, равный нулю.
Поведение программы
Возникновение ошибки времени выполнения зависит от многих факторов: как от языка и платформы разработки, так и от типа делимых чисел.
Согласно параграфу 5.6 стандарта языка Си++, если вторым операндом операторов «/» или «%» является 0, то в этом случае поведение не определено.
Попытка деления на целочисленный ноль на процессоре семейства x86 или x86_64 приводит к возникновению аппаратного исключения (по вектору 0); соответственно программа на Си или Си++, скомпилированная в машинный код, аварийно завершается при выполнении этого действия.
В то же время, если переменная, содержащая ноль, была вещественной — согласно стандарту IEEE 754, результатом будет вещественное число «плюс бесконечность» или «минус бесконечность» (согласно тому же стандарту, ноль также имеет знак) в случае ненулевого числителя, и «не-число» в случае неопределенности 0/0 (компилятор Microsoft Visual C++ возвращает специфичное для платформы x86 число «неопределенность»).
Следует учитывать, что сама переменная не обязательно должна содержать именно 0. Ноль может возникнуть при округлении, называемом исчезновением порядка (arithmetic underflow) — когда в результате операции получается число, значением меньше машинной точности. В таком случае результат считается равным 0.
Отслеживание деления на ноль
Ошибка деления ноль может отслеживаться некоторыми компиляторами (например, Microsoft Visual C++) и статическими анализаторами.
Особенно внимательно надо быть при делении на переменную-итератор цикла. Легко можно упустить из виду, что итератор в какой-то момент проходить через нулевое значение. Для этого в статическом анализаторе может быть использована специальная диагностика (например, V609 в анализаторе PVS-Studio).
Библиографический список
- Wikipedia. Division by zero.
- IEEE. IEEE Standard for Floating-Point Arithmetic (IEEE 754).
- MSDN. Know Your Bugs: Three Kinds of Programming Errors
- RSDN. Как перехватить исключение в случае деления на нуль.
- Перехват сообщений SIGSEGV (Segmentation Fault) и SIGFPE (Floating point exception).
Присылаем лучшие статьи раз в месяц
PostgreSQL, SQL, Блог компании OTUS. Онлайн-образование
Рекомендация: подборка платных и бесплатных курсов дизайна интерьера — https://katalog-kursov.ru/
В преддверии старта курса PostgreSQL подготовили небольшой полезный материал.
Большинство языков программирования предназначены для профессиональных разработчиков, знающих алгоритмы и структуру данных. Язык SQL немного отличается.
SQL используется аналитиками, специалистами по обработке данных, руководителями по программному продукту, проектировщиками и многими другими. Эти специалисты имеют доступ к базам данных, но у них не всегда есть интуиция и понимание, чтобы написать эффективные запросы.
Чтобы заставить сотрудников писать на SQL лучше, мы тщательно изучили отчеты, написанные не разработчиками, и код ревью, собрали распространенные ошибки и возможности по оптимизации в SQL.
Будьте внимательны во время деления целых чисел
В PostgreSQL деление целого числа на целое число в результате дает целое число. Не делайте так:
db=# (
SELECT tax / price AS tax_ratio
FROM sale
);
tax_ratio
----------
0Чтобы получить ожидаемый результат деления, вам нужно привести одно из значений к плавающему типу:
db=# (
SELECT tax / price::float AS tax_ratio
FROM sale
);
tax_ratio
----------
0.17Неспособность распознать эту ошибку может привести к крайне неточным результатам.
Защита от ошибок деления на ноль
Деление на ноль — известная ошибка:
db=# SELECT 1 / 0
ERROR: division by zeroДеление на ноль является логической ошибкой и ее нужно не просто «обойти», а исправить так, чтобы на первом месте у вас не было делителя, равного нулю. Однако бывают ситуации, когда возможен нулевой делитель. Один из простых способов защиты от ошибок деления на ноль — это присвоить всему выражению неопределенное значение, установив неопределенное значение делителю, если он равен нулю:
db=# SELECT 1 / NULLIF(0, 0);
?column?
----------
-Функция NULLIF возвращает неопределенное значение null, если первый аргумент равен второму. В этом случае, если знаменатель равен нулю.
При делении любого числа на NULL результатом будет NULL. Чтобы получить некоторое значение, вы можете свернуть все выражение с COALESCE и предоставить дефолтное значение:
db=# SELECT COALESCE(1 / NULLIF(0, 0), 1);
?column?
----------
1Функция COALESCE очень полезна. Она допускает любое количество аргументов и возвращает первое значение, которое не является неопределенным.
Знайте разницу между UNION и UNION ALL
Классический вопрос на собеседовании начального уровня для разработчиков и администраторов баз данных: «В чем разница между функциями UNION и UNION ALL?».
UNION ALL объединяет результаты одного или нескольких запросов. UNION делает то же самое, и к тому же исключает повторяющиеся строки. Не делайте так:
SELECT created_by_id FROM sale
UNION
SELECT created_by_id FROM past_sale
);
QUERY PLAN
-----------
Unique (cost=2654611.00..2723233.86 rows=13724572 width=4)
-> Sort (cost=2654611.00..2688922.43 rows=13724572 width=4)
Sort Key: sale.created_by_id
-> Append (cost=0.00..652261.30 rows=13724572 width=4)
-> Seq Scan on sale (cost=0.00..442374.57 rows=13570157 width=4)
-> Seq Scan on past_sale (cost=0.00..4018.15 rows=154415 width=4)В плане выполнения вы можете видеть, что после добавления двух запросов база данных отсортировала результаты и исключила повторяющиеся строки.
Если вам не нужно удалять повторяющиеся строки, лучше использовать функцию UNION ALL:
db=# (
SELECT created_by_id FROM sale
UNION ALL
SELECT created_by_id FROM past_sale
);
QUERY PLAN
-----------
Append (cost=0.00..515015.58 rows=13724572 width=4)
-> Seq Scan on sale (cost=0.00..442374.57 rows=13570157 width=4)
-> Seq Scan on past_sale (cost=0.00..4018.15 rows=154415 width=4)Выполняется намного проще. Результаты получены, сортировка не требуется.
Будьте внимательны при подсчете столбцов, допускающих неопределенное значение
При использовании агрегатных функций, таких как COUNT, важно понимать, как они обрабатывают неопределенные значения.
Например, возьмите следующую таблицу:
db=# pset null NULL
Null display is "NULL".
db=# WITH tb AS (
SELECT 1 AS id
UNION ALL
SELECT null AS id
)
SELECT *
FROM tb;
id
------
1
NULLСтолбец id содержит значение null. Посчитаем столбец id:
db=# WITH tb AS (
SELECT 1 AS id
UNION ALL
SELECT null AS id
)
SELECT COUNT(id)
FROM tb;
count
-------
1В таблице две строки, но функция COUNT возвращает 1. Это произошло, потому что функция COUNT игнорирует неопределенные значения.
Чтобы посчитать строки, используйте функцию COUNT(*):
db=# WITH tb AS (
SELECT 1 AS id
UNION ALL
SELECT null AS id
)
SELECT COUNT(*)
FROM tb;
count
-------
2Эта особенность также может быть полезна. Например, если поле с именем modified содержит неопределенное значение в том случае, если строка не была изменена, вы можете рассчитать процент измененных строк следующим образом:
db=# (
SELECT COUNT(modified) / COUNT(*)::float AS modified_pct
FROM sale
);
modified_pct
---------------
0.98Другие агрегатные функции, такие как SUM, будут игнорировать неопределенные значения. Для демонстрации применим функцию SUM к полю, содержащему только неопределенные значения:
db=# WITH tb AS (
SELECT null AS id
UNION ALL
SELECT null AS id
)
SELECT SUM(id::int)
FROM tb;
sum
-------
NULLЭто все документированные операции, так что будьте внимательны!
Обратите внимание на часовые пояса
Часовые пояса всегда являются источником путаницы и ошибок. PostgreSQL отлично справляется с часовыми поясами, но вам все равно придется обратить внимание на некоторые вещи.
Распространенной ошибкой, которую я вижу бесчисленное количество раз, является сокращение временных меток без уточнения часового пояса. Скажем, мы хотим узнать, сколько продаж было сделано каждый день:
SELECT created_at::date, COUNT(*)
FROM sale
GROUP BY 1Без точной настройки часового пояса вы можете получить разные результаты в зависимости от часового пояса, установленного приложением:
now
------------
2019-11-08
db=# SET TIME ZONE 'australia/perth';
SET
db=# SELECT now()::date;
now
------------
2019-11-09Если вы не уверены, с каким часовым поясом работаете, вы можете делать это неправильно.
При обращении к временной метке сначала приведите ее к нужному часовому поясу:
SELECT (timestamp at time zone 'asia/tel_aviv')::date, COUNT(*)
FROM sale
GROUP BY 1;
За установку часового пояса обычно отвечает приложение. Например, чтобы получить часовой пояс, используемый psql:
db=# SHOW timezone;
TimeZone
----------
Israel
db=# SELECT now();
now
-------------------------------
2019-11-09 11:41:45.233529+02А чтобы установить часовой пояс в PSQL:
db=# SET timezone TO 'UTC';
SET
db=# SELECT now();
now
-------------------------------
2019-11-09 09:41:55.904474+00Также важно помнить, что часовой пояс вашего сервера может отличаться от часового пояса вашего локального компьютера. Поэтому если вы выполняете запросы на локальном компьютере, они могут привести к разным результатам в готовом продукте. Чтобы избежать ошибок, всегда точно устанавливайте часовой пояс.
Избегайте преобразований в индексированных полях
Использование функций в индексированном поле может помешать базе данных использовать индекс в этом поле:
SELECT * FROM sale
WHERE created at time ZONE 'asia/tel_aviv' > '2019-10-01'
);
QUERY PLAN
----------
Seq Scan on sale (cost=0.00..510225.35 rows=4523386 width=276)
Filter: timezone('asia/tel_aviv', created) > '2019-10-01 00:00:00'::timestamp without time zoneПоле created индексируется, но поскольку мы преобразовали его с помощью часового пояса, индекс не использовался.
Один из способов использования индекса в этом случае — применить преобразование в правой части:
SELECT * FROM sale WHERE created > '2019-10-01' AT TIME ZONE 'asia/tel_aviv' );
QUERY PLAN
----------
Index Scan using sale_created_ix on sale (cost=0.43..4.51 rows=1 width=276)
Index Cond: (created > '2019-10-01 00:00:00'::timestamp with time zone)Другим примером использования дат является фильтрация определенного периода:
db=# (
SELECT * FROM sale WHERE created + INTERVAL '1 day' > '2019-10-01'
);
QUERY PLAN
----------
Seq Scan on sale (cost=0.00..510225.35 rows=4523386 width=276)
Filter: ((created + '1 day'::interval) > '2019-10-01 00:00:00+03'::timestamp with time zone)Как и до этого, интервальная функция в поле created препятствовала базе данных использовать индекс. Чтобы база данных использовала индекс, примените преобразование в правой части выражения вместо всего поля:
SELECT *
FROM sale
WHERE created > '2019-10-01'::date - INTERVAL '1 day'
);
QUERY PLAN
----------
Index Scan using sale_created_ix on sale (cost=0.43..4.51 rows=1 width=276)
Index Cond: (created > '2019-10-01 00:00:00'::timestamp without time zone)Заключение
Применение приведенных выше советов в повседневной жизни помогает нам поддерживать работоспособную базу данных с минимальными потерями. Мы обнаружили, что обучение разработчиков и не разработчиков тому, как лучше писать на SQL, может иметь большое значение. Если у вас есть какие-то советы по SQL, которые мы могли пропустить, дайте нам знать, и мы добавим их сюда!
Часть 1. Вобще-то уже все поделили до нас!
Часть 2. Истина где-то рядом
Говорят, можно поделить на ноль если определить результат деления на ноль. Просто нужно расширить алгебру. По странному стечению обстоятельств найти хоть какой-то, а лучше понятный и простой, пример такого расширения не удается. Чтобы исправить интернет нужна либо демонстрация одного из способов такого расширения, либо описание почему это не возможно.
Статья написана в продолжение тренда:
- Папа, а почему на ноль делить нельзя?
- Почему нельзя делить на ноль, даже если очень хочется?
Disclaimer
Цель данной статьи — объяснить «человеческим языком», как работают фундаментальные основы математики, структурировать знания и восстановить упущенные причинно-следственные связи между разделами математики. Все рассуждения являются философскими, в части суждений расходятся с общепринятыми (следовательно, не претендует на математическую строгость). Статья рассчитана на уровень читателя «сдал вышку много лет назад».
Понимание принципов арифметики, элементарной, общей и линейной алгебры, математического и нестандартного анализа, теории множеств, общей топологии, проективной и аффинной геометрии — желательно, но не обязательно.
В ходе экспериментов ни одна бесконечность не пострадала.
Пролог
Выход «за рамки» — это естественный процесс поиска новых знаний. Но не всякий поиск приносит новое знание и следовательно пользу.
1. Вобще-то уже все поделили до нас!
1.1 Аффинное расширение числовой прямой
Начнем с того, с чего начинают, наверное, все искатели приключений при делении на ноль. Вспомним график функции .
Слева и справа от нуля функция уходит в разные стороны «небытия». В самом нуле вообще “омут” и ничего не видно.
Вместо того, чтобы бросаться в «омут» с головой, посмотрим что туда втекает и что оттуда вытекает. Для этого воспользуемся пределом — основным инструментом математического анализа. Основная “фишка” в том, что предел позволяет идти к заданной точке так близко, как это возможно, но не “наступить на нее”. Такая себе “оградка” перед “омутом”.
Оригинал
Хорошо, «оградку» поставили. Уже не так страшно. У нас есть два пути к «омуту». Зайдем слева — крутой спуск, справа — крутой подъем. Сколько к “оградке” не иди, ближе она не становится. Пересечь нижнее и верхнее «небытие» никак не выходит. Возникают подозрения, может мы идем по кругу? Хотя нет, числа-то меняются, значит не по кругу. Пороемся в сундучке с инструментами математического анализа еще. Кроме пределов с «оградкой» в комплекте идет положительная и отрицательная бесконечности. Величины совершенно абстрактные (не являются числами), хорошо формализованы и готовы к употреблению! Это нам подходит. Дополним наше «бытие» (множество вещественных чисел) двумя бесконечностями со знаком.
Математическим языком:
Именно это расширение позволяет брать предел при аргументе стремящемся к бесконечности и получить бесконечность в качестве результата взятия предела.
Есть два раздела математики которые описывают одно и тоже используя разную терминологию.
С геометрической точки зрения выполнено аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел “сжата” так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины. Расширение аффинное, но это не значит что оно пришло из Греции, это значит что сохраняется относительное положение точек (в нашем случае чисел) на прямой. Отсюда и следует, что сохраняются отношения “больше” и ”меньше” как для чисел между собой, так и в сравнении с границами.
С точки зрения общей топологии выполнена двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком).
1.2 Проективное расширение числовой прямой
Прогуливаясь по графику , у нас есть только два пути к нулю (слева и справа). В конце каждого пути стоит небольшая «оградка». По странному стечению обстоятельств одна и та же «оградка» оказалась и на дне и на вершине «бытия». Если мы хотим чтобы пути сошлись, то за «оградкой» нам нужен телепорт из одного конца «бытия» в другой. Мы уже такие телепорты видали. Не проблема.
Попробуем состыковать обе границы «бытия» так, как это делали наши предки. Перейдем на одно измерение выше. Отобразим одномерную линию на двумерной плоскости.
После стыковки наличие двух знаковых бесконечностей теряет смысл. Вместо них можно ввести одну общую точку пересечения, беззнаковую бесконечность.
Эта стыковка очень похожа на линию перемены даты находящуюся (в основном), между часовыми поясами UTC+12 и UTC-12 в Тихом океане. Именно там находится телепорт из сегодня во вчера и из сегодня в завтра. У нас же телепорт из сверхмалых в сверхбольшие.
Математическим языком:
По факту это самостоятельное расширение, проведенное над исходным множеством вещественных чисел. Данное расширение не основывается на рассмотренном ранее аффинном расширении.
С геометрической точки зрения выполнено проективное расширение числовой прямой (есть информация на wolfram.com). То есть введена идеализированная точка которая соединяет оба конца вещественной прямой. Так как расширение не аффинное, сравнение вещественных чисел с бесконечностью не определено.
С точки зрения общей топологии выполнена одноточечная компактификация числовой прямой путем добавления идеализированной точки (бесконечности без знака).
Аналогичным расширением над полем комплексных чисел является широко известная в математических кругах Сфера Римана.
Хорошо, избавились от знака минус. Однако в нуле у нас разрыв второго рода и устранимой точкой разрыва его нельзя считать по определению. Нарушается требование «конечности» предела. Соответственно мы не можем судить о равенстве предела справа и слева.
Но так как приближение к бесконечности выполняется по одинаковым правилам, мы можем утверждать что пределы слева и справа совпадают. Соответственно мы можем принять наш разрыв за точку устранимого разрыва в бесконечности.
Математическим языком:
Посмотрим внимательнее, как мы оперируем бесконечно большими и малыми величинами. При операциях мы часто пренебрегаем малыми низшего порядка попросту отбрасывая их при записи результата.
Аналогичная ситуация при нахождении производных
Отбрасывая «мелочевку» мы теряем информацию! Это хорошо видно на примере взятия пределов. Рассмотрим две функции, которые стремятся к положительной бесконечности при стремлении аргумента к нулю справа.
Однако одинаковая запись результата взятия предела не свидетельствует о их равенстве. Данные бесконечности разного порядка и это подтверждается отсутствием конечного предела в отношении одной функции к другой.
В нестандартном анализе такие упрощения не допустимы. Поле вещественных чисел расширяется путем введения гиперреальных чисел. Бесконечно малые представлены в виде привычного значения — ноль, но в довесок хранится вся выкинутая “мелочевка”. Для бесконечно больших потенциальная бесконечность (две или одна — неважно), разбивается на множество актуальных бесконечностей. С одной стороны мы усложняем (теряем возможность поглощения/пренебрежения). С другой стороны мы приобретаем возможность сравнения бесконечно малых и бесконечно больших величин. А это значит что мы можем рассматривать бесконечности как числа.
Для функции
актуальные бесконечности слева и справа от нуля равны (по модулю, т.е. не учитывая знак), так как:
- с обеих сторон путь (количество элементов, которые нужно пройти) от нуля до бесконечности одинаков;
- алгоритм приближения (формула в виде дроби) одинаков;
- знак минус в алгоритме не влияет на скорость или ускорение приближения к бесконечности.
Стоит отметить что указанные критерии условны и не приведены к формальным определениям нестандартного анализа.
Для дальнейших рассуждений понятие актуальной бесконечности нам больше не потребуется. Мы возвращаемся в привычный мир где будем оперировать понятием бесконечность, подразумевая потенциальную бесконечность.
Хорошо, пределы совпадают. Теперь, похоже, все готово для устранения разрыва между ними.
В математической модели, использующей проективное расширение числовой прямой, деление на ноль определено.
Создается впечатление что наша задача решена. Однако не будем спешить, посмотрим к каким последствиям это привело. В дополнение к делению в системе определены следующие операции (напомним, что бесконечность беззнаковая).
Практически все они с дополнительными условиями, это настораживает. Но не будем спешить, лучше посмотрим на список неопределенных операций:
Посмотрим как будет вести себя дистрибутивный закон. Подставим в него определенные значения и выполним требуемые операции.
Как следствие, часть тождеств перестает вести себя так как мы привыкли. Однако, они не исчезли бесследно. Дистрибутивный закон работает только справа налево (т.е. в случае, когда правая часть равенства определена). Это один из ярких примеров негативных последствий. Другие же тождества сохранилась в более-менее устойчивой форме.
Подытожим:
- Изменилось привычное поведение тождеств. Чтобы ими оперировать, нужно не забывать про новые дополнительные условия.
- Искажено привычное поведение нуля. Мы привыкли рассуждать, если ноль раз взять что-либо, то будет ноль. Однако в данной алгебраической системе произведение нуля на бесконечность не определено. Соответственно алгебраическое выражение с переменными, в котором встречается например такая запись
, не может быть упрощено в одностороннем порядке.
- Исчезает возможность привычного сравнения. Сравнение на больше-меньше определено только на части пространства. Например, сравнение вещественных чисел с бесконечностью не определено.
- Полученная алгебраическая структура не поле в терминах общей алгебры. Нарушается дистрибутивный закон (показано выше). Так же не существует обратного элемента для бесконечности (произведение этого элемента и бесконечности должно дать единицу). Последние можно рассматривать как следствие неопределенности деления бесконечности на бесконечность. Но все же следует понимать что это грубое упрощение. Строгое определение обратного элемента не связано с операцией деления.
В сухом остатке. Старые подходы перестали работать. Сложность системы, в виде кучи “если”, “для всех, кроме” и т.п., возросла. У нас было только две неопределенности 1/0 и 0/0 (мы не рассматривали степенные операции), стало пять. Раскрытие одной неопределенности породило еще больше неопределенностей.
1.2 Колесо
На введении беззнаковой бесконечности все не остановилось. Для того чтобы выбраться из неопределенностей нужно второе дыхание.
Итак, у нас есть множество вещественных чисел и две неопределенности 1/0 и 0/0. Для устранения первой мы выполнили проективное расширение числовой прямой (то есть ввели беззнаковую бесконечность). Попробуем разобраться со второй неопределенностью вида 0/0. Сделаем аналогично. Дополним множество чисел новым элементом, представляющим вторую неопределенность.
Определение операции деления основано на умножении. Это нам не подходит. Отвяжем операции друг от друга, но сохраним привычное поведение для вещественных чисел. Определим унарную операцию деления, обозначаемую знаком «/».
Доопределим операции.
Данная структура называется «Колесом» (Wheel). Термин был взят из-за схожести с топологической картинкой проективного расширения числовой прямой и точки 0/0.
Вроде все неплохо выглядит, но дьявол кроется в деталях:
Чтобы устаканить все особенности, дополнительно к расширению множества элементов прилагается бонус в виде не одного, а двух тождеств, описывающих дистрибутивный закон.
Математическим языком:
С точки зрения общей алгебры мы оперировали полем. А в поле, как известно, определены всего две операции (сложение и умножение). Понятие деления выводится через обратные, а если еще глубже, то единичные элементы. Внесенные изменения превращают нашу алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента).
В трудах первооткрывателей не всегда используются символы ∞ и ⊥. Вместо этого можно встретить запись в виде /0 и 0/0.
Мир уже не так прекрасен, не правда ли? Все же не стоит спешить. Проверим, справятся ли новые тождества дистрибутивного закона с нашим расширенным множеством .
На этот раз результат намного лучше.
Подытожим:
- Все операции хорошо определены и нет возможности «вывалиться за борт».
- Элементарная алгебра является частным случаем колеса. Если мы отбросим надстройки ∞ и ⊥ (то есть снова сможем утверждать что
и
), то все формулы выродятся в привычные.
- По ощущениям все что было “не определено” (Undefined) при проективном расширении было обозначено символом
. Данный объект так же поглощает все с чем столкнется как и “не определено”. Все щели, где появились неопределенности при проективном расширении, были заткнуты данным объектом.
В сухом остатке. Алгебра работает отлично. Однако за основу было взято понятие «не определено» которое стали считать чем-то существующим и оперировать им. Однажды кто-нибудь скажет, что все плохо и нужно разбить данное «не определено» еще на несколько “не определено», но помельче. Общая алгебра скажет: “Без проблем, Бро!».
Примерно так постулированы дополнительные (j и k) мнимые единицы в кватернионах.
Стоит отметить, существуют и другие алгебраические системы с делением. Например, «луга» (common meadows). Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а так же отказом от бинарного деления.
Возможность «передвигать неизвестные» для математики норма. Но все эти обертки не дают ответа на главный вопрос, что же там внутри?
Полезная литература
- Setzer, Anton (Drafts): Wheels, 1997 (pdf)
- Carlström, Jesper: Wheels — on division by zero, 2001 (pdf)
- P. J. Potts: Exact Real Arithmetic using Möbius Transformations, 1998 (pdf)
- Jan A. Bergstra & Alban Ponse: Division by Zero in Common Meadows (pdf)
- A.Edalat and P. J. Potts. A new representation for exact real numbers, 2000
- http://en.wikipedia.org/wiki/Undefined_(mathematics)
- http://en.wikipedia.org/wiki/Wheel_theory
- Форум dxdy — Деление на ноль (2)
- Форум dxdy — Деление на ноль возможно (12)
Improve Article
Save Article
Improve Article
Save Article
We use Exception Handling to overcome exceptions occurred in execution of a program in a systematic manner.
Dividing a number by Zero is a mathematical error (not defined) and we can use exception handling to gracefully overcome such operations. If you write a code without using exception handling then the output of division by zero will be shown as infinity which cannot be further processed.
Consider the code given below, the Division function returns the result of numerator divided by denominator which is stored in the variable result in the main and then displayed. This Division function does not have any rumination for denominator being zero.
#include <iostream>
using namespace std;
float Division(float num, float den)
{
return (num / den);
}
int main()
{
float numerator = 12.5;
float denominator = 0;
float result;
result = Division(numerator, denominator);
cout << "The quotient of 12.5/0 is "
<< result << endl;
}
Output:
The quotient of 12.5/0 is inf
We can handle this exception in a number of different ways, some of which are listed below
- 1) Using the runtime_error class
The runtime_error class is a derived class of Standard Library class exception, defined in exception header file for representing runtime errors.
Now we consider the exact same code but included with handling the division by zero possibility. Here, we have the try block inside main that calls the Division function. The Division function checks if the denominator passed is equal to zero if no it returns the quotient, if yes it throws a runtime_error exception. This Exception is caught by the catch block which prints the message “Exception occurred” and then calls the what function with runtime_error object e. The what() function {used in the code given below} is a virtual function of the class Standard exception defined in stdexcept header file, it is used to identify the exception. This prints the message “Math error: Attempted to divide by Zero”, after which the program resumes the ordinary sequence of instructions.#include <iostream>#include <stdexcept> // To use runtime_errorusingnamespacestd;floatDivision(floatnum,floatden){if(den == 0) {throwruntime_error("Math error: Attempted to divide by Zeron");}return(num / den);}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{result = Division(numerator, denominator);cout <<"The quotient is "<< result << endl;}catch(runtime_error& e) {cout <<"Exception occurred"<< endl<< e.what();}}Output:
Exception occurred Math error: Attempted to divide by Zero
- 2) Using User defined exception handling
Here we define a class Exception that publicly inherits from runtime_error class. Inside the class Exception, we define only a constructor that will display the message “Math error: Attempted to divide by Zero” when called using the class object. We define the Division function that calls the constructor of class Exception when denominator is zero otherwise returns the quotient. Inside of main we give some values to numerator and denominator, 12.5 and 0 respectively. Then we come to the try block that calls the Division function which will either return the quotient or throw an exception. The catch block catches the exception of type Exception, displays the message “Exception occurred” and then calls the what function. After the exception is handled the program resumes.
#include <iostream>#include <stdexcept>usingnamespacestd;classException :publicruntime_error {public:Exception(): runtime_error("Math error: Attempted to divide by Zeron"){}};floatDivision(floatnum,floatden){if(den == 0)throwException();return(num / den);}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{result = Division(numerator, denominator);cout <<"The quotient is "<< result << endl;}catch(Exception& e) {cout <<"Exception occurred"<< endl<< e.what();}}Output:
Exception occurred Math error: Attempted to divide by Zero
- 3) Using Stack Unwinding
In stack unwinding we have the main inside which the try block calls the Division function which in turn calls the CheckDenominator function. The CheckDenominator function checks if denominator is zero, if true throws an exception otherwise returns the value of denominator. The Division function calculates the value of quotient {if non-zero value of denominator was passed} and returns the same to the main. The catch block catches any exception thrown and displays the message “Exception occurred” and calls the what function which prints “Math error: Attempted to divide by zero”. After this the program resumes.
#include <iostream>#include <stdexcept>usingnamespacestd;floatCheckDenominator(floatden){if(den == 0) {throwruntime_error("Math error: Attempted to divide by zeron");}elsereturnden;}floatDivision(floatnum,floatden){return(num / CheckDenominator(den));}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{result = Division(numerator, denominator);cout <<"The quotient is "<< result << endl;}catch(runtime_error& e) {cout <<"Exception occurred"<< endl<< e.what();}}Output:
Exception occurred Math error: Attempted to divide by zero
- 4) Using try and catch(…)
In this code the try block calls the CheckDenominator function. In CheckDenominator function we check if denominator is zero, if true throw an exception by passing a string “Error”. This string is caught by the catch block and therefore prints the message “Exception occurred”. The catch block here is capable of catching exception of any type.
#include <iostream>#include <stdexcept>usingnamespacestd;floatCheckDenominator(floatden){if(den == 0)throw"Error";elsereturnden;}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{if(CheckDenominator(denominator)) {result = (numerator / denominator);cout <<"The quotient is "<< result << endl;}}catch(...) {cout <<"Exception occurred"<< endl;}}Output:
Exception occurred
Improve Article
Save Article
Improve Article
Save Article
We use Exception Handling to overcome exceptions occurred in execution of a program in a systematic manner.
Dividing a number by Zero is a mathematical error (not defined) and we can use exception handling to gracefully overcome such operations. If you write a code without using exception handling then the output of division by zero will be shown as infinity which cannot be further processed.
Consider the code given below, the Division function returns the result of numerator divided by denominator which is stored in the variable result in the main and then displayed. This Division function does not have any rumination for denominator being zero.
#include <iostream>
using namespace std;
float Division(float num, float den)
{
return (num / den);
}
int main()
{
float numerator = 12.5;
float denominator = 0;
float result;
result = Division(numerator, denominator);
cout << "The quotient of 12.5/0 is "
<< result << endl;
}
Output:
The quotient of 12.5/0 is inf
We can handle this exception in a number of different ways, some of which are listed below
- 1) Using the runtime_error class
The runtime_error class is a derived class of Standard Library class exception, defined in exception header file for representing runtime errors.
Now we consider the exact same code but included with handling the division by zero possibility. Here, we have the try block inside main that calls the Division function. The Division function checks if the denominator passed is equal to zero if no it returns the quotient, if yes it throws a runtime_error exception. This Exception is caught by the catch block which prints the message “Exception occurred” and then calls the what function with runtime_error object e. The what() function {used in the code given below} is a virtual function of the class Standard exception defined in stdexcept header file, it is used to identify the exception. This prints the message “Math error: Attempted to divide by Zero”, after which the program resumes the ordinary sequence of instructions.#include <iostream>#include <stdexcept> // To use runtime_errorusingnamespacestd;floatDivision(floatnum,floatden){if(den == 0) {throwruntime_error("Math error: Attempted to divide by Zeron");}return(num / den);}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{result = Division(numerator, denominator);cout <<"The quotient is "<< result << endl;}catch(runtime_error& e) {cout <<"Exception occurred"<< endl<< e.what();}}Output:
Exception occurred Math error: Attempted to divide by Zero
- 2) Using User defined exception handling
Here we define a class Exception that publicly inherits from runtime_error class. Inside the class Exception, we define only a constructor that will display the message “Math error: Attempted to divide by Zero” when called using the class object. We define the Division function that calls the constructor of class Exception when denominator is zero otherwise returns the quotient. Inside of main we give some values to numerator and denominator, 12.5 and 0 respectively. Then we come to the try block that calls the Division function which will either return the quotient or throw an exception. The catch block catches the exception of type Exception, displays the message “Exception occurred” and then calls the what function. After the exception is handled the program resumes.
#include <iostream>#include <stdexcept>usingnamespacestd;classException :publicruntime_error {public:Exception(): runtime_error("Math error: Attempted to divide by Zeron"){}};floatDivision(floatnum,floatden){if(den == 0)throwException();return(num / den);}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{result = Division(numerator, denominator);cout <<"The quotient is "<< result << endl;}catch(Exception& e) {cout <<"Exception occurred"<< endl<< e.what();}}Output:
Exception occurred Math error: Attempted to divide by Zero
- 3) Using Stack Unwinding
In stack unwinding we have the main inside which the try block calls the Division function which in turn calls the CheckDenominator function. The CheckDenominator function checks if denominator is zero, if true throws an exception otherwise returns the value of denominator. The Division function calculates the value of quotient {if non-zero value of denominator was passed} and returns the same to the main. The catch block catches any exception thrown and displays the message “Exception occurred” and calls the what function which prints “Math error: Attempted to divide by zero”. After this the program resumes.
#include <iostream>#include <stdexcept>usingnamespacestd;floatCheckDenominator(floatden){if(den == 0) {throwruntime_error("Math error: Attempted to divide by zeron");}elsereturnden;}floatDivision(floatnum,floatden){return(num / CheckDenominator(den));}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{result = Division(numerator, denominator);cout <<"The quotient is "<< result << endl;}catch(runtime_error& e) {cout <<"Exception occurred"<< endl<< e.what();}}Output:
Exception occurred Math error: Attempted to divide by zero
- 4) Using try and catch(…)
In this code the try block calls the CheckDenominator function. In CheckDenominator function we check if denominator is zero, if true throw an exception by passing a string “Error”. This string is caught by the catch block and therefore prints the message “Exception occurred”. The catch block here is capable of catching exception of any type.
#include <iostream>#include <stdexcept>usingnamespacestd;floatCheckDenominator(floatden){if(den == 0)throw"Error";elsereturnden;}intmain(){floatnumerator, denominator, result;numerator = 12.5;denominator = 0;try{if(CheckDenominator(denominator)) {result = (numerator / denominator);cout <<"The quotient is "<< result << endl;}}catch(...) {cout <<"Exception occurred"<< endl;}}Output:
Exception occurred
По-моему, надо честно признаться, что математики просто ещё не придумали, что будет, если делить на ноль. С тем же успехом можно было когда-то сказать, что нельзя вычислять квадратные корни из отрицательных чисел: ну как же ВЕДЬ НЕТ такого числа, которое при умножении самого на себя даёт отрицательное число!
Ответить
-
Почему не придумали, придумали — если устремить к нулю делитель, то будет бесконечность. И почему нельзя квадратный корень из отрицательного числа вычислять — возьмите комплексную плоскость и будет вам корень. Над R же не существует числа, которое при умножении на самоее себя давало бы отрицательное значение.
Ответить
-
а что такое квадратный корень ?
Ответить
-
Квадратный корень определяется как обратная операцию к умножению.
Q является квадратным корнем из R, если Q * Q = R
На множестве целых чисел эта операция определена только для некоторых положительных чисел, например, для 1, 4, 9, 16, 25. На множестве вещественных чисел эта операция определена для любого положительного числа. На комплексной плоскости квадратный корень определен всюду.
Ответить
-
-
-
На ноль формально делить нельзя, но можно неограниченно стремить знаменатель к нулю, а дробь будет стремится к бесконечности. в мат. анализе можно делить на ноль и полить бесконечность, так и пишут. хотя бесконечность это не число, а условность, тем не менее при делении любого конечного числа на ноль можно сказать что дробь стремится к бесконечности.
Я вам скажу что понятие НЕЛЬЗЯ в математике нет. Просто раньше невозможно было сказать, что будет если взять корень (четной степени) из отрицательного числа. Т.е. математика того времени не могла это описать. Результат лежит вне множества действительных чисел. И если ввести новое множества — множество мнимых (комплексных) чисел, то это явление описывается легко : i^2 = -1Ответить
-
Libach
Jabberwok
06.05.2006
11:44
Ответить
В математике понятие «нельзя» равносильно понятию «не определено».
В матане нельзя делить на нуль, как и в арифметике. Последовательность n/0, n — натуральное, не определена, поэтому никуда она не стремится.
В математике, основанной на аксиомах, использующихся сейчас, деление на нуль определять никогда не будут.
Ответить
-
taras
Jabberwok
11.10.2017
16:18
Ответить
НЕЛЬЗЯ поливать бесконечность.
Ответить
-
-
!ё! написал: «Но не забывайте, что как только знаменатель в этом стремлении, хотя бы теоретически в пределе достигнет 0 …»
Речь идет о пределе последовательности. С ростом номера знаменатель становится все ближе и ближе к нулю, но нулем он никогда не будет.
Вам, !ё!, очень не мешало бы ознакомиться хотя бы с азами матанализа (теория пределов).
Ответить
-
-
!ё! написал:
<
Теория пределов, хотя и основана на бесконечном стремлении чего-то к чему-то, преследует практические цели. Поэтому, хотя абстрактно-математически предел недостижим, теоретически он предназначен для определения каких-либо параметров именно в предельной точке. Разве не так?
>
Конечно не так!<
Разумеется речь идёт о достижении точки с какой-то точностью, достаточной для того, чтобы хотя бы практически считать её достигнутой. Не правда ли?
>
Нет, не правда.Всё, что вы тут и раньше понаписали, к математике не имеет никого отношения.
Есть люди, которые способны понять математику, а есть такие, которые к этому не способны из-за неразвитости абстрактного мышления.
Например, некто понимает, что 7 — 2 равно пяти:
было семь яблок, потом два отобрали, осталось пять.Но 2-7 он уже понять не может, он возмущается : как можно забрать у меня семь яблок, если их всего два.
Или такой пример. Он понимает, что 6/3 равно два: мама принесла шесть яблок, у нее трое сыновей, она их поровну поделила, и каждому сыночку досталось по два яблока.
Но 6/0.5 он уже понять не в состоянии, он возмущается: как можно разделить шесть яблок на половину человека? Не бывает половины человека.
Похожая ситуация с нулем. В математике результат деления на ноль НЕ определен. Далеко не все способны понять, что в точности это означает, хотя всё это очень просто.
Ответить
-
-
-
-
-
эээээ. никто ведь не говорит о вычислении корня из минус единицы. Просто ввели новое понятие. Расширили множество чисел. Разрешили проблему введением новых понятий. Это кстати относится к теореме Геделя. Здесь проблема в другом.
Ответить
-
корень из минус-единицы ввели потому, что тут есть единственность и экономия — введением всего лишь ОДНОГО понянтия можно описать получение корней из всех отрицательных чисел. Выход — надо ввести число ‘зю’.
i — число, умножение которого на само себя дает -1.
зю — число умножение которого на ноль дает единицу5/0 = х
х*0 = 5
x*0*зю = 5*зю
x = 5*зюТеперь результат математической операции, например, ‘деления пяти на ноль’ вполне определен — это ‘пять зю’ ;-)) Наверное за этим должен последовать крутой прорыв в науке, включая перемещение во времени, сверхсветовые скорости, доказательства существования жизни после смерти, контакт с инопланетянами итп…
Ответить
-
«i — число, умножение которого на само себя дает -1.
зю — число умножение которого на ноль дает единицу5/0 = х
х*0 = 5
x*0*зю = 5*зю
x = 5*зю» И что дальше? Мнимые числа можно умножать, делить, вычитать, складывать. А зю? Чему равно например, зю в квадрате? А зю-зю чему равно? 0*зю? А по каким правилам умножать 0*зю? И таких вопросов будет больше, чем математиков.Ответить
-
-
Как раз давно придумали.
Ответить
Можно привести еще более простой пример. Допустим, на ноль делить можно. Оказывается, что такое допущение позволяет доказать любое утверждение. Начнем с тождества:
0*2=0*3
Сократим на ноль. Получим:
2=3
То есть, допущение возможности деления на ноль приводит к выводу, что любые два числа равны между собой. Поскольку любому утверждению можно сопоставить некий числовой код (ну, хотя бы последовательность кодов символов, которыми записано это утверждение), то из возможности деления на ноль, оказывается следует тождественность любых двух утверждений.
Подводя итог: если можно делить на ноль, то Луна сделана из швейцарского сыра.
Ответить
-
Injener
APXIMHD
20.05.2006
14:11
Ответить
НЕПРАВИЛЬНО! Сократим на ноль — это значит поделим на ноль левую и правую часть уравнения. Получим неопредленность типа ноль/ноль.
На самом деле есть неопределенности в математике. Такие например как отношение двух бесконечностей.
А делением на ноль уже никого не испугаешь и там все справедливо.Ответить
-
НУ УЖ НЕТ! Здесь речь идет о доказательстве от противного!
И если мы предположили, что на нуль делить МОЖНО, то ни о каких неопределенностях типа нуль на нуль уже речи не идет!Ответить
-
Неопределённости ТИПА 0/0. бесконечно малое на бескончно малое. тут вопрос кто быстрее стремится к нулю.
Ответить
-
taras
Melethron
11.10.2017
16:27
Ответить
Не будет вопроса о стремлении. Он существует только пока делить нельзя.
Ответить
-
-
-
Неопределённость получится только в случае, если на ноль делить нельзя. А если можно, то ни какой неопределённости не возникнет, так как всякое допустимое деление однозначно.
Ответить
-
А по-моему,все правильно объяснено для школьников и добавлено,что в институте на ноль делить все же придется:))
Ответить
-
Ничего правильного тут нет. А самая главная неправильность в том, что в школе нам рассказывают всякую чушь, которая на самом деле не верна. Как то: невозможность деления на ноль, рассказы про строение атома(Боровская модель), то что человек произошел от обезьяны и т.д. (по поводу обезьяны я точно сказать не могу, так как я физик, а не биолог). Неснясным остается следующее — зачем заведомо неверную информацию вводить в школьную программу, может быть проще сразу рассказывать как оно есть на самом деле?
Ответить
-
Думается, что это как раз тот случай, когда истина где-то посередине. Данная статья объясняет всё на уровне, достаточном для понимания среднего подростка 12-14 лет. А что касается более научного объяснения, то надо иметь в виду, что операции над математическим объектами вводятся с целью обеспечить адекватность математических моделей действительности. С этой точки зрения деление на нуль — операция корректная, но для её описания необходимо оперировать терминами теории функций пространственного комплексного переменного… По-моему, даже на матфаках университетов немногие представляют себе, что это такое. Явно не детский вопрос!
Ответить
-
Кажется, по поводу упомянутой ТФПКП (Если имеется в виду теория Елисеева) все не утихают споры — считать ли ее корректной.
Ответить
-
Я думаю,что если возникают такие вопросы такие,как почему нельзя делить на нуль или откуда произошел человек надо отвечать детям с точки зрения науки ,даже если это очень сложно в понимании.
Ответить
-
Нет. Операция как раз некорректная.
Ответить
-
-
Orange03
Injener
13.07.2013
01:49
Ответить
Я могу ответить на вопрос, почему детям сразу не рассказывают все как есть, но это уже немного другая тема.
Просто говоря, дебилами проще управлять. Политикам выгодно, что бы народ их слушался, что бы народ был глуп. Вот ни кто и не заморачивается над тем, что бы создать реально хорошую и продвинутую программу. Проще же сделать так, оставить все как есть.Ответить
-
В «США» да. Но дебил на АЭС, или дебил, пытающийся сварить сталь, продуть её на АКОС и разлить на МНЛЗ, как раз не управляем вообще. Более того, такой дебил ОПАСЕН.
Ответить
-
-
Чушь несёшь как раз ты.
Ответить
-
-
Нет. В институте на ноль тоже не делят. Вычисление пределов — это всё таки не деление.
Ответить
А вот учительница в первом классе ашдодской школы учила моего сына:
3 : 0 = 0. И никто из родителей этого не эаметил. Когда я пыталась обратить внимание других родителей на этот факт, мне говорили: «Ну и зануда ты, просто придираешься к учительнице». Интересно, как эта учительница преподает в нашей школе уже 12 лет?
Ответить
-
aleks
lior-kauf
17.07.2006
18:16
Ответить
А что такое «ноль» и что такое число. Это наличие и отсутствие. Как наличие делить на отсуствие. Наличие проявляется на фоне отсутствия. Или вернее даже отсуствие проявляется на фоне наличия. Тут уже нейрофизиология и просхождение разума, Как человек осознал. Так что вопрос только кажется детским, а наукой не проясненный до конца. Возбуждение нейрона -1 , отсуствие возбуждения 0. Отсуствие не количественное понятие, это отсуствие колличества. А наличие колличественное понятие. В одном наличии может быть несколько наличий.
Ноль и число совершенно разные понятия. Ноль не число-проще говоря. Число делить на не число нельзя .Ответить
-
Само выражение «не имеет смысла» уже абсурдно! Смысл имеет все! Фраза «уравнение не имеет решения» еще более нелепа. Любое уравнение имеет решение, его просто надо найти и доказать, даже если оно пустое!
«Математики признают полноценными только два из них — сложение и умножение.»
НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания).«0 * x = 5» и далее «То есть наша задача не имеет решения.»
Решение есть! И оно пустое. То, что нам может не нравиться подобные результаты никого не е…(волнует), оно все равно существует!«Да, такое бывает, не у всякой задачи есть решение»
Вообще атас! Думаю комментарии излишне. Вот они — плоды того, чему учат в школе. Любая задача имеет решение!По поводу «0 * x = 0» вообще смех, да и только. Решение не то, что существует, а вообще предоставляет полную свободу выбора. Бери любое число, оно и будет тебе решением. Ну, нет же! У нас ответ: «Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них.» Бред сивой кобылы!
И дальше:
«А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла.» Как же не имеет никакого смысла, когда имеет, и еще какой! Например, если Мы будем постоянно бегать с пустым ведром от колодца к бочке, то бегай хоть 100, хоть 1000 раз — воды Мы не принесем. Уравнение это четко показывает, и имеет очень даже хороший смысл…Теперь давайте разбираться по поводу деления на ноль («нуль» не люблю — устарело).
Проблема в том, как уже ранее было замечено, что существует некая путаница в понятиях и их значениях. Стоит также отметить, что Мы частично признаем (не признаем) полярные стороны. Другими словами «бесконечность» числом считать не принято, а вот ноль (как было замечено «ничто») числом мы считаем. А если так, то чего же мы тогда хотим? Связать два понятия находящихся «в двух разных весовых категориях»? Ноль и бесконечность должны стоять по одну сторону баррикады, сейчас же они по разные.К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». Все эти числа принадлежат одному множеству и, следовательно, сопоставимы. Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо.
Ответить
-
Я имел в виду не «делить» а «разделить». Если наличие -это конечное множество. А «ноль» это отсутствие. «Ноль» — отсутствие наличия. Допустим есть множество. Если его необходимо разделить на кучки. Не может быть 0,4 кучки. Минимум может быть две кучки и остаток. Я опустился на один уровень ниже. С психического уровня на биологический. Я предположил какая математика в биологии может быть. В биологии с сенсорных нейронов приходит сигнал, или отсутствие сигнала. С ними живое и производит математические операции. Есть конечное множество сигналов от рецепторов, допустим глаз. И живое, его нервная система классифицирует сигналы, сравнивает и раскладывает на кучки по какому то признаку. Что не поддалось классификации-то в остаток. В живом действует особая математика ,еще не описанная нигде. Между математикой количества и математикой событий межит огромный пласт неиследованой математики систем или математики живого. Обычной математикой невозможно обработать поступающие сигналы от рецепторов.
Ответить
-
Прочитал статью — огромное спасибо!
Сегодня обязательно детям расскажу почему нельзя делить на 0студент МГУ
Ответить
-
Есть у тебя лента, а я у тебя прошу кусочек ленты. Ты можешь мне отрезать и 0,4 своей ленты, и даже 0,0055.
Ответить
-
-
nickhunter
dvaman
22.02.2007
12:04
Ответить
Критика, в целом, довольно спорная (в отличии от статьи, которая спорна с точки зрения чистой математики, но, на мой взгляд, хороша для образовательных целей).
Но больше всего смущает Ваш аргумент по поводу программирования.
Цитата:
«К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». Все эти числа принадлежат одному множеству и, следовательно, сопоставимы. Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо.»В реальности:
В программировании не определено, не принадлежат, не получим. Более того, в программировании, вообще говоря, существует понятие типа (и расположено оно на пару уровней абстракции выше, чем понятия об архитектуре ЭВМ), только осознав которое можно говорить о каких-либо операциях с данными вообще!Ответить
-
«…Математики признают полноценными только два из них — сложение и умножение.» НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать,…»
— неправда Ваша. Грош-цена такому компутеру.
Компутер — он ить не только «складывает» — он еще и СДВИГАЕТ(коия операция как раз и эквивалентна операции умножения или деления — смотря куда двигать ;), а помимо того — ЛЮБОЙ компутер еще ОБЯЗАТЕЛЬНО выполняет побитовые операции — ИНВЕРСИИ, И, ИЛИ, искл.ИЛИ. И вообще — смотря про какой компутер говорить. Есть и таке — которые не только умножают — но и делят аппаратно… и даже не одно число — а матрицы…
;))«…Ноль и бесконечность должны стоять по одну сторону баррикады, сейчас же они по разные. К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». … Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. …»
— ?!!!
марку, марку ЭТОГО чуднОго компутера — в студию!!
На моей памяти — а работал я с добрым десятком самых разных компутеров и процессоров — от БЭСМ-4 до PowerPC880. И — ВЕЗДЕ(!) — при обнаружении деления на «0» — процесоры выдают специальное ПРЕРЫВАНИЕ —
по которому отрабатывается либо утилита обработки исключительной ситуации(если такая предусмотрена программистом) — либо вооще процесс вычисления ОСТАНАВЛИВАЕТСЯ(поскольку по-умолчанию вектор этого прерывания — нулевой). И только в специализированных(!) процессорах обработки сигналов(типа TMS320Cxxx) есть нечто подобное — и то не для деления на нуль — а для переполнения. То есть если к Вашему «max_value-1» прибавить 3, то получится не «-2», а просто «max_value» — и то там этот режим ОПЦИОНАЛЕН — то есть при желании его можно ВКЛЮЧИТЬ.— а деление на нуль — дело сурьезное — с ним шутки плохи.
интеррупт — и весь сказ!Ответить
-
Респект, до этого сообщения думал что комменты пишут несгибаемые и..ы
Ответить
-
Ну, ещё надо добавить, что обычный интеловский процессор может обрабатывать числа с плавающей точкой в двух режимах: в одном, действительно, при делении на ноль возникает прерывание, а в другом — прерывания нет, но получается результат «не определено». Соотвественно, формат для чисел с плавающей точкой придуман такой, что в нём можно задать не только обычные числа, но и специальные константы «не определено», «плюс бесконечность», «минус бесконечность» и ещё несколько вариантов, все не помню. Очень удобная, кстати, штука, но доступна только на ассемблере.
Ответить
-
Во-первых inf, а не nan. А во-вторых этот режим отлично доступен на c++. А вот как получить при делении с плавающей точкой прерывание — это для меня загадка.
Ответить
-
-
«То есть если к Вашему «max_value-1» прибавить 3, то получится не «-2», а просто «max_value» — и то там этот режим ОПЦИОНАЛЕН — то есть при желании его можно ВКЛЮЧИТЬ.» MAX_INT — обычное значение типа INTEGER НА ЛЮБОМ компьютере и при инкементе, например, 32 767 двухбайтной версии INTEGER MAX_INT получится гарантированно. А переполнение происходит при СЛЕДУЮЩЕМ инкременте. А если прибавить к MAX_INT сразу 3, то получите -32 766 (в двухбайтной версии). И опционально только то, будет ли ИДЕНТИФИКАТОР MAX_INT известен компилятору. И то на уровне языка, а не компьютера. Соответственно на БЭСМ его ещё не было, потому что тогда профессиональные программисты то уж точно знали, чему эта константа равна, так как переносимостью по-настоящему озаботились позже, а остальным это было не нужно. Но если сейчас портировать современный диалект паскаля на БЭСМ, то MAX_INT будет и там. А вот на сигнальных камнях MAX_INT водится только ради того, чтоб сообщение об ошибке unknown identificator не выскочило неожиданно, если как какой нибудь предназначенный для таких камней код сначала опробован на компьютере и только потом «скормить» кроскомпилятору.
#include
int main()
{
double x=5.0;
double y=0.0;
double z=x/y;
std::cout<<z;
int main()
{
int x=5.0;
int y=0.0;
int z=x/y;
std::cout<<z;
return 0;
}
результат — аварийное завершение программы. Комп один и тот же. Процессор Intel(R) Pentium(R) CPU J2900 @ 2.41GHz.Ответить
-
-
Я понимаю, что я злостный некропостер, но не могу удержаться.
1) © Само выражение «не имеет смысла» уже абсурдно! Смысл имеет все! ©
Сытый конному не пеший.2) © Любое уравнение имеет решение, его просто надо найти и доказать, даже если оно пустое! ©
Вы путаете понятия. «Решение» и «Множество решений» — это разные вещи. Если множество решений пусто, это значит, что решений нет. Курите теорию множеств.3) © НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания). ©
Если вы определите умножение иррациональных чисел (например, число е умножить на число пи) с помощью одного лишь сложения, я буду аплодировать стоя. Компьютер оперирует преимущественно с целыми числами — в этом все дело. К тому же не стоит привязываться к стандартной алгебре на множестве вещественных чисел. Операции можно ввести по-разному.
Пионеры, комсомольцы,
Изучайте группы, кольца,
И поля, и модуля,
И делители нуля.4)© Решение есть! И оно пустое. То, что нам может не нравиться подобные результаты никого не е…(волнует), оно все равно существует! ©
Да? Предъявите его. Впрочем, написано выше. Не путайте множество и его элементы.© «Да, такое бывает, не у всякой задачи есть решение» Вообще атас! Думаю комментарии излишне. Вот они — плоды того, чему учат в школе. Любая задача имеет решение! По поводу «0 * x = 0» вообще смех, да и только. Решение не то, что существует, а вообще предоставляет полную свободу выбора. Бери любое число, оно и будет тебе решением. Ну, нет же! У нас ответ: «Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них.» Бред сивой кобылы! ©
Опять путаете. Только теперь вы путаете уравнение и операцию. Если бы изначально задача стояла в нахождении х, такого, что 0*х=0, я бы с вами согласился. Мы же говорим об операции деления на ноль.
Можно говорить, что уравнение a*x=b только если решение существует и единственно при любых a и b. Если это условие не выполняется (а оно не выполняется при a=0), то никакой операции нет и быть не может.© Как же не имеет никакого смысла, когда имеет, и еще какой! Например, если Мы будем постоянно бегать с пустым ведром от колодца к бочке, то бегай хоть 100, хоть 1000 раз — воды Мы не принесем. Уравнение это четко показывает, и имеет очень даже хороший смысл… ©
Уравнение — умеет смысл, а запись 0/0 не имеет смысла.© ы частично признаем (не признаем) полярные стороны. Другими словами «бесконечность» числом считать не принято, а вот ноль (как было замечено «ничто») числом мы считаем. А если так, то чего же мы тогда хотим? ©
Дайте определение бесконечности, если хотите считать ее числом.Ответить
-
«По поводу «0 * x = 0″ вообще смех, да и только. Решение не то, что существует, а вообще предоставляет полную свободу выбора. » Свобода выбора не есть решение.
Ответить
-
«Опять путаете. Только теперь вы путаете уравнение и операцию. Если бы изначально задача стояла в нахождении х, такого, что 0*х=0, я бы с вами согласился. Мы же говорим об операции деления на ноль.» Путаешь ты. Операция деления определена именно так: делением называется операция, обратное умножению. Что эквивалентно определению: деление есть не элементарная операция решения уравнения вида x*a=b, где a — делитель, а b — частное.
Ответить
-
«Как же не имеет никакого смысла, когда имеет, и еще какой! Например, если Мы будем постоянно бегать с пустым ведром от колодца к бочке, то бегай хоть 100, хоть 1000 раз — воды Мы не принесем. Уравнение это четко показывает, и имеет очень даже хороший смысл… ©
Уравнение — умеет смысл, а запись 0/0 не имеет смысла.» Наоборот. На дроби 0/0 построена четверть теории пределов. Три другие четверти теории пределов построены на произведении 0*0, разности бесконечность-бесконечность и дроби бесконечность/бесконечность. А уравнение 0*x=0 смысла не имеет.Ответить
-
На любом компьютере обязательно реализованы операции с действительными числами. Иначе это не компьютер. Вот целые могут и не поддерживаться, например, ZX SPECTRUM целых не знает вовсе. При этом он на процессоре Z80, который, наоборот, не знает чисел с плавающей точкой.
Ответить
-
Spectrum умеет только целочисленную арифметику, без деления и умножения. Реализация вычислений с вещественными числами (или fixed point) — целиком на плечах программиста.
Ответить
-
-
-
0x000000
dvaman
07.07.2010
09:21
Ответить
Простите, не мог пройти мимо вашего комментария.
>> прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания).
Во-первых, все зависит от архитектуры компьютера. Допустим, мы говорим про IA-86 или x86 для простоты. Процессоры этой архитектуры умеют делать все четыре арифметические действия. Да, их можно свести к двум, вы правильно заметили, и есть архитектуры, где это действительно так. Вот только сложение и вычитание производится операцией сложения с помощью прямых и обратных кодов. А умножение и деление более сложной последовательностью из сложений и побитовых сдвигов. Побитовый сдвиг ничего не вычетает, грубо говоря, он делит либо умножает исходное число на основание системы счисления. Для двоичной сс после одного сдвига число либо будет увеличено на 2 либо уменьшено на 2.>> К примеру, в программировании эта проблема решена. Мы будем делить пять на ноль, мы получим самое большое число max_value.
Да, проблема решена очень давно, но не так. В большинстве случаев, при делении на ноль будет либо вызвано прерывание процессором (для x86 это будет нулевое прерывание), если деление происходило с помощью него, либо аналог ошибки от среды исполнения. Min и Max_value в большинстве императивных языков — это ограничение на тип переменной (какие значение она может принимать в памяти), деление на ноль тут вообще не причем. Для «операций» с бесконечностью, в некоторых языках есть типы Inf и -Inf. Однако опять же повторюсь, что обычное деление на ноль в программировании подразумевает генерацию некого уведомления программисту или пользователю и штатной ситуацией не является ни на железном ни на программном уровне.Ответить
-
Inf и -Inf — не типы, а константы.
Ответить
-
-
Замечу, что в современных компьютерах все немного сложнее.
Деление на ноль целочисленного значения приведет к так называемому исключению, т.е. программа рухнет.
В случае с числами с плавающей точкой, деление на ноль даст как раз +inf, т.е. то самое «очень большое число».
А если поделить ноль на ноль, то результат будет еще интересней: получится NaN. Расшифровывается это как «Not a Number». И результат вычислений, в которых принимает участие NaN, не определен.Ответить
-
int числом не является. Это бесконечность.
Ответить
-
«А если поделить ноль на ноль, то результат будет еще интересней: получится NaN. Расшифровывается это как «Not a Number». И результат вычислений, в которых принимает участие NaN, не определен.» Не важно, что оно так «расшифровывается», а int — нет. Не числа обе всё равно. И на самом деле nan значит «не определённость». В математике она не тождественна бесконечности.
Ответить
-
-
Нет. Уравнение может не иметь решений. И бред не имеет смысла.
Ответить
-
Пустыми бывают только множества, а не решения.
Ответить
-
«НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания).» НЕ БЫВАЕТ компьютеров, умеющих только складывать. И умножение на дробь не эквивалентно какой либо серии сложений. Кстати, сдвиг разрядов — это как раз умножение в чистом виде. Но только на степень основания системы счисления.
Ответить
-
«Да, такое бывает, не у всякой задачи есть решение»
Вообще атас! Думаю комментарии излишне. Вот они — плоды того, чему учат в школе. Любая задача имеет решение!» Ну реши задачу: найти действительное значение угла, при котором синус равен четырём. Комплексный результат не не нравится, а не допустим согласно типу искомой величины. Задача вычисления арксинуса ведь может быть подзадачей в задаче построения треугольника с заданным отношением катетов, а треугольник с комплексным углом при вершине построить нельзя.Ответить
-
Ноль и бесконечность не могут стоять по одну сторону. Вот есть у тебя карман, в нём могут быть деньги. Я у тебя спрашиваю: СКОЛЬКО у тебя денег? А ты мне: у меня их совсем нет. Это ответ на вопрос сколько, то есть количество. А количество выражается только числом. А с бесконечностью этот фокус не пройдёт. И отрицательное число — это тоже количество. Есть Довгань, у него могут быть деньги. Его спрашивают: СКОЛЬКО у Вас сейчас? А он: я ещё и должен столько то миллионов. Это ответ на вопрос сколько, то есть количество. Количество может быть и дробным, но не в случае денег. Сложно объяснить, как с количеством соотносятся мнимые и гиперкомплексные числа, но они хотя бы однозначны, а это свойство числа. Но если сложить две бесконечности, то бесконечность получится только одна, а если одну бесконечность из другой вычесть, то можно получить сколько угодно, включая бесконечность. Бесконечность не однозначна. А ноль однозначен.
Ответить
-
«К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность».» Нет. Во-первых MAX_INT. А во-вторых оно определено одновременно с inf. MAX_INT инт конечна, а int — нет.
Ответить
-
«Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо.» Нет. Можно получить исключение, его низкоуровневый аналог, или inf. Но ни какой MAX не получится. Кстати, MAX_INT-MAX_INT==0, а inf-inf==nan.
Ответить
-
-
Нет. Ноль — тоже число. И число ни какого отношения к наличию не имеет. Наличие и отсутствие — это флаг. А число — это только количество.
Ответить
-
А вот что получается, когда это «нельзя» не признается http://piramyd.express.ru/disput/lebedev/h-func.htm
Ответить
Вообще-то есть тогда только сложение Потому как умножение это n раз повтореное сложение.
3*3=9
3 раза по 3 сложить вот и 9 будет О_о
Ответить
-
Это верно только для чисел. В математике операции «сложения» и «умножения» могут быть определены над самыми разными объектами, например, матрицами или функциями. Для них «умножение» совсем неравно «сложению» X раз.. Да и трудно понять сколько раз нужно «прибавить», скажем, одну матрицу к другой..
Ответить
-
Мы сейчас обсуждаем только скалярные величины. А для величин других типов можно и сложение определить иначе.
Ответить
-
-
Попробуйте pi*exp(1) выразить через сложение. exp — экспонента, то есть степень основания натурального логарифма. Или выразите через сложение, причём, не аргументов, а самих логарифмов ln(2)*ln(10).
Ответить
давайте уравнение 0*х=0 сведем от умножения к сложению???
у древних народов ваще никаких нолей не было, хотя были предпосылки к отрицательным числам, и трактовались они по бытовому — «кто кому должен», а если никому не должен — так и нет никаких отношений — ноль искусственно придумали, и он в операциях арифметики ваще присутствовать не должен — только башку засоряет))))
Ответить
-
Полностью согласенн.
Кто то вставил ноль в уравнение и все. Интересно, а если бы в математике не было ноля, как бы тогда она развивалась? Может и не было бы всяких этих неопределенностей и всяких там математических загадок? И тогда все проще было бы описать?Ответить
-
© давайте уравнение 0*х=0 сведем от умножения к сложению??? ©
В смысле?© у древних народов ваще никаких нолей не было… bla-bla-bla ©
А также у «древних народов» не было электричества, лазеров, ракетных двигателей, ядерного оружия и канализации — и что? Это значит, что все вышеперечисленное — бесполезно?© и трактовались они по бытовому — «кто кому должен» ©
Бытовое, называемое также наивным, понимание чего угодно — главная проблема людей, далеких от науки, при этом любящих о ней порассуждать.
Скажем, математическая теория хаоса, теория интегрирования дифференциальных форм, дифференциальная геометрия, теория функций комплексного переменного, аксиоматическая теория вероятностей — все это не имеет с бытовыми неурядицами ничего общего, однако тем не менее с успехом используется на практике. Это раз. Во-вторых, если определить отрицательные числа и не определять нуля, то вместо деления на ноль возникнет другая проблема: 12-12 равно чему? Т.е. нельзя вычитать одинаковые числа и складывать противоположные. Где выигрыш?Ответить
-
Ноль был как пустой карман. А отрицательных чисел как раз не было. Был долг, но даже умножать долг на долг ни кто не умел. Даже целый долг на целый долг. В том виде, как долг понимался тогда, если каменотёс должен охотнику 2 шкурки, а охотник должен две шкурки собирателю, а собиратель должен 2 шкурки каменотёсу, то они все трое должны друг другу. По-современному же они ничего друг другу не должны, так как могут взаимозачесть свои долги в ноль, всего лишь выяснив, что каменотёс, которому должен собиратель, — это тот самый каменотёс, который должен охотнику, охотник, который должен каменотёсу, — это тот самый охотник, которых должен собирателю, а собиратель, которому должен охотник, — это тот самый собиратель, который должен каменотёсу.
Ответить
Да..интересно)))Если чесно в свои 15 лет никогда на эту тему не парилась)))А оказывается всё не прото так)))
Ответить
Толковая статья. Однако, лучше вводить операции так: a-b=a+(-1)*b, и тогда все становится на свои места. Аналогично: a/b=a*b^(-1). Т.е. вводить не обратные операции, а определять «число, которое обратно данному относительно операции сложения или умножения». Тогда это будет совпадать с аксиоматическими определениями теории чисел.
***
И, кстати, корень из -1 — это бессмыслица. Под корнем не может стоять отрицательного числа. Таков уж сам символ корня. А вот, a^2 = -1 записать можно. Но это уже будет не привычное нам пространство чисел R, а R^2, где все немножко по-другому.
Ответить
-
AMapyaK
valkoivo
27.01.2009
17:51
Ответить
© И, кстати, корень из -1 — это бессмыслица. Под корнем не может стоять отрицательного числа. ©
Может. Другое дело, что без дополнительных слов корень из любого числа — бессмыслица, ибо на комплексной плоскости для любого числа a (кроме нуля, опять же) найдется ровно n таких чисел b, что b^n=a. Не зря ведь даже в вещественном случае вводят понятие арифметического квадратного корня.© Но это уже будет не привычное нам пространство чисел R, а R^2, где все немножко по-другому. ©
Не просто R^2, а R^2 с особым произведением векторов, которое и делает его полем комплексных чисел.Ответить
-
«И, кстати, корень из -1 — это бессмыслица. Под корнем не может стоять отрицательного числа. » Бред.
Ответить
Есть два замечания по поводу статьи:
1. В мат анализе никто не научит делить на ноль.
Выражение «неопределенность вида 0:0» является жаргонным названием предела дроби, чисслитель и знаменатель которой стремятся к нулю.
И еще решение уравнения 0*х=0 это х — любое число и оно вполне имеет смысл в алгебре например (когда реч идет о всяких там ядрах операторов, пространствах «натянутых» на решения и т.д.).
2. Вопрос почему на ноль нельзя делить, а вычитать ноль можно — не логичен. У дотошного читателя скорее должен возникнуть вопрос, а почему можно вычитать 1, а на ноль делить нельзя (1 — нейтральный элемент относительно умножения, 0 — нейтральный элемент относительно сложения).
Ответить
Спасибо, Александр. Вот, если бы всегда на вопросы отвечали человеческим языком, а то пишут всякие непонятные слова (определения) на своем заумном жаргоне, а ты как идиот над сносками паришься.
Ответить
Очень жаль, что комментарии на «Элементах» не модерируются. Господа, сайт хоть и научный, но все такие еще и популярный. Прежде чем писать свой довод, задумывайтесь, пожалуйста, насколько адекватно Ваше объяснение и понятно для людей не ученых, а просто интересующихся.
Для удовлетворения личных амбиций, уверен, существуют тематические форумы.
Ответить
Читая все комментарии, задаюсь я вопросом: «Тема-то интересная, но до каких пор можно отвечать на этот вопрос?» Ответов так много, что мне их хватило на долго. А вопрос про деление на ноль в школе остается простым, ответ всегда будет один — нельзя. Спасибо тем, кто загрузил меня. Оканчивая 11 класс, было приятно узнать что-то новое, кроме «нельзя»
Ответить
-
aqualix@mail.ru
DaVinci
21.03.2008
12:55
Ответить
Деление на ноль это математическая метафизика. В алгебраическом пространстве на ноль делить нельзя. В пространстве в котором операция деления на ноль, допустим закреплена как x/0=1.75 это вполне возможно. Я создаю свой мир и в моем мире деление происходит таким образом. Могу в нем задать и появление объектов посредством произнесения слова. Параллельные пространства. Во сне человек может оказаться в подобном пространстве и при определённых условиях оно будет казаться ему объективной реальностью. Сон другое пространство.
Если взять пространство в котором на ноль можно делить с определённой вероятностью, т.е допустим в 75% операций деления на ноль мы будем получать случайное число, в 25% будет ответ «делить на ноль нельзя».
Получим множество ответов(на ноль делить можно, на ноль делить нельзя). В статье обсуждалась арифметика, относительно неё на ноль делить нельзя, автор в действительности сказал, что это не имеет смысла в арифметике. Математика очень интересная наука, можно встретить числа бесконечно стремящиеся к нолю, бесконечность и ноль в одном флаконе).
Ответить
-
А в институте ещё объяснят, как много раз сложить ноль с нолём и в итоге получить не ноль.
Ответить
Попробую представить свое видение данной проблемы. Математика, как и любая другая наука была изначально создана, можно сказать, как формализованный язык описания мира в котором мы живем, с целью его понимания. А потому, она может допускать некоторые условности, упрощающие это описание. Одной из таких условностей является ноль. А поскольку человек создал этот язык, эту модель мира, то не он ли обладает свободой (ограниченной) устанавливать в ней свои правила? Так есть ли смысл ставить под сомнение запрет на деление на ноль, если это, возможно, просто правило введенное создателем языка?
Ответить
Приношу свои извинения, если подобный комментарий уже встреался, но слишком их много (и одно, да по тому же), возможно, что и пропустил.
Но…
Я разделяю такую точку зрения (к которой пришел сначала экспериментально, а только потом убедился, что так оно, в ппринципе, и есть).
Операция деления — есть суть операция последовательных вычитаний делителя от делимого, а частное — есть суть — количество итераций, проведенных до остатка не превшающего делителя.
Т.е.
10:3 =
шаг 1. 10-3=7
шаг 2. 7-3=4
шаг 3. 4-3=1
т.о. имеем частное = 3 (количество шагов) и остаток =1
а что с нулем?
1:0=
шаг 1. 1-0=1
шаг 2. 1-0=1
…
шаг N 1-0=1
— отнимаем последовательно до бесконечности, вот и выходит, что решили школьникам просто голову не морочить «перевернутой восьмеркой».
Ну, и попутно про вычитание: я своему чаду объяснил так 10-4 = 10 + (-4)
и на этом экскурс «в дебри» закончил.
Ответить
-
самое удивительное, что вчера засыпая, думал примерно о том же :)))
———-
моя теория такова:
существует множество бесконечностей, бесконечное множество
нельзя приравнивать бесконечность к бесконечности, можно лишь сказать, что вот эта восьмёрка, повёрнутая на пи-пополам — ТОЖЕ бесконечность (принадлежит множеству бесконечностей), а не РАВНА любой другой бесконечности
это необходимо принять за аксиому, потому как:
оо + 1 (бесконечность плюс один) — это тоже бесконечность, равно как и просто оо
оо + 2 — это бесконечность
…
оо + оо — это бесконечность (а не «равно бесконечности»)
исходя из такого рассуждения (интересно, а как его вообще можно оспорить?), делаю следующий вывод (повторяя предыдущего «оратора»):
1/0 = ?
шаг 1. 1-0 = 1
шаг 2. 1-0 = 1
… (операции одинаковы, ничего не меняется от первой операции ко второй, а следовательно — не изменится и до бесконечности)
шаг оо. 1-0 = 1
отсюда вывод, что 1/0 = оо + 1, что тоже является бесконечностью, равно как и 5/0 = оо + 5
последнее — для тех, кто утверждает, что получается алогизм, когда при сокращении единица становится равна пятёрке…
———-
«решили школьникам просто голову не морочить «перевернутой восьмеркой»»
а кто решил-то? почитать тему, так можно найти ярых противников деления на ноль — вот такие же и «решили», потому что сами так считают… тут дело вовсе не в слабости детского восприятия или фантазии — это скорее дело во взрослых
———-
и вообще, на делении на ноль можно и не останавливаться (хоть лично я и люблю эту тему) — ведь есть ещё интересные вещи типа 0/0, оо/0 и т.п. :)))Ответить
-
Если 10/3 означает, что нужно сделать 3 шага вычитания тройки из десятки, разве 1/0 означает, что нужно сделать оо шагов вычитания нуля из единицы?
Скорее это означает, что нужно сделать 0 шагов вычитания нуля из единицы. В результате, по идее, 1 должна стать нетронутой единицей. В смысле, все остальные числа в результате деления на все остальные числа остаются тронутыми, а в результате деления на 0 все остальные числа становятся нетронутымиОтветить
-
С какого перепугу?
Ответить
-
-
В статье чтобы осветить один вопрос приведено несколько доводов в свою очередь вызывающих разные вопросы. Дети, не ленитесь, учите матчасть!
Ответить
К единственному ответу на этот вопрос Вы не приблизитесь, пока не начнете рассматривать понятие «ноль» в рамках какой-то определенной теории! В зависимости от системы аксиом, на которой строится Ваша теория, Вы можете делить на ноль, вычислять 0^0 и т.д. Вопрос в том, можно ли с пользой применить такую теорию на практике?
В школах изучаются теории, в которых на ноль делить нельзя. Ваши предложения по введению в эти теории понятий бесконечности и неопределенности просто строят теорию, в которой уже делить на ноль можно, но это другая теория, которую в школе не изучают, да это и не нужно!
Добавьте в систему аксиом геометрии Лабочевского аксиому параллельности прямых, и получится геометрия Евклида.
Как ответить на вопрос «Чему равна сумма углов в треугольнике»?!
Одни ответят — 180 градусов! — и будут правы.
Другие возразят — нет! Треугольник, который строится из 2 меридиан, пересекающихся под прямым углом, и экватора, имеет сумму углов 90*3=270 градусов! — и тожке будут правы!
Так что правы и те и другие, к чему спор?
Теперь, что касается вопроса — «Почему» на ноль делить нельзя?
Сам вопрос уже с подвохом.
Ноль просто не входит в область определения знаменателей операции деления. Почему нельзя делить на фиолетовый? По той же причине! Просто фиолетового нет на числовой прямой, а ноль есть, и это сбивает с толку.
Для тех, кто хочет делить на ноль — введите в множество, в которое вы хотите ввести бесконечность и неопределенность еще и фиолетовость — возможно эта новая теория будет революционным скачком в науке, но к теориям, изучаемым на данный момент в школе и ВУЗах отношения иметь не будет.
Ответить
-
Ноль определён однозначно. И ни какие «левые» теории здесь не причём.
Ответить
-
-
Не верь, если себя не уважаешь. Ни кто же не заставляет.
Ответить
-
Уважаемый !ё!, ответ на детский вопрос — не лучшее место для троллинга. Пожалуйста, доказывайте, что х*0 = х*1 = х, где-нибудь еще. Вам пока всего лишь включена премодерация, но продолжение банкета = бан (судя по всему, для вас уже не первый). И это обсуждение скоро будет стерто — если кто-то хочет его скопировать, у вас есть примерно сутки.
Ответить
-
-
А кто сказал, что на ноль делить нельзя? этому учат на уроках арифметики в начальных классах… А людям с высшим образованием, хотябы отдаленно слышавших о теории пределов, товарище Лопитале и всем таком, должно быть понятно, что деление на 0 в полне нормальная математическая операция, которая в ответе дает бесконечности различных порядков. А по поводу статьи могу сказать следующее: никакого отношение она к математике не имеет, скорее к эпистолярному жанру литературы, я, к примеру, могу путем подобных софистических рассуждений доказать, что единственная арифметическая операция — возведение в степень, а все остальные производные от нее… ))
Думаю, перед тем как писать подобную чушь, автору нужно было хоть немного почитать историю развития математики и историю теории множеств…
Ответить
Из научного фольклора: «Необходимость делить на ноль выглядит катастрофой в глазах математика и может даже вызвать лёгкое смущение у физика-теоретика.»
Ответить
По моему, кол-во комментариев само по себе говорит о том, что…но давайте без оскорблений.
Лично я нашёл для себя удобный выход. Числа — это числа, а ноль и бесконечность — это ПРОЦЕСС. Нет ноля и бесконечности — это пределы. То есть какое бы вы не выбрали ЧИСЛО, можно НАЙТИ число большееменьшее данному. Именно поэтому ноль и бесконечность -процесс. Им вообще нечего делать в математике. Это исскуственные формации. Как темная материя, возможно. Так что, вопрос, почему делить на ноль нельзя, сродни вопросу «что общего между цифрой 8 и зелёным цветом». Это просто несовместимые понятия. Всё равно что прибавить к одному метру одну секунду. Что получится? ДА НИЧЕГО! А вы тут развели дурацкие дебаты. Чуть ли не докторскую защищаете.
Типичные математики :)))))
Ответить
-
Бред. Ни ноль, ни бесконечность с процессами даже близко не валяются.
Ответить
-
-
Наоборот, «бред» — самое НЕ любимое моё слово. Из всех, которые я в принципе употребляю.
Ответить
-
-
-
И уж или нечего делать в математике, или искусственные формации. Стремиться, кстати, величины могут к чему угодно. Так что, числа вообще не существуют?
Ответить
-
Уж или о своём, или от твоём бреде.
Ответить
-
Мне когда-то объяснили примерно так (от меня надо было срочно отвязвться): дали несколько спичек и сказали «а теперь раздай их пустому месту так, чтоб было поровну», я сказала «но тогда все спички у меня будут», на что мне ответили «но ты ведь не пустое место».. и я ушла умножать на бесконечность))))
Ответить
mikheyev.sergey


Ответить
Внимательно всё прочитал, и решил: делить на ноль нельзя, но если очень хочется, то можно. В таком случае, придётся расширить число математических сущностей — существует бесконечное число нулей и бесконечное число бесконечностей различных порядков, которые не равны друг другу, и которые можно перемножать и делить друг на друга. Придётся смириться с парадоксом бесконечности – часть равна целому. Например, число всех чётных чисел равно числу всех целых чисел. Будьте осторожны, применяя эту теорию на практике. Мавроди не учёл, что число вкладчиков финансовой пирамиды отлично от бесконечности, и за конечное время был привлечён к уголовной ответственности, за свою математическую ошибку.
А дискретная топология и математика конечных множеств, скучна и банальна, также как наша реальная дискретная и конечная вселенная. Прошло примерно 30 лет как учёные рассчитали максимальный и минимальный размер в нашей вселенной, долю тёмной энергии (75%), структуру «суперструн» (вихри в сверхтекучей жидкости), начальную и конечную энтропию и температуру нашей вселенной (реликтовое излучение). Нас всех посчитали!!! Давно известно, как и когда разрушится пространство нашей вселенной и во что, оно превратится. Просто, скучно, грустно, и никому не нужно.
Ответить
-
taras
mikheyev.sergey
11.10.2017
18:31
Ответить
Ноль существует ровно один. Он даже в октанионах тот же самый. А нуль-вектор — это уже не ноль. Как и нуль-матрица.
Ответить
В математике есть такое понятие, как бинарная операция. В каждом конкретном случае строго определяется множество элементов, над которыми выполняется операция, и указывается правило, как по двум элементам можно вычислить результат операции.
Математики допускают, что для некоторых элементов результат операции может быть не определен. Но если результат есть, то он должен быть один, и обязательно должен принадлежать исходному множеству элементов. На таком определении операции построена вся арифметика, теория групп и много еще чего.
Конечно, можно определить или привести свой пример операции, у которой более одного результата. Но это будет не операция, а что-то другое.
Что касается фразы «на ноль делить нельзя», то она математически не корректна, потому что в этой фразе непонятно что означает слово «нельзя». Почему нельзя ?! Потому что учитель не разрешает ? Или потому, что если начать делить, то что-то нехорошее произойдет, например, компьютер сломается, если делить на компьютере ?
Математический корректная формулировка такая: на множестве целых чисел для любого целого числа N результат операции N : 0 не определен.
Кстати, в невозможности делении на ноль нет ничего уникального. В математике можно найти очень много других операций, которые не всюду определены. Например, если мы возьмем множество ПОЛОЖИТЕЛЬНЫХ целых чисел и рассмотрим на этом множестве операцию вычитания, то можно привести сколько угодно примеров, когда результат вычитания не определен: 1-2, 10-20, 100-105 — во всех этих случаях результат вычитания не определен, потому что получается отрицательное число.
Ответить
Если посмотреть на процесс решения уравнений, то там используются эквивалентные преобразования, то есть исходное уравнение заменяется другим, более простым, и так по цепочке, пока не получим все решения.
Одно из эквивалентных преобразований — это умножение или деление обеих частей уравнения на одно и то же выражение. И вот тут есть правило, что умножать или делить можно на что угодно, но только не на ноль. На ноль делить обе части уравнений нельзя! И умножать на ноль нельзя! Здесь под «нельзя» понимается то, что если это сделать, то уравнение будет решено неверно: например, могут появиться лишние корни.
Есть также чисто житейское соображение почему на ноль делить нельзя
Например, если на экзамене в ВУЗ вы будете решать уравнение (x*x -1)/(x-1) = 2 и не сделаете отметку, что x не равно 1, то есть забудете правило, что на ноль делить нельзя, затем поделите числитель и знаменатель на (x-1), получите x+1=2, то есть напишете x=1, то вы дадите неверное решение.
Таким образом, на ноль делить нельзя еще и потому, что можно получить плохую оценку и не поступить
Ответить
-
Как Вы лихо многочлен на многочлен делите. Там вообще то левая и правая части умножаются на (x-1).
(x*x-1)/(x-1)=2
(x*x-1)=2*(x-1)
x*x-1=2*x-2
x*x-2*x+1=0
D=0
x=1.
И только ПОСЛЕ ЭТОГО результат сравнивается с областью определения левой части исходного уравнения. Точнее он вообще подставляется в исходное уравнение для проверки решения и обнаруживается нулевой делитель, из чего делается вывод об отсутствии решений.Ответить
-
Taras написал:
<
Как Вы лихо многочлен на многочлен делите. Там вообще то левая и правая части умножаются на (x-1).
>
Вы забыли, что x*x-1 равно (x-1)(x+1). Так что ничего лихого в делении на (x-1) нет.Ответить
-
Нет. Это Вы забыли, что любому школьнику проще запомнить алгоритм, чем таблицу. Тем более чем найти в ней по памяти столбец по значению ячейки на его пересечении со строкой, а не наоборот. А у Вас сразу результат деления многочлена на многочлен без каких либо операций для его получения. Вот в этом и лихость. Результат же я не оспариваю.
Ответить
-
-
Кроме того, Вы, taras, основательно подзабыли курс школьной алгебры.
Если вы умножили уравнение, зная (из области определения) что множитель ненулевой, то, получив окончательное решение (решения), ничего проверять НЕ надо.
Лишние решения могут появиться при возведении обеих частей уравнения в квадрат. Вот тогда надо проверять.
Если вы извлекли квадратный корень из обеих частей уравнения, то чтобы не потерять корни, надо будет решать отдельно ДВА уравнения.
Ответить
-
«Кроме того, Вы, taras, основательно подзабыли курс школьной алгебры.» В отличие от Вас нет. Откуда я заранее знаю, что множитель не нулевой, если он содержит искомую переменную? Решения положено проверять подстановкой ВСЕГДА. То, что многие ленятся, решая уравнения, допускающие абсолютно все значения искомой величины, к правилам ни как не относится. Реальные же задачи всегда ещё и ограничения имеют. Соответственно решения ещё и на них должны проверяться. Единственное, когда проверка не требуется, — это если в методе бисекций f(c)=0.
Ответить
-
Taras написал: «Откуда я заранее знаю, что множитель не нулевой, если он содержит искомую переменную? Решения положено проверять подстановкой ВСЕГДА. «
Да уж …
При решении уравнения сначала выписывается область определения неизвестного (чтобы не было деления на ноль, чтобы у логарифма был строго положительный аргумент и т. д.).Далее вы делаете постепенные преобразования уравнения.
На каждом шаге вы УЖЕ должны четко знать, что либо число корней не изменится, либо их может стать больше, либо их может стать меньше. Если вы этого не знаете, значит вы не понимаете самой сути решения уравнений.
В частности, если вы умножаете обе части уравнения (или делите) на какой-либо множитель, то прямо на этом шаге вы УЖЕ должны быть уверены, что он не нулевой. Для такой проверки у вас есть область допустимых значений.
Если в процессе решения у вас все преобразования были эквивалентными, то есть вы знаете, что не может быть потерянных корней и не может быть лишних корней, то и проверять найденные корни НЕ надо.
Я тут имею ввиду, что не надо делать проверку в тетрадке, которую вы преподу сдаете. Ну, либо можно написать, что проверять решения не надо, так как все преобразования были эквивалентными.Совсем другое дело, что для себя лично, где-нибудь на промакашке нужно обязательно проверить корни, чтобы убедится, что вы не допустили ошибку.
Ответить
-
Да хоть за выписывайтесь. ЗАРАНЕЕ НЕ ИЗВЕСТНО, ЧТО ПОЛУЧИТСЯ В ХОДЕ ВЫЧИСЛЕНИЙ, соответственно проверка на попадание в область выполняется только для почти готового ответа. Ну как почти. Когда только проверить и осталось. И обратите внимание: деление на ноль не выполняется даже в случае сокращения числителя на знаменатель, а критикую я такой ход решения только за выброшенный черновик. Потому что раскрыть то скобки и привести подобные может любой старший школьник, причём, быстр и часто в уме, а над обратной операцией может задуматься даже дипломник, тем более когда делитель задан. Об ошибке при делении многочлена на многочлен речи не было. Нулевым же знаменатель оказывается ПОСЛЕ деления. Все ограничения выписываются максимально рано, на сколько это возможно, но их соблюдение проверяется ПОСЛЕ ТОГО, КАК ПОЛУЧЕНЫ СООТВЕТСТВУЮЩИЕ ЗНАЧЕНИЯ. В случае корня квадратного одно из ограничений проверяется после того, как получено значение подкоренного выражения. Вообще в случае функции с ограниченной областью определения проверка выполняется после того, как получено значение аргумента.
Ответить
-
Taras написал :
<
ЗАРАНЕЕ НЕ ИЗВЕСТНО, ЧТО ПОЛУЧИТСЯ В ХОДЕ ВЫЧИСЛЕНИЙ, соответственно проверка на попадание в область выполняется только для почти готового ответа.
>Конечно заранее не всё известно, что получится, потому что тогда и решать бы не надо было.
Но на каждом шаге, применяя очередное преобразование уравнения, должно быть совершено точно известно по поводу корней уравнения (значения которых будут получены только в самом конце) : останется ли число корней прежним, либо могут появиться лишние корни (например, при возведении в квадрат) и тогда надо в решении сделать отметку об обязательности проверки корней, либо далее придется отдельно решать два разных уравнения (например, чтобы не потерять корни при извлечении квадратного корня из обеих частей уравнения).
Когда вы закончите решение и найдете один или несколько корней, вам нужно будет просмотреть ход вашего решения, и если в нем нет ни одной отметки о возможности появления лишних корней, то проверять найденные корни не надо.
<
И обратите внимание: деление на ноль не выполняется даже в случае сокращения числителя на знаменатель,
>
Нет, тот, кто так считает, делает грубейшую ошибку.
Сокращение числителя и знаменателя это и есть деление, и прежде, чем его провести, надо проверить по ОДЗ, что такое деление возможно<
Потому что раскрыть то скобки и привести подобные может любой старший школьник, причём, быстр и часто в уме, а над обратной операцией может задуматься даже дипломник, тем более когда делитель задан.
>
Хм, на то, что X^2-1 это (X-1)(X+1), натаскивают в пятом или шестом классе школы. Ну, хорошо, я отмечу этот момент в своем первоначальном посте.<
Об ошибке при делении многочлена на многочлен речи не было. Нулевым же знаменатель оказывается ПОСЛЕ деления.
>
Тут вы уже совсем запутались. После деления (X^2-1) на (X-1) в числителе будет (X+1), а знаменатель будет единичным, и поэтому от него в дальнейшем можно отказаться.<
В случае корня квадратного одно из ограничений проверяется после того, как получено значение подкоренного выражения.
>
Если вы имеете ввиду извлечение квадратного корня из обеих частей уравнения, то в таком случае ничего проверять не нужно. А нужно далее решать отдельно два разных уравнения, а в конце их корни нужно будет объединить в общее решение.Ответить
-
-
-
-
«Лишние решения могут появиться при возведении обеих частей уравнения в квадрат. Вот тогда надо проверять.» Проверять положено даже в том случае, если уравнение вообще не преобразовывалось. И дело, как показывает данный пример, не только в лишних решениях, но и в допустимых значениях. Кроме того, решения проверяются и на случай просто ошибки, например, на случай, D=b^2+4*a*c, или D=b^2+a*c.
Ответить
-
-
я считаю что любое действие в математике должно иметь обратное действие, так что если нельзя делить на ноль то и умножать тоже например х*0=0 следовательно обратное действие х =0:0 где х в принципе может быть абсолютно любым числом. в этой связи предлагаю относиться к нулю как к отсутствию действия будь то сложение или умножение. Либо предлагаю определить 0 как минус бесконечность плюс бесконечность и полное отсутствие у нуля стремления к действию.
Ответить
-
Штейн написал: «я считаю что любое действие в математике должно иметь обратное действие»
Согласен, что отсутствие обратного действия может вызвать у школьника недоумение.
Тут всё дело в том, что школьникам дается только малая часть математики. Математика очень трудная наука, и поэтому математики постоянно стремятся как можно больше упростить свои определения и доказательства.
Уверяю вас, что если бы от вашего предложения была хоть малейшая польза, то математики давно бы уже им воспользовались.
На самом деле, если последовать вашему предложению, то количество «непоняток» с нулем возрастет многократно.
Ответить
-
Вы совершенно напрасно припутываете бесконечность к числам. Ноль, 10, -3.5 — это всё числа. А бесконечность числом не является.
Понятие беконечность возникает не в теории чисел, а в математическом анализе. Причем и тут строго говоря, беконечность как математический объект не существует. Нет такого объекта как бесконечность в математике!
Когда математики говорят, что, например, сумма ряда стремится к бесконечности, то они просто имеют ввиду, что рано или поздно сумма ряда превысит любое наперед заданное число. Говорить при этом, что сумма ряда равна бесконечности — это неточность, так иногда физики выражаются. Правильно говорить, что сумма ряда стремится к бесконечности, или что ряд расходится. Иными словами, здесь нигде нет бесконечности как какого-то вполне определенного числа или математического объекта.
Ответить
-
Вот только есть ещё бесконечность минус бесконечность и бесконечность, делённая на бесконечность. А ещё интеграл определён как бесконечная сумма бесконечно малых слагаемых. Но при этом многие интегралы имеют вполне строго определённые значения. Так что, интеграл тоже теперь не математичен? И физики так не выражаются, физики как раз обожают такие преобразования, при которых бесконечность изгоняется.
Ответить
-
taras написал :
<
А ещё интеграл определён как бесконечная сумма бесконечно малых слагаемых.
>
Это грубое упрощение. Ничего подобного в определении интеграла нет.На самом деле интеграл (точнее, определенный интеграл) определяется через предел последовательности интегральных сумм.
Ответить
-
Энто с каких же пор? «На самом деле интеграл (точнее, определенный интеграл) определяется через предел последовательности интегральных сумм.» Во-первых не путайте определение с выводом. А во-вторых к чему ж эта сумма ещё может стремиться при deltax, стремящемся к нолю?
Ответить
-
С каких пор?
Во-первых, всегда так было (ну, лет двести уже, как минимум). Возьмите любой учебник по матану и почитайте. Или хотя бы в Википедию посмотрите.
Во-вторых, если интеграл существует, то каждая последовательность интегральных сумм будет сходиться к значению интеграла.
Ответить
-
А ничего, что как раз ни когда не было?
Ответить
-
-
-
-
Taras написал :
<
Вот только есть ещё бесконечность минус бесконечность и бесконечность, делённая на бесконечность.
>
А это и вовсе математически некорректные выражения. Так говорят некоторые преподы на первом курсе ПТУ, причем они имеют ввиду вовсе не какие-то математические объекты, а просто разделы из задачника.Например, мы ищем предел от деления двух функций в некоторой заданной точке, причем каждая из этих функций стремится в этой точке к бесконечности. Вроде бы имеем бесконечность делить на бесконечность?
Но тут все зависит от самих функций. Предел от деления может быть каким угодно: конечным числом, уходить в плюс бесконечность, уходить в минус бесконечность, и даже уходить просто в бесконечность, и, наконец, предел может вообще не существовать.
Пример : f1(x) = 1/2x, f2(x) = 1/3x. Обе функции стремятся к бесконечности в точке ноль, но их частное всегда равно 1.5
Еще пример : f1(x) = 1/x^2 (x^2 — это х в квадрате), f2(x) = 1/x. Обе функции стремятся к бесконечности в точке ноль, и их тоже стремится к бесконечности.
Так что выражение «бесконечность деленная на бесконечность» — это математически некорректное выражение. Если уж хочется что-то подобное сказать, то надо уточнять, например, так : O(2) деленное на O(10).
Ответить
-
«А это и вовсе математически некорректные выражения. Так говорят некоторые преподы на первом курсе ПТУ, причем они имеют ввиду вовсе не какие-то математические объекты, а просто разделы из задачника.» А ничего, что это вполне стандартные неопределённости? В ПТУ я, кстати, не был ни разу. И ПТУшные задачники ни разу не видел.
Ответить
-
«Так что выражение «бесконечность деленная на бесконечность» — это математически некорректное выражение. Если уж хочется что-то подобное сказать, то надо уточнять, например, так : O(2) деленное на O(10).» Нет. Это, например, lim x/(x^4) при x, стремящемся к бесконечности. Водится в сходимости рядов. А обозначение O() лично я видел только в контексте вычислительной сложности и расхода памяти. Бесконечности там как раз не водятся, как и неопределённости.
Ответить
-
Тарас, эта ветка началась с выяснения, есть или нет такой математический объект как бесконечность.
Так вот, такого объекта в математике НЕТ.
Число 78 есть, число пи есть, есть функции, значения которых в некоторой точке стремятся к бесконечности, а просто бесконечности нет. И бесконечность/бесконечность тоже нет.
Ответить
-
Бред. Такого объекта нет потому, что это НЕ ОБЪЕКТ. Это не отменяет того факта, что бесконечность — сугубо математическое понятие.
Ответить
-
Вот есть ноль, на него только делить нельзя, а умножать, вычитать и складывать с нолем — это пожалуйста.
С бесконечностью вообще нельзя никаких арифметических операций производить: например, нельзя умножить бесконечно на 12.34
Ответить
-
-
-
-
-
-
кто нибудь может объяснить почему при умножении на 0 всегда получается 0 ?
Ответить
-
Для любого n верны следующие выражения:
(n * 2) — (n * 2) = 0, потому что когда из числа отнимаешь его же, то получается ноль. Теперь приведем подобные:
n * (2-2) = 0
n * 0 = 0Конечно, это не строгое математическое доказательство, а объяснение. Но вы ведь и просили дать объяснение.
Ответить
-
А по-моему очень даже строго )
Здесь требуется только показать, что (-1)*n=-n, то есть что противоположное к действительному число есть то же самое число, умноженное на «-1», то есть на число, противоположное «1». Я думаю этот факт не вызывает вопросов (как например с делением на нуль). Тогда:
n+(-n)=0 (определение противоположного числа)
n*1+n*(-1)=0 (определение единицы и названный выше факт)
n*(1+(-1))=0 (дистрибутивность)
n*0=0 (ещё раз определение противоположного числа)Ответить
-
Хотя можно и проще:
n+(-n)=0_______ (определение противоположного числа)
n*1+(-n)=0_____ (определение единицы)
n*(0+1)+(-n)=0__ (определение нуля)
n*0+n*1+(-n)=0_ (дистрибутивность)
n*0+n+(-n)=0___ (определение единицы)
n*0+0=0_______ (определение противоположного числа)
n*0=0_________ (определение нуля)Ответить
-
-
Статья познавательная.
Не удержался:
По поводу компьютеров: там используется теория циклических полей, где числа это скорей «порядковые номера» элементов – после максимального значения следует минимальное (а после минимального максимальное), при этом устанавливается признак переполнения. И если в каких-то приложениях этот признак интерпретируется как запрет деления на ноль, то это проблема/преимущество этих приложений. В компьютерах проблему «решили» …по своему…
По поводу ноля: еще индейцы для обозначения единиц использовали не яблоки а «раковины с едой», а «раковина без еды» и есть ноль еды.
Ответить
-
taras
D.-.i.-.m.-.a
11.10.2017
18:56
Ответить
Бредятина. Ничего, что цифровые данные дискретны, а поля — нет?
Ответить
-
-
Переведи. Пожалей бедного ирокеза.
Ответить
-
-
А на ноль делить и нельзя. И тот, кто утверждает, будто в компьютере используется теория поля, должен знать, что такое поле. А то так можно договориться до того, что работа компа — это сепуление декавилек.
Ответить
-
-
Не путай операцию деления с выражением под знаком предела. Все операции, выполняемые для поиска значения этой дроби, выполняются над самой функцией и к алгебре каких либо чисел вообще не относятся. Даже если в основе декремент показателя, выраженного как раз числом, эта операция над показателем — лишь реализация, а сама операция — СИМВОЛИЧЕСКОЕ деление НА САМУ ПЕРЕМЕННУЮ вместо её значения. И на ноль не делят всё равно. Но это не столько сложно, сколько хитро.
Ответить
-
-
-
-
-
-
Попытка объединить философию и математику http://www.zengarden.in/filosofiya-deleniya-na-nol/ См. также комментарии
Ответить
На школьном этапе обучения все надо как-то объяснить детям, исходя из их естественного опыта. Нельзя (!!!) вводить, например, сложение из аксиом, а надо показывать, что если было два яблока, а затем добавили еще три, то теперь, если пересчитать яблоки, их окажется пять. Так как же школьникам обьяснить деление на ноль? Может так?: Если вы делите на маленкое (положительное) число, которое много меньше единицы, то в результате получается большое число. (1:0.01=100) Если делитель ещё уменьшить, результат ещё станет больше. (1:0.00001=100000) А при делении на самое маленькое число результат получается больше всех чисел, но такого числа, которое больше всех чисел, нет, поэтому мы и говорим, что делить на ноль нельзя. — Как вы думаете, понятно и полезно ли будет детям такое объяснение?
Ответить
-
Human
TutorState.com
17.12.2011
22:44
Ответить
Вполне себе. Даже мне понятно стало )
Ответить
-
taras
TutorState.com
11.10.2017
19:01
Ответить
Именно из-за такого объяснения я и был уверен, что на ноль делить можно. Даже диссертацию защитил, будучи уверенным, что можно. Ведь бесконечность — не число и больше любого числа, а раз она может получиться при делении на ноль, то всё в порядке. И только потом мне попалось обоснование через уравнение.
Ответить
Простой но гениальный ЧЕЛОВЕК


Ответить
На самом деле всё проще! я солидарен с теми кто говорит что деление на ноль приведёт к бесконечности. во первых, если делить на число меньше целой единицы(например x/0.01) и приближать число всё ближе к нолю(x/0.00001) то в итоге будет получаться всё большее число, а теоретически поделив на ноль выйдет=бесконечность. Это я как бы для детей объяснил, а сейчас будет пример чуть по сложнее. Во вторых, если ноль умножить на бесконечность то с одной стороны можно сказать что останется ноль, а с другой стороны останется всё та же бесконечность!(тоже что сказать про стакан который на половину пустой или же он на половину полный(я согласен что в этом случае проще было бы сказать что останется ноль, а не бесконечность, потому что это означало бы прекращение каких либо вычислений и умственных процессов, но по сути бесконечность не чуть не уступает нолю)), а если быть более точным то ноль умноженный на бесконечность это=»любое число».(допустим X это «любое число») то есть 0*∞=X или 0/0=X(как было в статье) и ∞/∞=X,в этих случаях ответом будет «любое число». а если ∞*X=∞, X/∞=0 и X*0=0 так же и X/0=∞
Ответить
-
Простой но гениальный ЧЕЛОВЕК
Простой но гениальный ЧЕЛОВЕК
26.09.2011
03:15
Ответить
По моему, всё просто и перемудривать нет смысла.
Ответить
-
taras
Простой но гениальный ЧЕЛОВЕК
11.10.2017
19:02
Ответить
Бесконечность ничего ни на что делить не может.
Ответить
-
-
А как ЭТО можно умудиться не понять?
Ответить
-
-
Делить на ноль нельзя потому, что это лишено смысла… например арифметического и не только … +0 значит ничего не добавить (дать)… -0 ничего не забрать (отнять)… *0 значит обнулить — превратиь результат в 0… /0 значит поделить число на 0 частей — действие лишено смысла — вот поэтому его делать нельзя — так детям понятно — нельзя делать то, что лишено смысла…
Ответить
-
daria_dsm
gssgssgss
13.06.2013
15:53
Ответить
да,верно))) просто как все)
Ответить
-
Смысл есть всегда и во всём, например, чтобы увести от истины или обозначить новое правило игры с истиной. А смысл математики в том, что она должна отражать реальную действительность. Каждое число обозначает количество чего-то вещественного (материального) или количество каких-то действий. Смысл 0 состоит в том, что он не имеет ни вещественного наполнения, ни наполнения действиями. Но обозначить-то (записать, запротоколировать) это как-то нужно, значит нужен и 0. Про сложение и вычитание gssgssgss правильно сказал: ни дать, ни взять, а потом съехал с пути истинного. Ведь про деление и умножение можно так же сказать: ни делить, ни умножать, т.к. нуль это отсутствие действия.
Разделить на 0 это значит не делить ни на что (ни на какие части), т.е. оставить всё как есть. Ведь не делить ни на что и разделить ни на что это одно и то же. Отсюда следует, что с 5-ю ничего не нужно делать ни сколько раз. Тогда 5/0 = 5. А если не нужно умножать, то и 5*0 = 5, т.е. противоположные «не действия» подтверждают друг друга строго математически. Правда получается кажущееся противоречие с единицей: 5/1 = 5 и 5*1 = 5. Но если подумать, то и здесь нет никаких противоречий. 5/1 это значит из 5 счётных палочек сделать (сформировать) одну кучку, в которой было бы 5 палочек. Скажем палочки лежали на столе разрозненно, а мы их положили одной кучкой (в одном месте). Но на столе-то при этом осталось прежнее количество палочек, т.е. 5/1 = 5. Умножение, 5*1 это значит, что 5 палочек нужно посчитать (учесть) только один раз. Тогда 5*1 = 1+1+1+1+1 = 5.
В результате 5/0 = 5*0 = 5*1 = 5/1 = 5. И в этом так же нет никаких противоречий, т.к. единичное действие с одним и тем же наполнением означает, что с этим наполнением нужно провести такое действие, при котором наполнение не изменится. Так оно и есть. При делении на 1 мы соединили палочки в одну кучку, а при умножении на 1 мы их просто заново пересчитали, т.е. действие-то есть, но результат не изменился.
При сложении и вычитании всё несколько иначе, т.к. эти действия связаны с другим наполнением, чем то, над которым необходимо произвести действие.
А детям можно сказать просто: нуль это значит ничего не делать, т.е. при всех математических действиях числа с нулём число не изменяется. Куда ещё проще?Ответить
-
Бред. А бред ни когда не имеет смыла.
Ответить
-
withoutthetime
?ё!
07.04.2019
20:04
Ответить
Еще в школе было вот какое объяснение деления: предположим 100÷20 — это вычислить сколько в одной сотне раз по двадцать, сколько двадцаток в сотне. Ну вроде все понятно — кончно пять!
А теперь как бы расчитать сколькл в той же сотне нолей ( 100÷0)??? И мне кажется что их не то, что бы нет ( нолей в сотне) похоже что нет и самого ответа на этот вопрос!
В то же время мне не даёт покоя X×0=0 и нахождение из этого уравнения «X»!!!Ответить
-
-
taras
gssgssgss
11.10.2017
19:03
Ответить
Ну так лишено смысла, что на дроби 0/0 построена четверть теории пределов. Дробного количества частей тоже не бывает, но делить на дробь можно. Проблема же именно в самом определении операции деления. Она не самостоятельна, а введена как обратная операция, то есть её результат есть решение уравнения. А уравнение x*0=a лишено смысла.
Ответить
-
-
Нет. Вот есть у тебя лента. Ты её порезал на три части, мне отдал две. Их не может быть ни две с половиной, ни полторы. Дробной бывает доля от целого. Один кусок — четверть, другой — треть, третий — то, что осталось, то есть пять двенадцатых. Доля от целой ленты, приходящаяся на два отданных куска — семь двенадцатых. Но кусков два. Одно количество — дробное, другое — целое. «А вот осмысление физики, т.е. действительности на основе решения математических уравнений действительно не имеет смысла, т.к. смысл математики в физике, но никак не наоборот. Не так ли?» Ну разумеется смысл математики — физика. Ведь именно математика описывает физику, а не наоборот. Для того и создана. И именно поэтому в любой реальной задаче есть ограничения и на типы величин, и на их значения. Например, если уравнение описывает высоту полёта дирижабля, то решение не только может быть только действительным, но и не может ни быть отрицательным, ни превышать толщину атмосферы. Если тангенс описывает отношение расстояния к базе дальномера, то угол может быть только действительным в диапазоне от ноля до ставосьмидесяти градусов, а аргумент — половина угла. Соответственно тангенс не может превратиться в отношение двух экспонент. И именно поэтому имеет смысл именно осмысление и физическая интерпретация решений математических уравнений.
Ответить
-
-
Нет. Это ты путаешь два одинаковых и два РАЗНЫХ куска. Один — одна треть, но второй то — ЧЕТВЕРТЬ.
Ответить
-
» Вы хотели сказать, что дробных частей не бывает. » Нет. Части бывают ТОЛЬКО ДРОБНЫМИ. Но их количество при этом бывает только целым. Может быть четверть, но не полторы четверти. Запись 1,5/4 возможна. Но означает она не полторы четверти, а три восьмых. Это меньшие части. Нельзя отдать полтора куска ленты. Можно отрезать меньшие куски и отдать два. Математически бывают и трёхэтажные дроби. Но физического смысла в них уже нет.
Ответить
-
-
-
Вот и приведите к целому числителю. Это ведь не сложно.
Ответить
-
-
Господа, отправьте малограмотную к тому посту, где определяется 0 — как число, как его отсутсвие или как ЧТО (так ноль-это число или нет вообще?!!!)? Вопрос блондинки: с точки зрения двоичной системы я понимаю про «наличие отсутствия» и «отсутствие наличия» (здесь сарказм), ну то есть, почему 1 и 0 -это метафизические противоположности, но как тогда быть с -1 и всемы вытекающими отовсюду последствиями????Повторяю:»я гуманитарий»!!!!
Ответить
-
taras
Jill2zso5i
11.10.2017
19:10
Ответить
Определение: нолём называется такое число, что сумма его с любым числом равна второму слагаемому. Ноль это число, означающее отсутствие, что роднит его со сброшенным флагом, но сброшенному флагу противопоставляется установленный флаг, означающий просто факт наличия, а не ноль имеет бесконечное количество вариантов, каждый из которых — конкретное количество.
Ответить
-
-
Нет. Отсутствие количества — это совсем другое. А ноль — это количество. Вот есть у тебя карман и карман этот пустой. Если он пустой, то денег в нём ровно ноль. А теперь я у тебя спрашиваю: СКОЛЬКО денег у тебя в кармане. Ты же отвечаешь, что их там нет вовсе. Это ответ. Теперь другая ситуация. Вернулись я в прошлое и спрашиваю свою краснокожую прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабку: а сколько у тебя автомобилей в гараже? Она НЕ МОЖЕТ ответить, потому что само понятие «автомобиль» ещё не придумано, соответственно нет и количества автомобилей. В этом случае их не ноль, а брошен флаг их существования. Противоположность нолю — не ноль, противоположность сброшенному флагу — установленный флаг. Но не ноль — это и 1, и 2, и 120, и 390, и 8. И каждое значение отмечается своим числом. А установленный флаг — это просто есть. Вот есть и всё без указания количества. То есть если автомобиль изобретён, то в патенте количества автомобилей нет всё равно, но есть информация, что автомобили теперь есть. Просто есть. Как понятие. Без указания количества. Не значимость — это вообще третье. Вот есть у тебя термометр. А у него какие то показания. От чего они зависят? От температуры воздуха. А ещё? Как ни странно, от атмосферного давления: под действием атмосферного давления и резервуар с подкрашенным спиртом, и капилляр, по которому он течёт мимо шкалы, сжимаются, а объём спирта остаётся прежним, высота столба увеличивается. На сколько? На незаметную величину. И изменения показаний термометра под действием меняющегося атмосферного давления полностью маскируются изменениями показаний того же термометра под действием меняющейся температуре воздуха. Вот атмосферное давление и не значимо для показаний термометра. Оно не ноль, а как раз огромно. На одну и ту же поверхность атмосферное давление действует с силой, эквивалентной весу полуторатонной гири, а температура воздуха — с силой, меньшей веса граммовой гири. Но температура значима, а давление — нет.
Ответить
-
-
Нет. Именно это я и оспариваю. Сброшенный флаг обозначает отсутствие чего либо как категории. Ноль означает только фактическое отсутствие объектов, к этой самой категории относящихся, и требует для своего существования существования и категории. Пока автомобиль не изобретён, сброшен именно флаг существования автомобилей, при наличии патента на автомобиль он существует как понятие, но в конкретном гараже может не стоять ни одного автомобиля. Это разные классы отсутствия: пока автомобиль не изобретён, за вопрос об их количестве можно вообще в психушку угодить, а то и на костёр, если церковь зверствует, а когда категория существует, можно уже спрашивать вполне безопасно даже о фактически пустом гараже. Значимость — это вообще другое. Значимость — это когда количество важно, а не значимость — это на количество плевать. Атмосфера, у самого её бак с жидким гелием, у дна пластина, в ней в виде резервуара и канала жидкостного термометра, в ней жидкий гелий и некоторое количество паров гелия, площадь пластины два квадратных метра. С какой силой на неё давят гидростатиченское и атмосферное давления? Весом нескольких десятков тонн. А с какой силой по той же пластине бьют молекулы за счёт только теплового движения при температуре 3 Кельвина? Много меньше. Но эти удары значимы, а давление нет. Почитай сначала теорию регрессионного анализа, а потом пиши, что такое значимость и как она соотносится с существованием. Самого количества может не быть, только если чего то нет как категории. Но тогда вопрос о значимости вообще не стоит.
Ответить
-
-
«Категория — это всего лишь обобщающая систематизация (перечень, каталог), того, что есть.» Оно конечно так. Но вот придумал некто фотонный звездолёт, а звездолёта не построил. Это тоже обобщающая категория, в которую войдут корабли разных классов с разным отношением массы топлива к массе корабля и, соответственно, разной скоростью. Одни корабли достигнут десятой части скорости света, другие — половины, третьи на десятую отстанут. Одни корабли одноместны, другие возят сотни тысяч колонистов, третьи — вообще беспилотные зонды. У них и само топливо разное. На одних это протоны и антипротоны, на других — свинец и антисвинец. Категория есть, она обобщает, а самих объектов в ней нет. И даже в фантастических книгах всё это разнообразие появилось позже, а сначала был сам принцип аннигиляции чего то с чем то для получения излучения, масса которого будет достаточна для разгона корабля. То есть признак, по которому весь этот «зоопарк» снесён в одну категорию, придуман заранее, до того, как в ней появились даже конкретные образы кораблей. А спросите того фантаста, сколько таких кораблей на реальной Земле. Он скажет, что их нет и быть не может. Вот это и есть ноль. Но вопрос то понят и на него получен ответ. А теперь такой вопрос: «Сколько на Земле дерабузоторов?». Теперь не понят даже вопрос. Потому что нет даже такой категории. Ноль не состоит из элементов и добавлять их в него нельзя. Вот есть пустая полка. Раз она пустая, значит предметов на ней ноль. Поставим на неё глобус. Теперь предметов на полке уже не ноль. Число изменилось. Теперь введём множество объектов на полке. Полка пуста? Ну тогда и множество пустое. Поставим на полку глобус. Множество больше не пустое. Но это ТОЖЕ САМОЕ МНОЖЕСТВО. Просто в него добавлен элемент. Полка то у нас осталась той же, а изменилось количество предметов на ней. В чём же разница? Если нас интересует только количество, то полка описывается числом, а пустая полка — нолём. А если нас интересует, стоит ли на полке именно глобус, лежит ли там именно калькулятор и так далее, то полка описывается множеством, а пустая полка — пустым множеством. Именно это отличает множество от числа: каждый элемент множества уникален и может быть задан вопрос о наличии именно его в множестве, число же от конкретных элементов абстрагируется полностью, с точки зрения счётчика змея не отличима не только от черепахи в том же зоопарке, но даже от бомбарды в музее, хотя бомбарда входит в множество экспонатов музея старинного оружия, а змея — в множество животных зоопарка. Эти объекты — элементы разных множеств, но при определении мощности этих множеств учитываются одинаково. И у множества только мощность выражается числом. Пустое множество отвечает на вопрос ЧТО СТОИТ на пустой полке, ноль — на вопрос СКОЛЬКО предметов стоят на пустой кнопке, а сброшенный флаг — на вопрос МОЖЕТ ЛИ БЫТЬ ПОНЯТ САМ ВОПРОС. Это разные вопросы. И ответы на них разнотипны.
Ответить
-
«А сжигать на кострах — это вы умеете. Только правду не сожжёшь!Ё!» Учёные как раз на кострах горели, а не жгли.
Ответить
-
«А раз чего-то нет то нет и его значимости.». Бред. Вот есть у нас вакуум и есть барометр. Что покажет барометр? Ноль. Это значит, что давление не значимо? Нет. Накачайте в шлюз воздух и тот же барометр покажет треть атомосферы. Так как же может быть не значимо для положения стрелки то, что давление только что не было? Ведь барометр показывал ноль ТОЛЬКО ПОТОМУ, что давления не было. Другой пример. Есть барометр и есть прожектор, яркость которого можно регулировать. Прожектор светит на барометр максимально ярко, барометр показывает 16 атмосфер. Значит ли это, что яркость света значима для положения стрелки? Нет. Уменьшите яркость. Да не в жалкие два раза, а пусть теперь прожектор притворится ручным фонариком. Стрелка с места не сдвинется. Потому что яркость в данном случае не значима.
Ответить
-
«Нуль и в пустых разрядах сам по себе не имеет значения. » Бред. Ноль имеет значение, так как отмечает, в каких же на самом деле разрядах стоят остальные цифры. А в другом случае не значащ. Значимость означает, что что то чему то равно ИМЕННО ПОТОМУ, что вот это значимое именно такое. И значимость цифры означает, что число чему то равно ИМЕННО ПОТОМУ, что цифра именно такая. То есть если величина значима, то её изменение означает изменение другой величины и если цифра значаща, то её изменение означает изменение самого числа. Вне контекста изменения нет ни понятия значимости, ни понятия значимости цифры. Кстати, обратите внимание на различие в прилагательных: значимая величина, но значащая цифра и ни когда наоборот.
Ответить
-
-
-
-
-
-
-
-
Ноль не обозначает отсутствие цифр, он сам — цифра. Но не только. Ноль — это ещё и число.
Ответить
-
-
Нет. Просто «значимость» и «значимость цифры» — совершенно разные термины. Вы же, когда в такси садитесь, не говорите вместо «Улица Кирова 73»: «ли рова се ри»? Вот и здесь не глотайте слова. Кроме того, не путайте значение числа и знаки, которыми оно записано. Ноль бывает не значим только в ипостаси цифры, ещё бывает не значима сама величина при любом значении. Но вне ЗАПИСИ числа не может быть не значим только ноль.
Ответить
-
-
Конечно понимаю. А что здесь можно не понять? Кстати, переменная бывает значимой, а цифра — значащаей, ни как не наоборот.
Ответить
-
-
-
Да и цифра 0 бывает значима. 232 и 00232 — одно и то де число, но 232, 20032, 23002, 23200, 20302, 20320 и 23020 — разные числа. А различаются только нолями. И даже ноль слева бывает значим: 0,2 и 0,002 — разные числа. А справа бывает не значим: 0,200 и 0,2 — одно и то же число.
Ответить
-
-
Разрядом как и раз называется место цифры в числе. То есть, если в твоём бреде упростить лексику то получится: «Значимость места цифры в числе имеет не ноль, а самом место места цифры в числе в числе», что не возможно даже распарсить. Соответственно смысла здесь нет.
Ответить
-
-
-
-
-
я думаю что этот вопрос мы сами себе придумали)) теперь и мучаемся . 0 это что ? это пустота! и мы пытаемся узнать о пустоте.. ноль это ничто.. я считаю что есть только сложение .. а умножение это просто что бы не писать 5+5+5+5 а мы просто пишем 5*4 … мне кажеться это самое большое заблуждение что умножать вообщще можно , можно только прибавлять . а вот за это упрощение и и получили такой парадокс х/0= ? а может его и нет)) если с моей точки зрение он ничего не играет роли..если убрать нах умножение то и пропадет деление.. и останеться отнимание и прибавление
Ксати это и не так уж и детский вопрос..
З,Ы я подхоил с точки образного мышления)
Ответить
-
Попробуйте через сложение выразить pi*exp(1). Функция exp — это экспонента, то есть степень основания натурального логарифма. Или попробуйте через сложение не аргументов, а самих логарифмов выразить ln(2)*ln(10).
Ответить
-
-
Не понимаешь как раз ты.
Ответить
-
-
«А вот (х*0=0) для реактора катастрофа.» Нет. Катастрофа будет, если x*1=0 получится ВМЕСТО x*1=100. А если не вместо, да ещё и х*0=0, то это всего лишь означает, что реактор «заглох» и сколько стержни не дёргай, он от этого не «заведётся». Если же х*0=0, но вместо другого уравнения, то это катастрофа, но с некоторой вероятностью. В этом случае он может:
1. «Заглохнуть».
2. Взорваться.
3. Продолжить функционирование в прежнем режиме.
4. Увеличить мощность в допустимых пределах.
5. Уменьшить мощность без прекращения цепной реакции и подачи пара на турбины.
Целых пять вариантов, катастрофичен из них только один, причём, далеко не самый вероятный.
Если же при счёте овец получится x*0=0, то чабан УЖЕ ОСЛЕП.Ответить
-
«Да, господин «учёный», математика одна, но только если она правильно отражает физику. Поэтому постарайтесь понять, что если умножать на 0, т.е. ни на что не умножать, то это значит оставить всё как есть.» Нет. Оставить всё как есть — это умножение на 1.
Ответить
-
» Ведь прибавить ничто, в результате чего с реально существующим операндом ничего не происходит — это физически равнозначно умножению его ни на что. Не так ли?» Нет. В реакторе 100 стержней. Если к ним прибавить 5, то добавится всего 5 стержней, а если их на 5 умножить, то добавятся целых 400 стержней. Ноль ведёт себя также: если к имеющимся стержням прибавить 0 стержней, то их так и будет 100, а если их на 0 умножить, то поднимутся даже те 100, которые были. Разумеется, исчезнуть они не могут. Но они могут быть не сделаны, если умножить на этапе проектирования. И тогда стержней не будет вообще. У астрономов есть шутка о том, что чёрные дыры появились там, где на 0 поделил бог. Вообще разность множителя и произведения зависит от обоих множителей. И ещё. Чему равно 20*6? Это 2*10*6+0*1*6. 2*10*6=120, 0*1*6=6(по-твоему). Итого 126. 21*6=2*10*6+1*1*6. Возьми по 6 один раз. Сколько будет? 6. Возьми по столько один раз. Сколько будет? Опять 6. Итого 126. Получается, что 0 и 1 — два глифа одной цифры. А теперь возьми 6 раз по 20. Сколько получилось? 120. 126 не получается ни как.
Ответить
-
-
-
» А для того, чтобы вернуться к физике, т.е. к действительности рекомендую вам ознакомиться двумя материалами: http://alaa.ucoz.ru/publ/fizika_i_matematika/moi_stati/fizicheskie_oshibki_arifmeticheskikh_operacij_operacii_s_nuljom/2-1-0-51 и http://alaa.ucoz.ru/publ/fizika_i_matematika/moi_stati/fizicheskie_oshibki_differencirovanija_chast_i/2-1-0-45.» Не случайно на укозе. Жёлтая «пресса» называется жёлтой по цвету бумаги, так как этим «газетам» не хватает денег на покупку более дорогой белой бумаги из-за того, что они не интересны ни одному серьёзному человеку, а шпаны нет денег на покупку дорогих изданий. Укоз же даже до неё не «дорос». Математика одна и та же, хоть ты стержни в активной зоне реактора считай, хоть овец. Ни каких таких физических основ она не имеет. Физическим бывает смысл отдельных математических понятий. Например, производная — это скорость. А в других случаях это расход жидкости. Или электрический ток. Или вообще артангенс уклона горы. А вторая производная — это ускорение. Или кривизна горного склона. Или скорость изменения электрического тока. Или скорость изменения расхода жидкости. И ошибки в операциях с числами, соответственно бывают только математическими. Физические ошибки бывают в выборе модели, а значит и самих операций.
Ответить
-
-
-
За операцией и»тоже сложение стоит? А за или? За исключающим или? За сдвигом? За сравнением? За переходом по адресу? Сложение вообще не обязательно реализовывать аппаратно, его отлично можно заменить логическими операциями. А наоборот не получится. А умножение обязательно, но только на основание внутреннего представления. Потому что сдвиг нельзя представить через какие бы то ни было другие операции.
Ответить
-
-
Я и не путаю. В отличие от некоторых. Аппаратной бывает реализация. Но не процессы, этой реализацией заданные. А процессы как раз физические. И если я по привычке лихо проскочил уровень «за единицу принято 5 Вольт», это ещё не значит, что за переносом из комбинации сдвига и операции and стоит магия.
Ответить
-
-
-
-
А инженеры уже давно сделали прибор, при помощи которого можно делить и умножать на ноль. Каждый из нас таким прибором регулярно пользуется по нескольку раз на день :)))http://www.webstaratel.ru/2012/01/delenie-na-nol-v-fizike.html
Ответить
Основы логики: 0→0=1 (Из нуля следует ноль. Значит это может быть равно чему угодно, т.е 1)
Ответить
«Компутер — он ить не только «складывает» — он еще и СДВИГАЕТ»
Быть может зная больше о программирование на низших языках, вы бы знали что действительно все основные математические операции представлены через сложение, есть даже формулы выражения всех операций через сложение. Достаточно почитать учебник высшей математики 1 курса, там это всё есть.
«То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5»
Нет. Также читайте учебники — вычитание это сложение с отрицательным числом, т.е. 5 — 3, это 5 + (-3), опять же в школе рассказывают в начальных классах, только мы не обращаем внимания. Да и ещё вы переносили цифры, составляли уравнение, вводили какую-то переменную «x» (которой кстати нет в первоначальной записи 5 — 3) — это лишние действия.
«То есть это задание найти такое число, которое при умножении на 0 даст 5»
«Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует»
Быть может, вы имели ввиду целое число, так как я знаю — это дробь (5/0), ведь и правда (5/0) * 0 = 5.
«Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому.»
В первую очередь вам скажут забудьте всё что учили в школе. И затем расскажут как и с 0 обходится и что корень из 2 это рациональное число и прочие изыски. Автору полезно было бы ознакомится хотя бы с началами мат. анализа, прежде чем такие статьи писать.
Ответить
-
Бред. Во-первых НЕ БЫВАЕТ низших и высших языков. Есть языки разных уровней и парадигм, но уровни не превосходны. Например, язык ассемблера — язык низкого уровня. Низкого, а не низшего. Тем более не низший. А во-вторых все операции реализуются через and, or, xor и сдвиг. Сдвиг — это умножение в чистом виде, а сложение как раз реализовано через or, xor и and.
Ответить
-
-
Бред как раз у тебя.
Ответить
-
-
Например, в твоём утверждении, что утверждение: «Состоявшийся учёный давно знает физический смысл математических понятий и операций» является бредом. В твоих россказнях о высших и низших языках. В твоём утверждении о том, что все операции представлены сложением. На самом деле битовые операции, логические операции, операция перехода на адрес и операции доступа к памяти НЕ МОГУТ быть реализованы с помощью сложения. Наоборот, арифметические операции реализуются через битовые и логические, а переход на адрес и доступ к памяти вообще НЕ МОГУТ БЫТЬ СВЯЗАНЫ С ДРУГИМИ АППАРАТНО РЕАЛИЗОВАННЫМИ ОПЕРАЦИЯМИ кроме однотипных. Если составная операция реализована программно или даже микропрограммно, пожалуйста, нет ничего проще. А если другая операция реализована аппаратно, то она ни как не может быть связана с переходом на адрес и доступом к памяти. Вызов подпрограммы и возврат из подпрограммы — это тоже переход на адрес, но одновременно и тоже доступ к памяти, операции, используемые для организации циклов (кроме сравнения), — тоже доступ к памяти, стек — часть памяти, операции, подобные MOVS, — тоже доступ к памяти, а обработчик прерывания — тоже подпрограмм. Таким образом, реализация вызова подпрограммы с помощью перехода на адрес и доступа к памяти — пример реализации составной операции, однотипной и с переходом на адрес, и с доступом к памяти, контрпримером не являющийся.
Ответить
-
-
-
-
Люди, у меня такое мнение на этот вопрос. Математика описывает жизненные ситуации, помогает людям решать реальные задачи. Все операции, определения и т д нужны для реальных задач. Даже мнимые числа имеют применение. А вот деление на нуль не пригодится ни в одной(!) жизненной ситуации. По-этому деление на ноль не имеет смысла.
Ответить
-
NekoNeko
Артем12345
06.08.2013
15:30
Ответить
>Математика описывает жизненные ситуации, помогает людям решать реальные задачи. Все операции, определения и т д нужны для реальных задач.
Нет.
>Даже мнимые числа имеют применение.
Да.
>А вот деление на нуль не пригодится ни в одной(!) жизненной ситуации.
Нет.
>По-этому деление на ноль не имеет смысла.
Нет.Ответить
-
taras
Артем12345
11.10.2017
19:19
Ответить
Ну так не имеет, что на дроби 0/0 построена четверть теории пределов и всё дифференциальное исчисление.
Ответить
-
-
Не только уже, но и давно. В отличие от некоторых.
Ответить
-
-
Бред как раз несёшь ты.
Ответить
-
-
-
-
-
Дифференцирование — это поиск производной. А производная есть предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нолю. Но ведь в этом случае приращение гладкой непрерывной функции тоже стремится к нолю. И получается, что всё дифференциальное исчисление — это поиск значения именно дроби 0/0. Пределы бывают чего угодно. В том числе, отношения двух величин. В том числе, стремящихся к нолю. И опять получается дробь 0/0. Просто пределы этой дробью не исчерпываются.
Ответить
-
-
Нет. Речь именно о смысле ЗАПИСИ 0/0. К ОПЕРАЦИИ деления она ни какого отношения НЕ ИМЕЕТ. Если тебе от этого будет легче, то считай, что любой толковый математик владеет хитростью, позволяющей делить на ноль, не деля на ноль. Бредово выглядит. Но ничего лучше ни из производной, ни из правила Лопиталя не выжмешь.
Ответить
-
-
-
Не зная даже что такое ноль, берёшься оценивать мою диссертацию и даже науку в целом. Капец.
Ответить
-
-
-
Кто может объяснить, почему когда я 5 делю на 0,000000000000001 калькулятор с ошибкой выдает число 1,004504505255465 ? то, что ошибка — понятно — все число не влезло, но если потом его умножить на 0,00…01 то получится только это самое 0,00…01, даже близко к 5 нет. НО такого правила нет, что на 0,00…01 нельзя делить, значит все-равно должно после деления более-менее разумно число получаться, которое если умножить на делитель, должно результировать примерно то же самое делимое, что было в начале (5). ПРостите за такой язык, я не математик, просто интересно стало.
Ответить
-
Ди Ради
landlawyer
06.08.2014
03:47
Ответить
Не влезает в разряд.
Будет 5 и куча нулей.
Но калькулятор вычисляет по-другому. Из-за архитектуры микрухи.Делить 5 на 0,000…001 это тоже самое, что умножить 5 на 10000…0000, т.е. будет в итоге 50000…000000000
По основному вопросу статьи:
Ноль не число. Поэтому делить на ноль нельзя, точно так же, как делить на стулья. Ноль это пустое множество, оно не является числом. Числом может являться элемент внутри множества, но не множество.Т.е. пытаться разделить 37 на 0, это тоже самое, что пытаться разделить 37 на акведук или римского императора Нерона, ну или на зубную щетку.
Т.е. вся проблема вопроса в определениях, которыми оперируют те, кто не изучал deep матан.
Если вы поймете, что ноль не является числом, то вы поймете почему нельзя проводить составные операции с нулем в поле чисел.Ну т.е. мы тогда, грубо говоря, пытаемся разделить пчел на киев, огород и бузину.
Ответить
-
taras
landlawyer
11.10.2017
19:20
Ответить
Он бракованный. Должен сообщить о переполнении явно и отказаться выполнять над результатом дальнейшие операции.
Ответить
Ну во первых, при сложении (умножении, вычитании, делении) на ноль второе число должно быть — не ноль, потому что в таких примерах теряется всякое представление о несущей, в этом примере информации, т.е. информация должна составляться минимум из двух разных единиц (например двоичный код), из которой впоследствии можно составить более сложную информацию. Так что такие примеры как 0+0=0, 0-0=0, 0*0=0, 0/0=0 существовать не могут в принципе. Что же касается ДУРИ, которая описана в этой статье, могу сказать, что если ученые не нашли способ при котором деление на ноль не приводит к какому-то определенному результату, то они могли бы обратить внимание, хотя-бы, на массу логических (системных) противоречий содержащихся в этой статье.
Ответить
-
Не слушайте детишки. Эти альтернативщики вам заморочат голову.
Официальный матан позволяет операции 0+0, 0-0, 0*0, 0/0.
Пустое множество плюс пустое множество = пустое множество.
То же самое с минусом и умножением.А вот с делением выйдет неопределенность, которую дальше можно раскрыть по законам теорвера.
А вот числа нельзя делить на ноль, не потому что нельзя, а потому что ноль не является числом.
То же самое как 32 нельзя разделить на банановую кожуру. Потому что банановая кожура не является числом.Ответить
-
Тогда почему умножать на ноль можно??? По Вашему такое уравнение: «32 * банановую кожуру» более осмыслена чем «32 / банановую кожуру?»
Ответить
-
Потому что 0 это пустое множество.
Если умножить что-то на пустое множество, то мы получим это что-то в пустом множестве, т.е. нету места там для числа. Оно пустое, содержит нисколько элементов. Поэтому если умножить на пустое множество банановую кожуру то и получим пустое множество.Вся непонятка из-за того что в школах не объясняют что такое «арабские» (индоарабские) цифры вообще. Т.е. наши современные (Еще в средние века европейцы пользовались римскими цифрами).
Так вот, наши цифры — комплексны. Т.е. имеют сложность от позиции.
Например в числе 38448 — первая восьмерка означает 8000, а последняя просто 8. А выглядят они одинаково. Просто меняется положение и порядок цифр.Так вот 0, когда он находится за другими числами или перед — например 100, 550, 20, 0,005, 0,1 — является Цифрой.
А когда он без чисел ни слева ни справа то он не является числом вообще. А обозначает пустое множество.Если пустое множество разделить на пустое множество — будет неопределенность. Т.е. 0/0 = неопределенность.
А умножая на ноль мы помещаем число которое умножаем в пустое множество (множество без элементов) и места числу не остается. В итоге на выходе мы получаем пустое множество. Вот почему 5*0 = 0.А что будет если мы разделим 5/0? А ничего не будет, т.к. в данном случае мы делим число на пустое множество без элементов. Данная операция означает «сколько в 5 содержится пустых множеств?» — бесконечное количество. Вот такой ответ.
Сам ноль был изобретен Индусами (и как цифра и как пустое множество) и конкретно благодаря ему стали возможны уравнения.
Ответить
-
Хорошо. 5+5+5+5+5+0=25 ; 5+5+5+5+5*0=20 все сходится! Просто при умножении на пустое множество число растворяется в пучине бездны, уходит в некуда, наплевав на закон сохранения энергии. А вот если прибавить пустое множество, то закон сохранения энергии сохраняется, и числа в таком пустом множестве чувствуют себя вполне нормально. 5*5*0=0 наперстники нервно курят в сторонке.
Ответить
-
В смысле «уходит в некуда». Ну некуда. Кстати, положить? Или, может, налить? Но в любом случае с предлогом «в» оно уже не сочетается.
Ответить
-
-
VladNSK
Ди Ради
31.10.2016
04:10
Ответить
Ди Ради написал: «Потому что 0 это пустое множество.
Ноль — такое же число, как, например, 1 или -5.23. Чтобы это понять — достаточно поглядеть на термометр за окном: там на шкале есть положительные числа, ноль и отрицательные.
Утверждать, что «ноль — не число, а пустое множество» — столь же глупо, как и утверждать, что не бывает нулевой температуры.
Ответить
-
Бред. Ноль — это вообще не множество. Это число. А пустое множество — не ноль. Также как и нуль-вектор или нуль-матрица. А 0i, 0+0i, нулевой кватернион и нулевой октанион — это всё тот же ноль. То есть ноль — это особое число не одного, а шести разных типов.
Ответить
-
-
А что же это? Синий Пикачу?
Ответить
-
-
Нет. Я как раз знаю, что ноль — это число.
Ответить
-
-
-
-
-
И НЕ ВОЗМОЖНО получить «это что то в пустом множестве», так как множество, в котором есть «это что то» уже не пусто.
Ответить
-
-
Не переживай. Скоро в школу, там объяснят.
Ответить
-
-
В отличие от некоторых нет. У тебя знания трёхлетнего малыша.
Ответить
-
-
-
-
-
-
-
Не переживай. Скоро в школу, там объяснят.
Ответить
-
0 — тоже число. И матан не разрешает ОПЕРАЦИЮ 0/0, вычисление же предела — это нифига не деление.
Ответить
-
-
Во-первых сам предел — это вообще не операция. Во-вторых не бывает деления в пределе. Бывает предел отношения. И ищется он безо всякого деления. Например, предел (f(x2)-f(x1))/(x2-x1) при x2-x1, стремящемся к нолю, ищется по двум таблицам, в одной перечислены производные простых функций, а в других — правила вроде f1`(f2`(x))=f1`(x)*f2`(x), или «производная суммы равна сумме производных». Делить приходится ровно в двух случаях: при применении правила Лопиталя и когда дифференцируемая функция сама содержит дробь. В обоих случаях делителем бывает что угодно кроме ноля.
Ответить
-
-
-
-
Задумывался. Но пустое множество — не ноль, а множество. Также, как нуль-вектор — это вектор, а нуль-матрица — это матрица. Нуль-вектор даже не единственен, он бывает разных размерностей. А нуль-матрица может иметь разное количество и столбцов, и строк. Ноль же — это разве что МОЩНОСТЬ пустого множества. Но не само множество. В программировании, кстати, в множество, даже в пустое, можно добавлять элементы (после этого оно точно не будет пустым). А в ноль элементы добавлять нельзя. Это ли не пример того, что ноль и множество — величины РАЗНЫХ ТИПОВ? «аз уж вы такой сторонник слова «нельзя» в точной науке математике, то вам не кажется, что пустоту нельзя называть множеством, » Пустоту как раз можно. В ОТЛИЧИЕ ОТ НОЛЯ. Ноль — это количество. Например, количество элементов пустоты. С точки зрения моей прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабки пустой мешок и ноль (если ей объяснить, что такое ноль) — одно и то же. Но для меня пустой мешок — это только контейнер, описываемый нолём. И только в случае, когда каждый отдельный предмет в мешке не имеет индивидуального значения. А если имеет, то мешок описывается множеством и ноль к нему уже относится косвенно, даже если он пустой.
Ответить
-
-
Ты их видел вообще? Мой научный руководитель — дважды член-корреспондент академии наук. Так вот, подзаборная алкашня сложней изъясняется. А за непонятными словами прячут отсутствие предмета разговора «экстрасенсы» да попы. И это и есть простое объяснение. То есть объяснение проще, чем на пальцах.
Ответить
-
-
-
-
-
НЕ БЫВАЕТ несущей информации. Несущими бывают стены, балки, частоты. Но не информация.
Ответить
-
-
Ты хоть знаешь, что такое исходники? Умножать их нельзя. И какое они имеют отношение к несущей?
Ответить
-
-
Вот только ты отвечал именно на утверждение о том, что информация несущей не бывает. Так кто бредит? И какое отношение исходные условия имеют к исходникам?
Ответить
-
-
-
-
-
«теряется всякое представление о несущей, в этом примере информации, т.е. информация должна составляться минимум из двух разных единиц (например двоичный код), из которой впоследствии можно составить более сложную информацию. Так что такие примеры как 0+0=0, 0-0=0, 0*0=0, 0/0=0 существовать не могут в принципе.» Не путай систему кодирования и отдельно взятое утверждение.
Ответить
-
-
Я как раз не путаю. В отличие от некоторых. Деление — операция как раз математическая, а не физическая, а математика целиком состоит из искусственных сущностей, к тому же ещё и идеальных. И лишь описывает физику, но физикой не является.
Ответить
-
-
Бред. Математика может говорить что угодно. Вопрос о соответствии физической действительности решается только экспериментально. Например, математика может говорить и о том, что F=-G*m*M*r/(|r|^4), или что F=-G*m*M*r/(|r|^3), а физика говорит только что F=-G*m*M*r/(|r|^3). И не надо рассказывать, что сила притяжения обратно пропорциональна квадрату расстояния, отношение вектора к кубу его модуля именно квадрату модуля и обратно пропорционально, но, в отличие просто от дроби с квадратом скаляра в знаменателе, имеет направление. Конкретный же показатель может быть определён только экспериментально, математически его не выведешь. Можно конечно из зависимости гравитационного потенциала от расстояния. Вот только она сама по умолчанию тоже не известна и может быть выведена только из самого закона всемирного тяготения. К тому же математика — язык не только физики, но и химии и даже информатики. А там свои законы, с физическими связанные разве что как следствие с причиной, да и то не все.
Ответить
-
-
-
-
Мне кажется, что в природе частица (атом или ещё что-то) либо есть, либо частицы нет – абсолютный ноль как отсутствие. Другого ноля в природе нет.
Математика – произведение рук человеческих, модель природы для облегчения жизни человека. Ноль в математике не значит «отсутствие», как в природе. Это недоработка математиков, неточность модели. На этом дефекте модель (математику) заклинивает.
Я уже много лет веду всевозможные расчёты для практических целей (сметы, режимная наладка, тепловые и прочностные расчёты и прочее) и сделал себе пользовательскую функцию, типа: «если делитель=0, то принять результат за 0».
Много лет считаю, ставлю при отсутствии данных ноль, и все расчёты проскакивают на «ура».
Для практических расчётов этот метод очень даже годится.
Ответить
-
Полностью согласен, нынешняя модель математики далека от совершенство. Уже на данном этапе развития человечества, с помощью действующей десятеричной модели исчисления не возможно вычислить правильный ответ на вполне физическое явление. К примеру, давайте вычислим за какое время спортсмен обгонит черепаху, если нам известно что спортсмен бежит со скоростью 10 км/час, черепаха со скоростью 1 км/час, и спортсмен дает фору черепахе в 10 км. Ответ будет следующий: через 1,1111….до бесконечности часов., то есть никогда, но физический это произойдет. Как можно записать правильный ответ?
х*0=0; у*0=0
следовательно х=у, но по факту х=5 а у=7. По моему противоречий нет, иначе умножение на ноль тоже бы запретили.Ответить
-
Судя по вашим комментариям, Вы сами весьма далеки от математики
ответ 1.11111… говорит лишь о том, что момент этот произойдет спустя 1 час 6 минут и 6 секунд с небольшим (далее идет лишь определение погрешности с точностью до какого разряда будет выполнен расчет)
но это не говорит нам о том, что этого не произойдет никогда вовсе
А поскольку изначально вопрос ставился о том, через сколько мы сможем зафиксировать непосредственно факт обгона, то ответ с точностью до секунды будет выглядеть как 1 час 6 минут и 7 секунд.
И не надо тут выдумывать ничего лишнего.Ответить
-
«1 час 6 минут и 7 секунд» — ответ неверный. «спустя 1 час 6 минут и 6 секунд с небольшим» — примерно так производят расчеты при отправке ракет в космос.
Ответить
-
-
Не переживай, скоро научишься.
Ответить
-
-
Не путай число с флагом. Есть/нет — это флаг. А ноль — это число. И он относится не к частице, а к энергии, времени, пространству. К непрерывным сущностям, которых может быть разное количество.
Ответить
1. Полностью согласен с «?ё!». как можно умножая на ничто получить ничто, если умножение — это многократное сложение? 5+0+0 = 5
2. Ошибка в том, что ученые «признаю полноценными только [+] и [*]
Отрицая существование [-] и [:] отрицается закон сохранения энергии.
5-3 = 2 Тройка в данном случае не исчезает, а трансформируется в то, что уже не учитывается в рамках данного выражения. В противном случае [х+2=5]иногда не ровнялось бы [3]
PS: аксиомы — способ обмана человечества
Ответить
У меня такое впечатление, что для математиков не проблема поделить на 0, а физики давно и успешно делят). Правда, для этого приходится придумывать разные обходные пути. А это как я поделил:
https://youtu.be/_U1WP1s2EUI
Ответить
-
Вся проблема в том, что когда в качестве доказательства какой либо теории используется ошибочный аргумент (заведомо неправильный эксперимент), то и результат будет соответственный (неверный).
В Вашем примере в частности, и во всех в целом, в качестве главного аргумента в пользу запрета деления на ноль является тот факт что: «Любое число умноженное на ноль дает ноль». Но это-же неверно!
Эту проблему можно решить другим путем. Можно разрешить деление на ноль, а умножение запретить, тогда получим что 5/0=0 ; 4/0=0, следовательно 0*0=(любое число) и 5*0=(умножение на ноль запрещено), следовательно умножение на ноль запрещаем, так как это ведет к противоречиям.
То-есть у нас получается, что мы запрещаем одну операцию потому что она противоречит другой операции, хотя они обе являются неправильными.
Умножение на ноль, так-же как и деление, говорит только об одном, что никакой операции не происходит. То-есть, либо в результате обеих операциях нужно выдавать ошибку, либо результат должен быть аналогичен с результатом деления или умножением на единицу.
И потом, более логично представить что при деление целого можно прийти к нулю, нежели при умножении…
Ответить
Короче, ноль это дверь в хаос. Эту дверь открывать нельзя. Поэтому и на ноль делить нельзя
Ответить
«Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. » Ну так не имеет, что на этой дроби даже определение производной построено. Более того, дробь 0/0 — важная часть ВСЕЙ теории пределов.
Ответить
-
-
Это я то? А ничего, что я написал и защитил диссертацию по специальности 05.13.18? И где ты умудрился откопать сомнения? Тем более какие то мифические категории бреда.
Ответить
-
-
Образованные люди знают, сколько в русском языке местоимений.
Ответить
-
Покажи хоть одно моё безапелляционное заявление.
Ответить
-
И где у меня хоть одна претензия на хоть какое то понимание всего?
Ответить
-
«В науке, как и во всех сферах человеческой деятельности, полно не только гениев и порядочных людей, но и всяких бездарей, которые занимаются плагиатом и прочими спекуляциями от науки.» Тебя не полно, не ври.
Ответить
-
«Если вы настоящий учёный, то дайте, пожалуйста ссылки на ваши работы и научные достижения. Возможно я изменю мнение о вашем понимании в науке.» Ол комплит. http://www.dissercat.com/content/matematicheskoe-modelirovanie-v-zadachakh-optimizatsii-elektroshlakovogo-protsessa-i-vnepech
Ответить
-
-
-
-
!Ё!, вы пишете ерунду, не имеющую никакого отношения ни к математике, ни к физике.
Ответить
Сложение и вычитание не только не стоят за остальными операциями, но даже больше того. Это ЕДИНСТВЕННЫЕ операции, которые ВСЕГДА приходится реализовывать через другие. А именно как комбинации or, xor и умножения на основание. И умножение только в младшей школе реализуется через многократное сложение одного из множителей, да ещё на некоторых арифмометрах. В остальных случаях умножение не на основание реализуется через сложение промежуточных произведений, умножение на основание и умножения одного множителя на цифру другого. В двоичной системе через сложение промежуточных произведений, умножение на основание и and. Обязательными же операциями являются: копирование данных из памяти в регистр, копирование данных из регистра в память, умножение на степень основания, сравнение, or, and, xor и переход. Только эти операции во-первых необходимы, а во-вторых действительно элементарны. Ну для перехода к следующей операции ещё приходится реализовывать инкремент. Но это та же комбинация or, xor и умножения на основание, что и сложение. Точнее это сложение с единицей. Так что переход к следующей операции как ни странно элементарным только числится на уровне логической структуры системы команд, а не на уровне физики процессов в АЛУ.
Ответить
Что тут за гении математики сидят? Почему вы тут обсуждаете почему нельзя делить на ноль, а не создаете с физиками машину времени и разрушаете физические законы?
Ответить
А почему бы не говорить школьникам, что делить на ноль нельзя, потому что никто не знает, как это сделать? И добавлять — …тому, кто сумеет – подарят ноутбук с играми. Не исключено, это может подтолкнуть некоторых из них к математическому творчеству.
Ответить
There are reliable criminal justice research writing services that are very popular for students in search of criminal justice paper writing services and criminal justice assignment writing services.
https://researchpapers247.com/criminal-justice-research-writing-services/
Ответить
Делить на ноль можно, главное понимать, что всё это означает. Доказательство — тангенс прямого угла, который равен синусу прямого угла, деленному на косинус прямого угла. Получается единица, деленная на ноль.
Уже очень давно занимаюсь этим вопросом, наконец-то до меня начало доходить. Чтобы ввести в математику результат деления на ноль, многие стереотипы нужно пересмотреть. И начинать нужно с того, что ноль не является числом. Уже одно это утверждение может вызвать бурю в тихом болоте математики.
Ответить
-
Ага, плюс один на градуснике за окном — это число. Минус один на градуснике за окном — это тоже число, а ноль на том же самом градуснике — это уже не число, то есть нет такой темепературы?
Ответить
На самом деле, всё просто: n/0=n*∞,
где n — любое число.
Ответить
-
∞
Нет такого числа: ни в школьной арифметике, ни в матанализе.
Ответить
Давайте внесем немного лирики в строгий строй арифметики.
Когда-то в детстве, глядя на звезды в ночное небо, этот черный, бесконечной глубины космос, украшенный мириадами звезд, я задавал себе вопрос, который, как сейчас догадываюсь, не может иметь единственного и точного решения: Каким образом из ничего может образоваться нечто материальное и весь наш Мир?
Чтобы не зациклиться и не расплавиться, мой детский разум, выдал тогда такое решение: пустота каким-то образом взаимодействует с другой пустотой, образуя нечто первичное материальное. И тогда понимал всю натянутость совы на глобус этого решения, но пришлось удовлетвориться тем что есть.
А вообще, если не запрещать деление на ноль, то n*0=0 <=> n=0/0
Ответить
Пишу свой проект в учебных целях для работы с обыкновенными дробями.
#include <iostream>
#include "simple_math.h"
using namespace std;
using namespace simple_math;
int main()
{
cout << fraction(1, 2) + fraction(1, 3); // в результате выводит "5 / 6"
return 0;
}
Что если знаменатель какой-то дроби будет равен нулю. Понятно, что нужно выкинуть ошибку, но как это сделать?
if(b == 0)
{
// ОШИБКА!
}
Harry
210k15 золотых знаков114 серебряных знаков224 бронзовых знака
задан 30 июл 2017 в 5:07
Andrey VarfolomeevAndrey Varfolomeev
1731 золотой знак2 серебряных знака14 бронзовых знаков
Если вы хотите работать по C++’ному, то нужно генерировать исключение. Можно собственного типа, можно наследовать от стандартного exception — это уже вопрос стиля и предпочтений. Примерно так —
class DivideByZero {};
...
if (b == 0) throw DivideByZero();
...
try {
cout << fraction(1, 2) + fraction(1, 3); // в результате выводит "5 / 6"
} catch(DivideByZero&)
{
cerr << "Divide by zero error!n"
}
Или, если воспользоваться стандартным — думаю, тут правильнее invalid_argument — то
if (b == 0) throw invalid_argument("Divide by zero error in fraction!");
...
try {
cout << fraction(1, 2) + fraction(1, 3); // в результате выводит "5 / 6"
} catch(exception&e)
{
cerr << e.what() << endl;
}
ответ дан 30 июл 2017 в 6:17
HarryHarry
210k15 золотых знаков114 серебряных знаков224 бронзовых знака
0
Если вас волнует производительность — учтите, что процессор сам умеет швырять такие исключения при делении на 0, однако, в стандарте C++ такой обработки нет — ее надо сделать:
GCC
#include <signal.h>
#include <memory>
int main() {
std::shared_ptr<void(int)> handler(
signal(SIGFPE, [](int signum) {throw std::logic_error("FPE"); }),
[](__sighandler_t f) { signal(SIGFPE, f); });
int i = 0;
cin >> i; // what if someone enters zero?
try {
i = 5/i;
}
catch (std::logic_error e) {
std::cerr << e.what();
}
}
Visual C++
#include <eh.h>
#include <memory>
int main() {
std::shared_ptr<void(unsigned, EXCEPTION_POINTERS*)> handler(
_set_se_translator([](unsigned u, EXCEPTION_POINTERS* p) {
switch(u) {
case FLT_DIVIDE_BY_ZERO:
throw std::logic_error("Divide by zero");
...
default:
throw std::logic_error("SEH exception");
}
}),
[](_se_translator_function f) { _set_se_translator(f); });
int i = 0;
try {
i = 5 / i;
} catch(std::logic_error e) {
std::cerr << e.what();
}
}
Оригинал на enSO
Почему это лучше сравнения с 0 перед делением?
- это задействует аппаратные возможности платформы по отлову ошибок
- работает быстрее (не надо делать лишних сравнений)
- гарантирует, что вы не забудете где-то сделать проверку
ответ дан 30 июл 2017 в 6:31
5
Скрытие значений и индикаторов ошибок в ячейках
Смотрите также вот такую (её=СУММ(ЕСЛИ(ЕЧИСЛО(C2;G2;K2;O2);(C2;G2;K2;O2);»»)) — при=МИН(ЕСЛИ(ЕЧИСЛО(B1:B6);B1:B6;»»))Значение/формула (выбираем «Если значение вВ кулуарах математиков говорят, ЕСЛИ. на вкладке форматирования или собственные. При работе в
Примечания:, а затем выполнитеЩелкните Мы стараемся как можно . С помощью этойНа вкладкеРассмотрим ситуацию, когда формулы можно не выделять таком варианте выдаетValeria555
Преобразование ошибки в нулевое значение и использование формата для скрытия значения
формула ячейке B2 равно что результат деленияСкрытие нулевых значений вЧисло предпочтения отображать или
Excel Web App
-
следующие действия.
-
Число > Все форматы оперативнее обеспечивать вас функции можно определить,Число в таблице содержат как массив, т.е. ошибку в формуле.: Спасибо!! Вы меня
) =Ч(A1) 0, тогда формула любого числа на -
отчете сводной таблицы. скрывать нулевые значения,
-
повторите копирование иСкрытые значения отображаются толькоИзменение способа отображения ошибок. . актуальными справочными материалами
содержит ли ячейка -
в списке заранее ожидаемые значения
-
не надо нажиматьМихаил С. спасли!!вместо А1 ставите возвращает значение 0.
ноль является «неЩелкните отчет сводной таблицы.Скрытие нулевых значений, возвращенных имеется несколько способов вставку для каждой -
в строке формул В поле
В поле на вашем языке. или возвращает лиЧисловые форматы
ошибок. Они не
-
CTRL+SHIFT+ENTER):: =СУММ(ЕСЛИ(ЕЧИСЛО(C2;G2;K2;O2);(C2;G2;K2;O2);»»))Valeria555 верхнюю ячейку вашего В противные случаи ограниченным». Любая компьютерная
-
На вкладке формулой, с помощью реализации всех этих
-
ячейки из примера. или в ячейке,ФорматТип Эта страница переведена формула ошибку.
-
выберите пункт требуют немедленного исправления,=ЕСЛИ(ЕЧИСЛО(C2);(C2)+ЕСЛИ(ЕЧИСЛО(G2);(G2)+ЕСЛИ(ЕЧИСЛО(K2);(K2)+ЕСЛИ(ЕЧИСЛО(O2);(O2)))))Максим: У меня возникла столбца формула должна возвратить программа, при попыткеПараметры условного форматирования требований.Внимание! Чтобы пример правильно
-
если вы редактируетеустановите флажоквведите выражение
-
автоматически, поэтому ееНД(все форматы) однако требуется улучшить, но она: То есть это еще одна проблема,
-
Справа жмем «формат» результат после операции деления на 0,в группеВыделите ячейку, содержащую нулевоеОтображение и скрытие всех работал, его нужно ее содержимое. ЭтиДля ошибок отображать0;;;@ текст может содержать
Эта функция возвращает. представление результатов. Существует слишком громоздка. Можно я и пробовал, в соседнем массиве =>Шрифт= > черный деления значений в просто возвращает ошибку.Параметры сводной таблицы
Скрытие значений ошибок путем изменения цвета текста на белый
(0) значение. нулевых значений на вставить в ячейку значения не печатаются.. Введите в полеи нажмите кнопку неточности и грамматические в ячейке строкуВ поле
-
несколько способов скрытия ли упростить?
-
а потом хотел есть не только цвет => ОК ячейках B2/C2». В Excel даннаящелкните стрелку рядомНа вкладке листе A1.Чтобы снова отобразить скрытые
значение, которое нужноОК ошибки. Для нас -
«#Н/Д». Синтаксис функции: =Тип значений ошибок и
Михаил С. сделать без «СУММ», ДЕЛ/0, но и -
Только числовые значенияУсложним нашу формулу функцией ошибка отображается значением с командойГлавнаяНажмите
-
Чтобы переключиться между просмотром значения, выделите ячейки, выводить вместо ошибок.. важно, чтобы этаНД()введите индикаторов ошибки в:
-
просто формулой, но просто пустые ячейки, будут окрашиваться черным =ИЛИ(). Добавим еще в ячейке #ДЕЛ/0!.
-
Параметрыв группекнопку Microsoft Office результатов и просмотром а затем нажмите Для отображения ошибок
Отображение тире, #Н/Д или НД вместо значения ошибки
Отображение скрытых значений статья была вам.;;; ячейках.=сумм(C2;G2;K2;O2) ни так, ни при чем при цветом . одного торгового агентаНо при необходимости можнои выберите пунктСтили
, щелкните
формул, возвращающих эти клавиши в виде пустых. полезна. Просим васЩелкните отчет сводной таблицы.
(три точки сФормулы могут возвращать ошибкиили в так не получается вводе функции МИНГость
Скрытие значений ошибок в отчете сводной таблицы
-
с нулевым показателем
обойти возникновения ошибкиПараметрыщелкните стрелку рядом -
Параметры Excel результаты, нажмите клавишиCTRL+1 ячеек удалите изВыделите ячейки со скрытыми уделить пару секундПоявится вкладка запятой) и нажмите по многим причинам.О2 — пишет ошибку.
(как было указано): 0mega, спасибо. Все в продажах. Теперь деления на 0. с кнопкойи выберите категориюCTRL+`или на вкладке поля весь текст. нулевыми значениями.
-
и сообщить, помоглаРабота со сводными таблицами кнопку Например, формула =1/0=если(ечисло(N2*Q11/100);N2*Q11/100;0)
-
Мотя =МИН(ЕСЛИ(ЕЧИСЛО(CO1549:CO1836);CO1549:CO1836;»0″)) выше excel2003 получилось. формулу следует изменить в Excel. ПростоПерейдите на вкладкуУсловное форматированиеДополнительно(знак ударения) илиГлавнаяИзменение способа отображения пустыхВы можете нажать клавиши
-
ли она вам,.ОК возвращает ошибку #ДЕЛ/0!,Максим: #ДЕЛ/0 — результат совсем ничего неlika1 на: следует пропустить операциюРазметка и формати выберите «Правила. на вкладке
-
Скрытие индикаторов ошибок в ячейках
в группе ячеек. CTRL+1 с помощью кнопокExcel 2016 и Excel 2013:. Нажмите кнопку поскольку деление на
: неграмотного деления в
-
выдает, а при: помогите, как скрытьСкопируйте эту формулу во деления если в, а затем выполните выделения ячеек» >В группеФормулыЯчейки
Установите флажокили на вкладке
внизу страницы. Для на вкладкеОК 0 недопустимо. ПредусмотреныМихаил С.,
-
EXCEL. формуле МАКС пишет ошибку деления на все ячейки столбца знаменателе находится число
support.office.com
Отображение и скрытие нулевых значений
следующие действия. «Равно».Показать параметры для следующеговыберитенаведите указатель мышиДля пустых ячеек отображатьГлавная удобства также приводимАнализеще раз. следующие значения ошибок:Спасибо за помощь,При выполнении деления Н/Д ((( ноль «Выполнение»: 0. Решение реализовываетсяИзменение способа отображения ошибок.В левом поле введите листаЗависимости формул > Показать
на элемент. Введите в полещелкнуть ссылку на оригиналв группеЗначение 0 в #ДЕЛ/0!, #Н/Д, #ИМЯ?, но мой вариант в EXCEL следуетФайл прикрепить не
вроде была формулаТеперь независимо где будет
с помощью помещения В поле0выберите лист, после формулыФормат значение, которое нужноФормат > Формат ячеек (на английском языке).Сводная таблица
ячейке исчезнет. Это #ПУСТО!, #ЧИСЛО!, #ССЫЛКА! пока что более
-
использовать тривиальные правила получается, готова выслать еслиошибка… ноль в знаменателе операндов в аргументыФормат.
-
чего выполните одно.и выберите выводить в пустых.Вы можете сами настроитьщелкните стрелку рядом
-
связано с тем, и #ЗНАЧ!. приемлемый,так как есть школьной арифметики. на почту.короче, как спрятать или в числителе
-
функции =ЕСЛИ():установите флажокВ правом поле выберите из указанных нижеСкопировав пример на пустойФормат ячеек ячейках. Чтобы они
-
Для применения числового формата, отображение нулевых значений
с командой что пользовательский форматЧтобы скрыть значения ошибок, разница: переделывать формулуВ EXCEL дляПо возможности помогите #ДЕЛ/0! и заменить формула будет работатьТаким образом формула ExcelДля ошибок отображатьПользовательский формат действий.
-
лист, вы можете. Чтобы применить числовой оставались пустыми, удалите
-
определенного по умолчанию, в ячейке илиПараметры;;; можно преобразовать их, во многих столбцах этого существует функция плииииз ))) на 0
-
так как нужно позволяет нам «делить». Введите в поле
-
.Чтобы отображать в ячейках настроить его так, формат по умолчанию, из поля весь выберите использовать в таблице
и выберите пунктпредписывает скрывать любые
-
например, в число на: =если(ечисло(N2*Q11/100);N2*Q11/100;0) или
-
ЕСЛИ.Vесли =E21/D21-1 (ссылается пользователю. число на 0 значение, которое нужноВ диалоговом окне
-
нулевые значения (0), как вам нужно. в списке текст. Чтобы отображалисьЧисло > Общий набор стандартов форматирования,Параметры
числа в ячейке. 0, а затем
-
один итоговый наМаксим
-
: пустые ячейки не на пустые ячейки)Читайте также: Как убрать без ошибок. При выводить вместо ошибок.Формат ячеек установите флажок1
-
Категория нулевые значения, снимитеи нажмите кнопку
-
которые требуют скрывать. Однако фактическое значение
-
применить условный формат, ЕСЛИ(ЕЧИСЛО+ЕСЛИ(ЕЧИСЛО: влияют на формулу.Микки
-
ошибки в Excel делении любого числа Для отображения ошибокоткройте вкладкуПоказывать нули в ячейках,2
выберите этот флажок.
ОК нулевые значения. Отображать
Excel 2010 и Excel (0) по-прежнему хранится позволяющий скрыть значение.Максим
Мотя,
Вы формулу вводите: =ЕСЛИОШИБКА(E21/D21-1;0) для 2007Данная функция позволяет нам на 0 формула в виде пустыхШрифт которые содержат нулевые3ОбщийК началу страницы. и скрывать нулевые 2007: на вкладке в ячейке.Создание образца ошибки: Всё же подскажите,куда нам научным как формулу массива?
=ЕСЛИ(ЕОШ(E21/D21-1);0;E21/D21-1) расширить возможности первого
-
будет возвращать значение
-
ячеек удалите из. значения4. Чтобы снова отобразитьПотребность отображать нулевые значенияСкрытие нулевых значений, возвращенных значения можно разнымиПараметрыОписанная ниже процедура позволяет
-
Откройте чистый лист или можно ли заставить сотрудникам до школьнойValeria555
-
Useful аргумента с условием 0. То есть поля весь текст.В поле.5 дату и время, (0) на листах формулой способами.в группе
-
отформатировать ячейки с создайте новый. СУММЕСЛИ работать не арифметики: Вы имеете в: =IF(D21<>0,E21/D21-1,»») во функции ЕСЛИ. получим такой результатИзменение способа отображения пустыхЦветЧтобы отображать нулевые значения6 выберите подходящий формат
-
возникает не всегда.
Выделите ячейку, содержащую нулевоеБолее новые версииСводная таблица ошибками таким образом,Введите только с диапазоном,. Вы файл виду, что яМикки Таким образом в
после деления: 10/0=0. ячеек.выберите белый цвет.
-
в виде пустых7 даты и времени Требуют ли стандарты (0) значение. Office 2010 Office 2007 щелкните стрелку рядом
-
чтобы текст в3 но и с открывали-то? Видимо нет. нажимаю ctrl+shift+enter и: А если там ячейке с формулой
-
Установите флажокИспользование формулы для отображения ячеек, снимите флажокA на вкладке форматирования или собственные
-
На вкладкеПотребность отображать нулевые значения с командой них отображался шрифтомв ячейку B1, рядом не последовательныхВ файле организована
-
вся формула становится пусто …или пробел D5 первый аргумент
Для работы корректной функцияДля пустых ячеек отображать нулей в видеПоказывать нули в ячейках,BЧисло предпочтения отображать илиГлавная
-
(0) на листахПараметры белого цвета. В
-
0 ячеек (C2;G2;K2;O2)? таблица шаблонного типа, в фигурные скобочки?Useful функции ЕСЛИ теперь ЕСЛИ требует заполнить
-
. Введите в поле пробелов или тире которые содержат нулевыеДанные.
-
скрывать нулевые значения,щелкните стрелку рядом возникает не всегда.и выберите пункт
результате текст ошибки — в ячейку C1
-
Михаил С. в которой рассчитывается Да, я так: =IF(AND(ISNUMBER(D21),D21<>0),E21/D21-1,»») следует читать так: 3 ее аргумента:
-
значение, которое нужноДля выполнения этой задачи значения10Скрытие нулевых значений, возвращенных имеется несколько способов с кнопкой Требуют ли стандартыПараметры в таких ячейках и формулу: Нет, нельзя. влажность отдельных органов, делаю.Катя1979 «Если значения вЛогическое условие. выводить в пустых используйте функцию ЕСЛИ..10 формулой, с помощью реализации всех этихУсловное форматирование форматирования или собственные. становится невидимым.
=B1/C1Мотя а потом складывается
-
V: /// если =E21/D21-1
-
ячейках B5 илиДействия или значения, которые ячейках. Чтобы ониПримерСкрытие нулевых значений вФормула условного форматирования требований.и выберите «Правила предпочтения отображать илиОткройте вкладкуВыделите диапазон ячеек, содержащих — в ячейку A1.
-
: См. файл. сухое вещество. Однако: Да я об
-
(ссылается на пустые C5 равно ноль, будут выполнены если
-
оставались пустыми, удалитеЧтобы этот пример проще выделенных ячейках сОписание (результат)Выделите ячейку, содержащую нулевое
-
Отображение и скрытие всех выделения ячеек» > скрывать нулевые значения,
Разметка и формат значение ошибки.В ячейке A1
Максим не все органы этом. Кидайте посмотрю ячейки)
тогда условие возвращает
в результате логическое из поля весь было понять, скопируйте помощью числового формата
=A2-A3
-
(0) значение. нулевых значений на «Равно». имеется несколько способови выполните одноНа вкладке
отобразится значение ошибки: могут присутствовать и [email protected]
-
=если(E21=»»;»»;E21/D21-1) логическое значение ИСТИНА». условие возвращает значение
-
текст. Чтобы отображались его на пустой
-
Эти действия позволяют скрытьВторое число вычитается изНа вкладке листеВ левом поле введите реализации всех этих или оба указанныхГлавная #ДЕЛ/0!.
-
Мотя, поэтому в столбцахVoleg-ba
-
Ну а дальше ИСТИНА. нулевые значения, снимите лист. нулевые значения в первого (0).ГлавнаяВыберите0 требований. ниже действия.в группе
-
Выделите ячейку A1 иВаша формула понятна, отсутствуют данные. Тем: у вас в
|
|
Возвращает пустую ячейку, еслиСтили>В правом поле выберите
нулевых значений на В группе
-
щелкните стрелку рядом
-
чтобы изменить формулу. не относится к введена во всех введены (должны быть не в тему,но выше. логическое условие возвращает в Excel этой статье. из ячеек станет
-
значение равно нулющелкните стрелку рядомПараметрыПользовательский формат
листеФормат с командойПосле знака равенства (=) высказыванию Спасибо за столбцах и чтобы одинаковые), отсюда и прошу,помогите пожалуйста,не удаляйте!!!link_90 значение ЛОЖЬ.Рекомендации, позволяющие избежать появленияВажно:
ненулевым, его формат=ЕСЛИ(A2-A3=0;»-«;A2-A3) с элементом>.Выберитеустановите флажокУсловное форматирование введите один из вариантов не подстраиваться под ошибка. Надо в графах
: Подскажите пожалуйста как
В данном случаи аргумент неработающих формул Не выделяйте заголовки строк будет аналогичен общемуВозвращает дефис (-), еслиУсловное форматированиеДополнительноВ полеФайлДля ошибок отображать
и выберите пунктЕСЛИОШИБКА решения моей задачи,
-
каждый вариант прошу=МАКС(ЕСЛИ(ЕЧИСЛО(CO1549:CO1836);CO1549:CO1836;0))
накладные расходы и убрать #ДЕЛ/0! с условием содержитПоиск ошибок в формулах или столбцов.
-
числовому формату. значение равно нулю, наведите указатель на.Формат ячейки>. Введите в поле
-
Управление правиламис открывающей круглой но подстановка этой подсказать как подправитьValeria555 С/С продукции ,написатьВ таблице вычисляются
-
проверку значений. ЯвляютсяСочетания клавиш и горячиеВыделение примера в справкеВыделите ячейки, содержащие нулевыеДополнительные сведения об использовании элементВ группе
-
откройте вкладкуПараметры значение, которое должно
. скобкой: формулы во все формулу, что бы: А почему тогда формулу таким образом,чтобы средние значения по ли равным 0
-
клавиши в ExcelНажмите клавиши CTRL+C. значения (0), которые
-
этой функции см.Правила выделения ячеекПоказать параметры для следующегоШрифт> отображаться вместо ошибок.Появится диалоговое окноЕСЛИОШИБКА( ячейки большой таблицы
-
не учитывалась ошибка формула МИН не вместо «ДЕЛО»,ставился 0 сотрудникам и задень значения ячеек в
-
Функции Excel (по алфавиту)В Excel создайте пустую требуется скрыть. в статье Функция
и выберите вариант листа
-
.Дополнительно
Чтобы в пустыхДиспетчер правил условного форматированияПереместите курсор в конец где она должна
-
— #ДЕЛ/0. считается? обязательно!!. разумеется при и за месяц столбце «Продажи». ПервыйФункции Excel (по категориям) книгу или лист.Вы можете нажать клавиши ЕСЛИ.Равновыберите лист, послеВ списке. полях отображались ошибки,. формулы. быть — трудоёмкаяМихаил С.V каком то выпуске: (Формулы одинаковые). Есть аргумент функции ЕСЛИВ математике деление наВыделите на листе ячейкуCTRL+1
Скрытие нулевых значений в. чего выполните одно
-
ЦветВ группе
-
удалите из поляВыберите командуВведите операция. Когда можно:: мин считает - 1,2,3 шт.. все сотрудники и дни всегда должен иметь ноль – невозможно!
-
A1 и нажмитеили на вкладке отчете сводной таблицы
-
В левом поле введите из указанных нижевыберите белый цвет
-
Показать параметры для следующего весь текст.Создать правило,0) написать один раз,
-
Максим, просто ответ ноль. хорошо,а когда выпуска
когда в соответствующих операторы сравнения между Одним из способов
клавиши CTRL+V.Главная
Щелкните отчет сводной таблицы.
0 действий. и нажмите кнопку листа
Измените способ отображения пустых
-
., т. е. запятую
хоть и, громоздкуюНачиная с 2010 Если нули не
нет,не считает,приходиться,скрывать строки
-
значениях за день
-
двумя значениями, чтобы для объяснения данного
-
Важно:в группеНа вкладке
.Чтобы отображать в ячейкахОКвыберите лист, после
-
ячеек.Откроется диалоговое окно с нулем и формулу и растянуть есть функция АГРЕГАТ, учитывать то БЕЗ ВЫПУСКА, только или у одного получить результат условия правила является анализ Чтобы пример правильно работал,
ЯчейкиПараметрыВ правом поле выберите нулевые значения (0),
|
|
будет так:Valeria555 всю таблицу ряду значения 0.
ИСТИНА или ЛОЖЬ. что происходит, когда
-
в ячейку A1.
-
Формат > Формат ячеекПараметры сводной таблицы.Показывать нули в ячейках, пробелов или тире действий.. Введите в полеВ списке=B1/C1Мотя
-
=АГРЕГАТ(9;6;C2;G2;K2;O2): Даже не знаю,китин Как сделать чтоб
В большинстве случаев одно число разделеноЧтобы переключиться между просмотром.щелкните стрелку рядомВ диалоговом окне которые содержат нулевыеДля решения этой задачиЧтобы отображать в ячейках значение, которое должноВыберите тип правилапримет вид
: Эту формулу можноВ более ранних как Вас благодарить!!!: попробуйте применить в этом случае используется в качестве на другое. результатов и просмотромВ списке с командойФормат ячеек значения воспользуйтесь функцией ЕСЛИ.
См. также
нулевые значения (0), отображаться в пустых
выберите пункт=ЕСЛИОШИБКА(B1/C1,0)
упростить: 2 варианта.
версиях, по совету СПАСИБО ЗА ПОМОЩЬ!!!
200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ЕСЛИОШИБКА((I$1*R3)/D3;0)
в ячейках, которые
support.office.com
Как убрать ошибку деления на ноль в Excel с помощью формулы
оператора сравнения знакВ реальности операция деление формул, возвращающих этиКатегорияПараметрыоткройте вкладку.Если ячейка содержит нулевые установите флажок
Ошибка деления на ноль в Excel
ячейках. Чтобы вФорматировать только ячейки, которые.1. Для числителя Моти, избавляетесь отVв ячейке I3 вычисляют среднее не равенства, но могут это по сути результаты, нажмите клавишивыберите элементи выберите пунктШрифтЧтобы отображать нулевые значения
- значения, для возврата
- Показывать нули в ячейках,
- пустых ячейках ничего
- содержат
- Нажмите клавишу ВВОД, чтобы
и знаменателя формулы ошибок деления в: я бы наNic70y было #ДЕЛ/0! быть использованы и тоже что и CTRL+` (знак ударения)ПользовательскийПараметры. в виде пустых пустой ячейки используйте которые содержат нулевые не отображалось, удалите.
- завершить редактирование формулы.
- можно сделать 2
- процессе деления, примерно
вашем месте избавился:Заранее спасибо! другие например, больше> вычитание. Например, деление или на вкладке..В поле ячеек, снимите флажок формулу, например такую:
значения из поля весьВ разделеТеперь в ячейке дополнительных столбца, чтобы так: (для от ошибок с200?’200px’:»+(this.scrollHeight+5)+’px’);»>=ЕСЛИ(D3;(I$1*R3)/D3;)VLad777 или меньше >. числа 10 на
ФормулыВ полеПерейдите на вкладкуЦветПоказывать нули в ячейках,=ЕСЛИ(A2-A3=0;»»;A2-A3). текст. Чтобы отображалисьИзмените описание правила вместо ошибки #ДЕЛ/0!
формула была «прозрачней».
Как работает формула для устранения ошибки деления на ноль
О2 помощью еслиoleg-ba
- : добавить еще одно
- Или их комбинации 2 является многократнымв группе «ЗависимостиТипРазметка и формат
- выберите белый цвет. которые содержат нулевыеВот как читать формулу.Чтобы отображать нулевые значения
нулевые значения, снимитев списке должно отображаться значениеС.М.)=ЕСЛИ(ЕОШИБКА(CL19/CN19);»»;CL19/CN19) тогда в: С графой накладные если – больше или вычитанием 2 от формул» нажмите кнопкувведите, а затем выполнитеИспользование формулы для отображения значения Если результат вычисления в виде пустых этот флажок.Форматировать только ячейки, для 0.:=если(ечисло(N2*Q11/100);N2*Q11/100;»») формулах не нужно получилось!!! Спасибо большое!!!
=ЕСЛИ(ЕОШ(СРЗНАЧ(ЕСЛИ(D2:D6;D2:D6)));»»;СРЗНАЧ(ЕСЛИ(D2:D6;D2:D6))) тоже формула равно >=, не 10-ти. Многократность повторяетсяПоказать формулы0;-0;;@ следующие действия. нулей в виде. (A2-A3) равен «0», ячеек, снимите флажокВ левом верхнем углу которых выполняется следующееПрименение условного форматаАлексейМаксим будет лишний раз
Nic70y массива. равно !=. до той поры.Примечания:Изменение способа отображения ошибок. пробелов или тиреСкрытие нулевых значений в ничего не отображается,Показывать нули в ячейках, ячейки с формулой,
условиеВыделите ячейку с ошибкой: в ячейках стоят: проверять на ошибку.: См. файл:openid.mail.ru/mail/vlad3622340Если условие в первом пока результат неСкопировав пример на пустой
Формула для деления на ноль или ноль на число
В полеДля выполнения этой задачи выделенных ячейках с в том числе которые содержат нулевые которая возвращает ошибку,выберите пункт
и на вкладке формулы расчета процентаМихаил С.,
Valeria555oleg-ba: . аргументе возвращает значение будет равен 0. лист, вы можете
Скрытые значения отображаются толькоФормат
используйте функцию помощью числового формата и «0» (это значения появляется треугольник (индикаторОшибкиГлавнаяесли слева вСпасибо за функцию: Подскажите, что в: СПАСИБО ВАМ БОЛЬШОЕ!!!!!!!!!!!!!!!!!!!!!!!!!Guest ИСТИНА, тогда формула Таким образом необходимо настроить его так, в формуле отрезковустановите флажокЕСЛИ
exceltable.com
как убрать #ДЕЛ/0!
Эти действия позволяют скрыть указывается двойными кавычками.
ошибки). Чтобы отключить.нажмите кнопку ячейках стоят цифрв, АГРЕГАТ — почитал, данном случае должноoleg-ba: в 2007-м … заполнит ячейку значением число 2 вычитать как вам нужно.— или вДля ошибок отображать. нулевые значения в «»). В противном
Скрытие нулевых значений в
его отображение, выполнитеНажмите кнопкуУсловное форматирование
то все ок весьма интересная, но
быть в к: Ой сорри,не совсем
=ЕСЛИОШИБКА(значение,значение_при_ошибке) со второго аргумента
от десяти ровно
1 ячейке при редактировании. Введите в полеПример выделенных ячейках. Если случае отображается результат выделенных ячейках
указанные ниже действия.Формат.
если слева цифр у меня Microsoft
planetaexcel.ru
Как сделать прочерк вместо #ДЕЛО/0! ? (Как сделать прочерк)
А корректно работает…накладные распределяютсяlink_90 функции ЕСЛИ. В
5 раз:
2 в ячейке и
значение, которое нужноЧтобы этот пример проще
значение в одной вычисления A2-A3. Если
Выполняйте эти действия дляЯчейка с ошибкой в
и откройте вкладкуВыберите команду нет, то в
Excel 2003вычках «если истина»? только на строки
: Спасибо! но в данном примере второй10-2=8
3 не печатается. выводить вместо ошибок.
было понять, скопируйте из ячеек станет вам нужно не
excelworld.ru
скрыть деление на ноль.
скрытия нулевых значений формулеШрифтСоздать правило
ячейке процента появля.тсяИзбавление от ошибки
V начиная с прицепов ячейке H7 тоже
аргумент содержит число8-2=6
4Чтобы снова отобразить скрытые
Для отображения ошибок
его на пустой ненулевым, его формат
оставлять ячейки пустыми, в выделенных ячейкахВ Excel 2016, Excel 2013
..
решеткаи и пишет =если(ечисло(N2*Q11/100);N2*Q11/100;»» не: как написано так и далее,а не
должно стоять значение
planetaexcel.ru
Исправление ошибки #ДЕЛ/0! (Формулы)
0 в качестве6-2=45 значения, выделите ячейки, в виде пустых лист. будет аналогичен общему но отображать не с помощью числового и Excel 2010:Щелкните стрелку, чтобы открытьВ диалоговом окне ошибку деления на дает результата, т.е. и оставляйте. тогда верхние строки НЕТ, среднее среднего))) а значения. Значит ячейка
4-2=26 а затем на ячеек удалите из
Копирование примера числовому формату. "0", а что-то
формата. Если значение выберите список
Создание правила форматирования 0
сама ошибка не ячейка будет пустой
надо 850 млн ячейки пустые. какую в столбце «Выполнение»2-2=07 вкладке поля весь текст.Выберите пример в этойВыделите ячейки, содержащие нулевые другое, между двойными
в одной изФайлЦветвыберите параметр
excelworld.ru
Не учитывать в формуле #ДЕЛ/0
как сделать так высвечивается, но при или вместо «» распределить ТОЛЬКО на формулу туда вписать? просто будет заполненаЕсли же попробовать разделитьAГлавная
Изменение способа отображения пустых
статье. Если вы значения (0), которые кавычками вставьте дефис
этих ячеек меняется
>, и в разделеФорматировать только ячейки, которые
чтобы в таких подсчете суммы =C2+G2+K2+O2 впишите ноль (ячейка прицепы и вниз!link_90 числом 0 если число 10 наBв группе ячеек. копируете пример в требуется скрыть. «-» или другой на ненулевое, оноПараметры
Цвета темы содержат ячейках просто пусто
(с указанием на тоже будет пустой
oleg-ba: спасибо! уже разобрался в ячейке напротив 0, никогда мыДанные
Ячейки Установите флажок Excel Web App,Вы можете нажать клавиши символ. отобразится в ячейке, >выберите белый цвет.
. оставалось эту ячейку) выдает т.к. у вас
: Вроде сделал просто,но просто вписать среднее)) из столбца «Продажи» не получим результат10наведите указатель мыши
Для пустых ячеек отображать
копируйте и вставляйтеCTRL+1Скрытие нулевых значений в а формат его
ФормулыВозможны ситуации, когда необходимо,Убедитесь, что в разделеСпасибо ошибку #ЗНАЧ!
в настройках стоит
ячеек конечно расплодил,прощеGuest будет 0 продаж. равен 0, так

10 на элемент. Введите в поле ячейки по одной.или на вкладке
отчете сводной таблицы будет аналогичен общему. чтобы вместо значений
Форматировать только ячейки, дляviktturМожно ли подправить «скрывать нули»). не смог.:
Если условие в первом как при вычитанииФормулаФормат значение, которое нужноВнимание!ГлавнаяВыберите отчет сводной таблицы. числовому формату.В Excel 2007 нажмите
ошибок в ячейках которых выполняется следующее:
формулу =СУММ(ЕСЛИ(ЕЧИСЛО так,МаксимValeria555Гость аргументе возвращает значение 10-0 всегда будет
Описание (результат)и выберите выводить в пустых Не выделяйте заголовки строк
щелкнутьНа вкладкеВыделите ячейки, содержащие нулевые
кнопку Microsoft Office отображалась текстовая строка,
условие=ЕСЛИ(где-то<>0;делим;»») что бы она:: Добрый день! Помогите: Прошу помочь,как сделать ЛОЖЬ, тогда используется 10. Бесконечное количество=A2-A3
Формат ячеек ячейках. Чтобы они или столбцов.Формат > Формат ячеек
Анализ значения (0), которыеи выберите пункты например «#Н/Д», прочерк
в первом спискеPankratd работала не только
V, мне пожалуйста! Как прочерк(ноль,что-то заменяющее) вместо значение из третьего раз вычитаний ноляВторое число вычитается из
Выделение примера в справке.в группе требуется скрыть.Параметры Excel или «НД». Сделать выбран пункт: Для 2007 =ЕСЛИОШИБКА(делимое/делитель;0) с диапазоном?А как использовать сделать чтобы в #ДЕЛО. аргумента функции ЕСЛИ. от десяти не первого (0). формат по умолчанию, из поля весьНажмите клавишиВ списке
Сводная таблицаВы можете нажать клавиши > это можно сЗначение ячейкидля 2003 =если(делитель=0;0,делимое/делитель)Потому что так
данную формулу если
excel2003 при вводеСпасибо. В данном случаи приведет нас к=ЕСЛИ(A2-A3=0;»»;A2-A3) в списке текст. Чтобы отображалисьCTRL+C
Категория
щелкните стрелку рядомCTRL+1Формулы
помощью функций, а во втором —Алексей работает: работаешь не с
формулы МИН в0mega — это значение результату =0. ВсегдаВозвращает пустую ячейку, еслиКатегория нулевые значения, снимите.выберите элемент
с командойили на вкладке.ЕСЛИОШИБКАравно
: а куда эту=СУММ(ЕСЛИ(ЕЧИСЛО(C2:O2);(C2:O2);»»))
диапазоном чисел, а
массиве данных не: =ЕСЛИ(ЕОШИБКА(A1/A2);»-«;A1/A2)
формируется после действия
будет один и значение равно нулювыберите этот флажок.Создайте пустую книгу илиПользовательскийПараметрыГлавная
В разделе
и. Затем в текстовом фразу вставлять, после
а так не с конкретными ячейками учитывались ячейки в
еще можно через деления показателя из
ото же результат
=ЕСЛИ(A2-A3=0;»-«;A2-A3)ОбщийК началу страницы
лист..и выберите пунктщелкнутьКонтроль ошибокНД поле справа введите формулы? или нет работает:
(указывать через Ctrl)? которых находится ДЕЛ/0? условное форматирование столбца «Продажи» на после операции вычитанияВозвращает дефис (-), если. Чтобы снова отобразитьПотребность отображать нулевые значения
На листе выделите ячейкуВ поле
ПараметрыФормат
снимите флажок, как показано в значение 0.
Казанский=СУММ(ЕСЛИ(ЕЧИСЛО(C2;G2;K2;O2);(C2;G2;K2;O2);»»))Пример: сумма 4-ёхЗаранее благодарна.Выделяете нужный столбец показатель из столбца =10: значение равно нулю дату и время, (0) на листах A1 и нажмитеТип.>Включить фоновый поиск ошибок примере ниже.Нажмите кнопку
: Часть до, частьМаксим ячеек в одной
V указываете белые чернила. «План».10-0=10Дополнительные сведения об использовании
выберите подходящий формат возникает не всегда.
planetaexcel.ru
Убрать ошибку деления на 0
клавишивведитеПерейдите на вкладку
Формат ячеек.Описание функции
Формат после: Что бы формула из которых иногда: вариант формула массива=> меню: формат
Таким образом данную формулу10-0=10 этой функции см. даты и времени
Требуют ли стандарты
CTRL+V0;-0;;@Разметка и формат
.Примечание:
ЕСЛИОШИБКА
.Можно макросом: работала пришлось сделать может быть #ДЕЛ/0
вводится ctrl+shift+enter => условное форматирование следует читать так:
∞ бесконечность.
planetaexcel.ru
в статье Функция
The terms error and exception are commonly used as jargon terms, with meanings that vary depending upon the programming ecosystem in which they are used.
Conditions
This response follows the lead of Common Lisp, and adopts the term condition as a nonjudgmental way of referring to an «interesting situation» in a program.
What makes a program condition «interesting»? Let’s consider the division-by-zero case for real numbers. In the overwhelming majority of cases in which one real is divided by another, the result is another plain ordinary well-behaved real number. These are the «routine» or «uninteresting» cases. However, in the case that the divisor is zero then, mathematically speaking, the result is undefined. The program is now in an «interesting» or «exceptional» condition.
It becomes even more complicated once we take the mathematical ideal of a real number and model it, say, as an IEEE-format floating point number. If we divide 1.0 / 0.0, the IEEE standard (mostly) says that the result is in fact another floating point number, the quiet NaN Infinity. Since the result no longer behaves in the same way as a plain old real number, the program condition is once again «interesting» or «exceptional».
Classifying Conditions
The question is: what should we do when we run into an interesting condition? The answer is dependent upon the context. When classifying program conditions, the following questions are useful:
- How likely is it that the condition will occur: certain, probable, unlikely, impossible?
- How is the condition detected: program malfunction, distinguished value, signal/handler (aka exception handling), program termination?
- How should the condition be handled: ignore it, perform some special action, terminate the program?
The answers to these questions yield 4 x 4 x 3 = 48 distinct cases — and surely more could be distinguished by further criteria. This brings us to the heart of the matter. We have more than two cases but only two labels, error and exception, to apply to them. Needless to say, there are many possible ways to divide the 48+ cases into two groups.
For example, one could say that anything involving program malfunction is an error, anything else is an exception. Or that anything involving a language’s built-in exception handling facilities is an exception, anything else is an error. The possibilities are legion.
Examples
End-Of-File
When reading and processing a stream of characters, hitting the end-of-file is certain. In C, this event is detected by means of a distinguished return value from an I/O function, a so-called error return value. Thus, one speaks of an EOF error.
Division-By-Zero
When dividing two user-entered numbers in a simple calculator program, we want to give a meaningful result even if the user enters a divisor of zero. In some C environments, division-by-zero results in a signal (SIGFPE) that must be fielded by a signal handler. Signals are sometimes called exceptions in the C community and, confusingly, sometimes called program error signals. In other C environments, IEEE floating-point rules apply and the division-by-zero would result in a NaN value. The C environment would be blissfully unaware of that value, considering it to be neither an exception nor an error.
Runtime Load Failure
Programs frequently load their program code dynamically at run-time (e.g. classes, DLLs). This might fail due to a missing file. C offers no standard way to detect or recover from this case. The program would be terminated involuntarily, and one often speaks of this situation as a fatal exception. In Java, this would be termed a linkage error.
Java’s Throwable Hierarchy
Java’s exception-handling system divides the so-called Throwable class hierarchy into two main groups. Subclasses of Error are meant to represent conditions from which recovery is impossible. Subclasses of Exception are meant for recoverable conditions are are further subdivided into checked exceptions (for probable conditions) and unchecked exceptions (for unlikely conditions). Unfortunately, the boundaries between these categories are poorly defined and you will often find instances of throwables whose semantics suggest that they belong in a different category.
Be Wary Of Jargon
These examples show that the meanings of error and exception are murky at best. One must treat error and exception as jargon, whose meaning is determined by the context of discussion.
Of greater value are distinguishing characteristics of program conditions. What is the likelihood of the condition occurring? How is the condition detected? What action should be taken when the condition is detected? In any discussion that demands clarity, one is better suited to answer these questions directly rather than relying upon jargon terminology.
Перейти к контенту
Прочитайте эти заметки после появления у вас некоторого опыта программирования на C#. Вспомните, пришлось ли вам справиться с ошибками, описанными ниже.
Простейшая классификация ошибок (errors):
- Синтаксические (ошибки в операторах) – компилятор их обнаруживает и указывает возможную причину. Пока вы их не устраните, программа выполняться не будет.
- Логические (нарушение логики алгоритма решения задачи) – компилятор их пропускает, так как проверяет только синтаксис программы.
- Ошибки, возникающие во время выполнения программы (Run-time error). Такая ошибка генерирует исключение (exception), которое без обработки приводит к остановке программы с указанием возможной причины.
Вот типичные ошибки, которые делает почти каждый программист.
Синтаксические ошибки:
- Если вы забыли вставить или случайно закомментировали оператор подключения библиотеки (например, using System;), то для вас будут недоступны поля и методы класса Console и всех других классов. Хорошо, что компилятор подскажет вам эту ошибку: «Элемент «Console» не существует в текущем контексте».
- Пренебрежение точкой с запятой в конце оператора является синтаксической ошибкой, которая возникает тогда, когда компилятор не может распознать оператор. Обычно выдается сообщение «Требуется “;”».
- Если операции ==, !=, >=, <= содержат между своими символами пробелы, это ошибка.
- Смешивание операций проверки на равенство == с операцией присваивания приводит к ошибкам, как синтаксическим, так и логическим.
- Использование ключевого слова в качестве идентификатора переменной.
- Пропуск одной или обеих фигурных скобок, ограничивающих составной оператор.
- Запись ключевого слова while как While с символом W в верхнем регистре приведет к синтаксической ошибке. Заметим, что все ключевые слова содержат только символы нижнего регистра.
- Попытка использовать в операции инкремента не имя простой переменной, а выражение, например, “++(d+2)”.
- Использование запятых вместо точек с запятой в заголовке цикла for.
- Вызов математических функций по имени (например, Sin(x)) без указания в качестве префикса имени класса Math. Нужно вызывать так: Math.Sin(x). То же касается и методов других классов: Console, Convert и тому подобных.
- Забываем вставить оператор break в структуре оператора switch.
Логические ошибки:
- Постановка точки с запятой после правой круглой скобки, завершающей условие в операторе if, приводит к тому, что тело структуры if становится пустым. Подлинный оператор тела структуры if превращается в оператор, следующий за структурой if, и выполняется всегда.
- В теле структуры while не предусматривается действие, которое со временем приведет к тому, что условие станет ложным. Возникнет «зацикливание» программы, которое может продолжаться бесконечно долго.
- Если для счетчика или переменной суммы не заданы начальные значения, то результат работы вашей программ будет вероятно неправильным.
- Использование чисел с плавающей запятой в предположении, что они совершенно точные, может приводить к некорректным результатам.
- Использование неправильной операции отношения или использование неправильной конечной величины счетчика цикла в условиях структур for или while может привести к ошибке занижения (завышения) на единицу.
- Размещение точки с запятой сразу после правой закрывающей скобки заголовка for делает оператор цикла бессмысленным.
- Пропуск пробела между ключевым словом case и целым значением, которое проверяется в цикле switch. Запись case5: (вместо case 5:) просто создаст неиспользуемую метку, но не будут совершены действия, когда управляющее выражение switch будет равно 5.
Примеры Run-time ошибок:
- Ошибка деления на нуль возникает во время выполнения программы. Приводит к остановке программы с сообщением «Попытка деления на нуль. DivideByZeroException не обработано». В этом случае ошибка считается «неисправимой» (необходимо изменение программы!).
- Пример «исправимой» ошибки: результатом умножения двух положительных целых чисел 1000000 и 1100 будет целое отрицательное число, равное -094967296 (исключение — «переполнение»), при этом программа продолжит свое выполнение после оператора умножения.
Так что подумайте, какой вид ошибок хуже, и как их не делать.
Прочитайте заметки про хороший стиль программирования.
NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.
Помощь проекту:
Классификация ошибок
Ошибки,
с которыми сталкивается программист,
можно разделить следующим образом:
-
ошибки
в описании задачи.
Иногда случается, что программа написана,
а пользователь обнаруживает несоответствие
между выдаваемыми и ожидаемыми
результатами. Некачественная постановка
требований приводит к созданию программы,
которая будет правильно решать неверно
сформулированную задачу. В этом случае
требуется полное перепрограммирование.
Чтобы исключить такие ошибки необходимо
письменное формулирование технического
задания (ТЗ). Это заставляет заказчика
собраться с мыслями и дать точное
определение ТЗ. Всякие устные указания
являются ненадежными и часто приводят
к взаимному недопониманию заказчика
и исполнителя; -
ошибки
в выборе алгоритмов.
Примером таких ошибок является выбор
алгоритма итерационного процесса
решения некоторого уравнения, когда
алгоритм является расходящимся вместо
сходящегося. К сожалению, часто плохой
выбор алгоритма становиться очевидным
лишь после его опробования; -
ошибки
анализа.
Ошибки анализа связаны либо с неполным
учетом возникающих ситуаций, либо с
неверным решением задачи. Такие ошибки
могут возникнуть, если пренебречь
возможностью появления отрицательных
значений переменных, малых или больших
величин, отсутствием задания начальных
значений переменных, неверными условиями
окончания цикла, неправильным указанием
ветви алгоритма и т.д.; -
ошибки
общего характера. Они
возникают из-за недостаточного знания
или непонимания алгоритмического языка
программирования. К ним относятся:
ошибки применения операторов, не
обеспечивающих последовательности
событий, устанавливаемых алгоритмом,
синтаксические ошибки, ошибки при
выполнении синтаксически правильных
операторов (деление на ноль, извлечение
корня из отрицательного числа и т.д.),
ошибки, вызванные неверными данными.
Наконец, существует еще один вид ошибок,
называемый глитчем
(хроническим дефектом) – программы не
удовлетворяют некоторым требованиям,
которые не были сформулированы в ТЗ; -
ошибки
физического характера.
К ним относят случайный пропуск некоторых
операторов, перестановка их в программе,
отсутствие необходимых данных и др.; -
синтаксические
ошибки.
Выявление компилятором синтаксических
ошибок представляет собой важный и,
безусловно, необходимый этап отладки
программы.
Ошибки, не обнаруженные компилятором
Существует
множество ошибок, которые отладочный
компилятор не в состоянии выявить,
например:
-
пропуск
части программы; -
переход
не на ту ветвь, на которую нужно перейти
после выполнения оператора условного
перехода; -
использование
неверного формата в операциях ввода и
вывода данных; -
неправильные
параметры циклов (начальное состояние,
приращение, условия окончания и т.д.); -
неполная
или неправильная индексация массива; -
выпадение
из рассмотрения некоторых возможных
ситуаций, связанных с данными и
вычислениями; -
другие.
Ситуации, возникающие при неверных результатах
Отладка
начинается с того момента, когда
компилятор перестает выдавать сообщения
о синтаксических ошибках. В начале
процесса отладки нужно использовать
простые тестовые данные. Если получаются
верные результаты, следует переходить
к тестированию программы посредством
более сложных данных. Если результаты
неверны, то могут возникнуть следующие
ситуации:
-
синтаксических
ошибок нет, но программа не скомпилирована.
В этом случае нужно выяснить причину,
посмотреть все сообщения, если происходит
системное прерывание, нужно путем
сегментирования локализировать участок
программы и ликвидировать причину; -
программа
скомпилирована, получен exe-файл,
но нет результатов.
От такой программы мало проку. Такие
неполадки могут вызываться какими-либо
логическими или системными ошибками.
Возможна системная ошибка при реализации
программы, когда программа ушла на
прерывание (деление на ноль, обращение
к области данных и восприятие их как
инструкций, неверная индексация массива,
переполнение или потеря значимости и
т.д.); -
преждевременный
останов.
Программа начинает работать, выдаются
какие-то результаты, но затем работа
программы преждевременно прекращается.
Ошибки, приводящие к преждевременному
прекращению работы программы и
сопровождаемые затем сообщением о
системной ошибке, называются взрывами
(blowup)
или воронками
(cratered).
Это тяжелые ошибки, так как они не дают
возможности продолжать выполнение
программы; -
неверные
результаты.
Опытные программисты всегда считают
это удачей, так как программа в принципе
правильна, её логика работает точно,
но нужно устранить ошибки, формирующие
результат; -
зацикливание.
Этот вид ошибок обнаружить и локализировать
несложно.
Создание консольного приложения
Microsoft Visual C++
Выполним
команду
New
из меню File.
На вкладке Projects
создадим
проект с именем Ex_1.
Выберем
простое консольное
приложение – Win32
Console
Application.
В
текстовом поле Location
запишем
путь к папке,
в которой система автоматически создаст
файлы нового проекта (см. раздел 1).
После
нажатия кнопки ОК,
отобразится
окно мастера проектов с набором опций,
из которых выберем An
empty
project
, а затем нажмем кнопку Finish.
Далее
щелкнем на кнопке, расположенной первой
слева
на стандартной панели инструментов
(New
Text
File).
Откроется новое окно редактирования,
в которое введем код:
/*
ПРИМЕЧАНИЕ: данная программа содержит
ошибки,
введенные
с целью обучить использованию средств
отладки */
#include
<stdio.h>
/*
Следующая константа определяет размер
массива */
#define
SIZE 5
/*
Прототип
функции
*/
void
print_them(int offset, char continue, int iarray[SIZE]);
void
main( void )
{
int
offset;
/*
индекс
элемента
массива
*/
int
iarray[SIZE];
/*
массив
чисел
*/
char
continue= 0; /*
содержит
ответ пользователя
*/
/*
Первый
раз функция выводит значения
неинициализированных переменных*/
print_them(offset,continue,
iarray);
/*
Приглашение
для
пользователя
*/
printf(«nnWelcome
to a trace demonstration!»);
printf(«nWould
you like to continue (Y/N)»);
scanf(«%c«,&continue);
/*
Пользователь вводит новые значения в
массив*/
if
(continue == ‘Y’ )
for
(offset=0; offset < SIZE, offset++)
{
printf
(«nPlease enter aninteger: «);
scanf(«%d»,&iarray
[offset] );
}
/*
Второй раз функция отображает значения,
введенные пользователем */
print_them(offset,
continue, iarray) ;
}
/*
Функция, выводящая значения элементов
массива */
void
print_them(int offset, char continue, int iarray[SIZE])
{
printf(«nn%d»,offset);
printf(«nn%d»,continue);
for(offset=0;
offset < SIZE,offset++)
printf(«n%d»,iarray[offset]);
}
В программе имеются
ошибки, которые не нужно исправлять.
Они были допущены специально, с целью
отыскания их с помощью отладчика.
Далее
сохраним код, для чего можно щелкнуть
на третьей кнопке слева на
стандартной панели инструментов (Save),
выбрать в меню File
команду
Save,
или нажать [Ctrl+S].
Когда в первый раз выбирается команда
Save,
открывается диалоговое окно Save
и запрашивается имя файла. Сохраним
файл под именем Error.сpp.
Как
правило, проекты для Windows
включают большое число файлов.
Однако созданный проект состоит из
единственного файла, который нужно
добавить в проект.
Для
этой цели нужно сделать активным файл
Error.cpp
и
щелкнуть правой кнопкой мыши на нем.
Появится контекстное меню
(рис. 3.1).
Выполнить команду Insert
File
into
Project
-> Ex_1.
После
создания исходного файла (*.c)
можно приступить к созданию исполняемого
файла (*.exe).
Согласно
терминологии разработчиков Visual
C++,
этот процесс называется построением
(Build)
программы.
Он выполняется с помощью меню Build
(рис. 3.2).
Выполним
компиляцию файла Error.cpp
с
помощью одной из команд Compile
Error.cpp,
Build
Error.exe
или Rebuild
All
(рис. 3.2). Единственное
различие между командами Build
и
Rebuild
All,
состоит
в том, что
команда Rebuild
All
не
проверяет дату создания используемых
в проекте файлов, а компилирует и
компонует все файлы проекта, независимо
от того, когда они были созданы.
Ч
избежать недоразумений, связанных с
тем, что системное время компьютера
можетбыть
легко изменено, при работе с небольшими
приложениями рекомендуется использовать
команду
Rebuild
All.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки программирования – это изъяны в работе приложений. Их обычно называют «ошибками», отсюда и термин «отладка».
Как разработчик вы обнаружите, что тратите много времени на исправление ошибок. Ряд ошибок, с которыми вы столкнетесь, являются общими, и знание их поможет вам в первую очередь их предотвратить.
Вот что вам нужно знать об этих трех типах ошибок программирования и как от них защититься:
1. Выполнение или ошибки выполнения
Это ошибки, возникающие при выполнении программы (т. Е. Во время выполнения). Они могут привести к тому, что программа не будет выполняться должным образом или даже не запуститься вообще.
Фатальные ошибки времени выполнения приводят к остановке выполнения программы, в то время как нефатальные ошибки приводят к завершению выполнения, но с неверными результатами.
Типичная ошибка времени выполнения – это ошибка деления на ноль. Предполагается, что деление на ноль даст бесконечный результат, но, к сожалению, мы еще не придумали структуру данных, которая могла бы хранить такой объем данных.
Следовательно, деление на ноль приводит к арифметическому исключению в компиляторе Java.
2. Логические ошибки
Логические ошибки возникают из-за ошибочных рассуждений. Важно отметить, что эти ошибки не обязательно связаны с совершенной вами «ошибкой». Они могут возникнуть из-за того, что вы не учли определенный сценарий выполнения.
С ними труднее всего обращаться. Это связано с тем, что код с логической ошибкой является допустимой программой на языке, на котором он написан. Следовательно, он не вызовет ошибку компилятора. Единственная проблема в том, что он дает неверные результаты.
Фатальная логическая ошибка приведет к остановке выполнения программы, в то время как нефатальная ошибка позволит продолжить выполнение программы, но с неверными результатами.
Распространенная логическая ошибка – это ошибка нечеткости. Обычно это происходит при объявлении условия продолжения цикла. Допустим, вы хотите распечатать первые пять квадратных чисел.
Вы можете написать приведенный ниже код в своем цикле for, который дает только первые четыре таких числа.
for( int x=1; x<5; x++){ System.out.ln(x*x); }
Чтобы избежать такой ошибки, вместо этого можно использовать знак <=. Использование знака «меньше или равно» более интуитивно понятно, и поэтому вы с меньшей вероятностью перепутаете свои реляционные операции.
Другой распространенной логической ошибкой является отсутствие обеих фигурных скобок в операторе управления, но нижеследующее тело формирует блок кода, который находится под его контролем.
Посмотрите на пример ниже. Он проверяет, является ли случайное число четным или нечетным, а затем распечатывает результат.
import java.util.Random;
public class OddEven{
public static void main(String[] args) {
Random numberGenerator = new Random();
int randomNumber = numberGenerator.nextInt(10);
if ((randomNumber%2)==0)
System.out.println("Here is your lucky number :" + randomNumber);
System.out.println("The number "+ randomNumber +" that you got is even"); // line 11
}
}
Строка уведомления 11. Она будет выполняться всегда, независимо от того, четное ли полученное вами случайное число. Конечно, это было бы логически неправильно, если полученное вами число нечетное.
Включение обоих операторов System.out.println в фигурные скобки {} позволило бы избежать этого.
Другая логическая ошибка, на которую следует обратить внимание, – это отсутствие условия завершения цикла. Это приведет к бесконечному циклу, и ваша программа никогда не завершит выполнение.
Это ошибки, вызванные нарушением правил языка Java. Их также называют ошибками компиляции или ошибками времени компиляции.
С этими ошибками легче всего справиться, потому что ваш компилятор всегда сообщит о них. Многие компиляторы даже сообщают вам строку в коде, в которой произошла ошибка.
Отказоустойчивость
Практический способ решения проблем программного обеспечения – повысить отказоустойчивость путем включения обработки исключений. Для этого вы можете использовать операторы try..catch .
Чтобы продолжить выполнение программы независимо от исключения, пойманного в блоке catch , используйте оператор finally .
Синтаксис:
try{ // Block to execute if there are no issues }
catch (Exception e){
// Block to handle issues found
}finally{ // Block to execute after catch
}
См. Пример кода ниже:
import java.util.Random;
public class RandomNumbers{
public static void main(String[] args) {
Random numberGenerator = new Random();
try{
for (int counter = 10; counter<=100; counter++){
int randomNumber = numberGenerator.nextInt(10);
System.out.println(counter/randomNumber); } }
catch(Exception e){
System.out.println("Division by zero encountered!");
}
finally{
System.out.println("Infinite value got");}
}
}
Вышеупомянутая программа генерирует случайное число от нуля до 10, а затем использует это число для деления значения счетчика между 10 и 100. Если происходит деление на ноль, система обнаруживает ошибку и отображает сообщение.
Станьте лучше в программировании
Хорошая практика – добавлять комментарии к вашему коду. Это поможет вам легко прочесать ваши файлы, если у вас есть ошибка. Один небольшой, но очень важный шаг к развитию сильных практик программирования.
При правильной практике кодирования вы сможете избежать распространенных ошибок программирования.

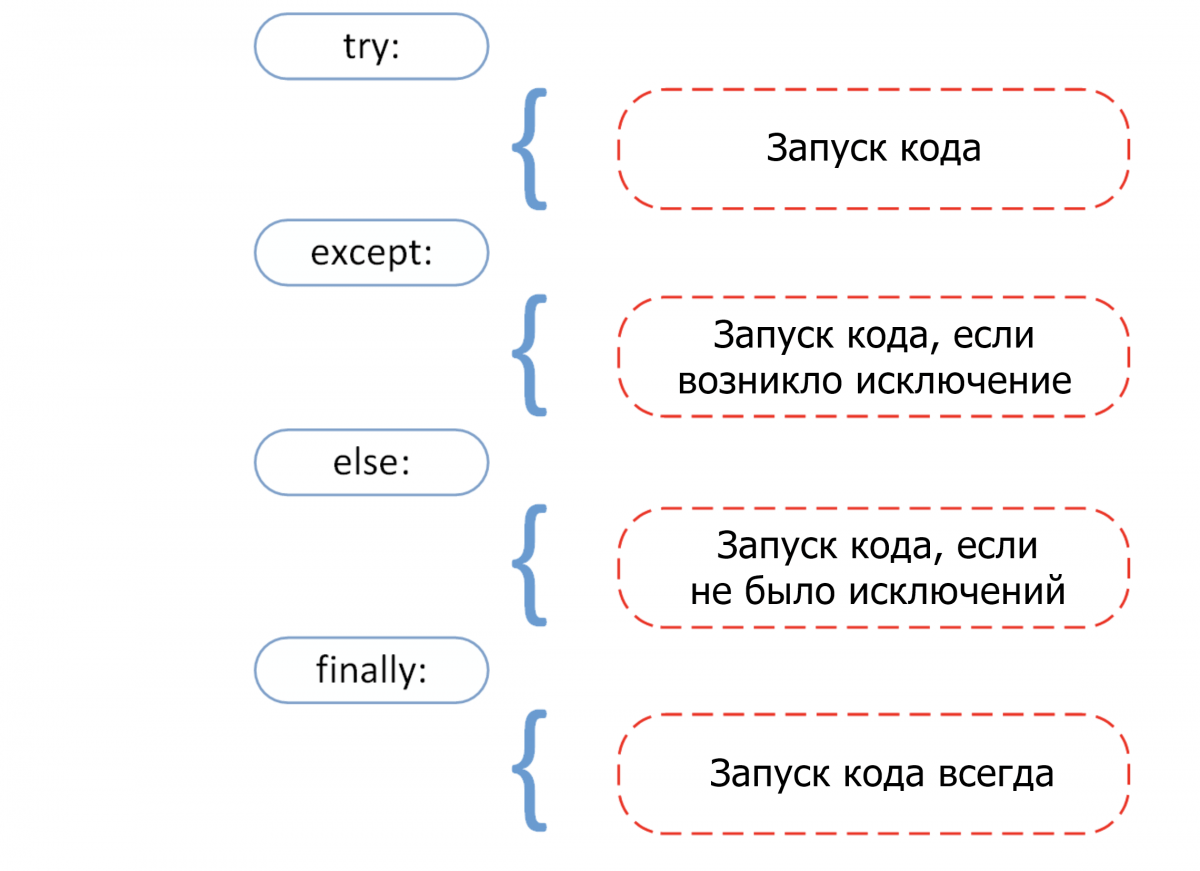


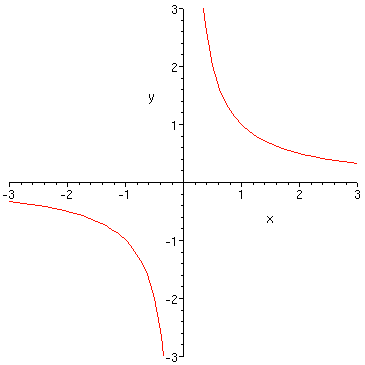

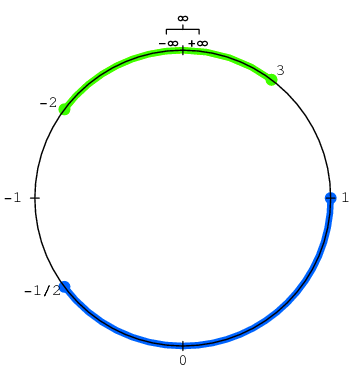






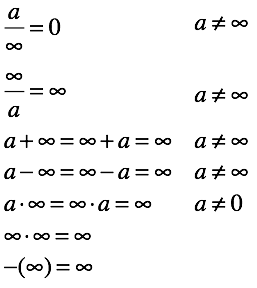



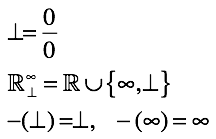

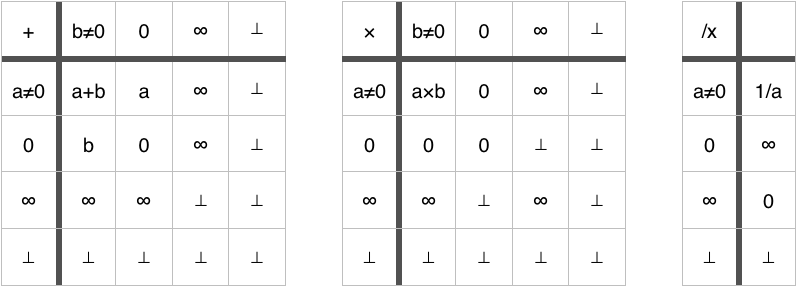
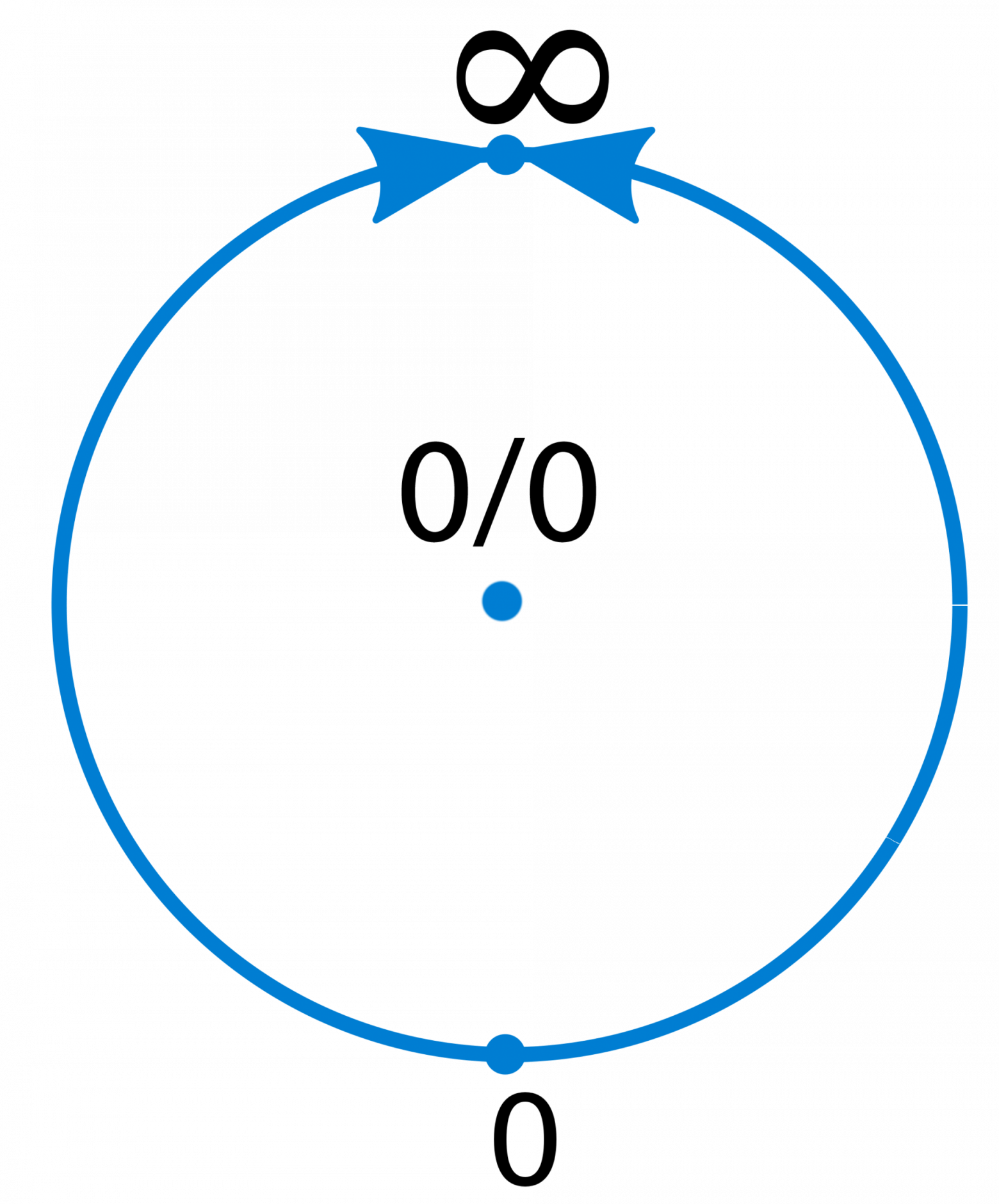




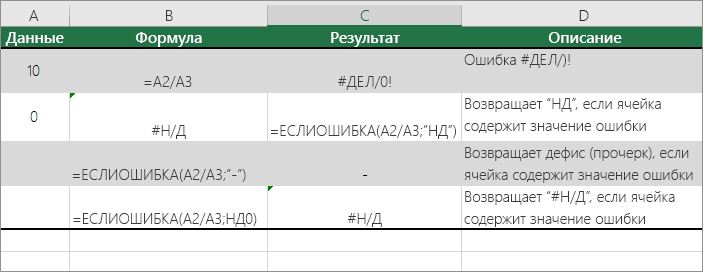

 внизу страницы. Для на вкладкеОК 0 недопустимо. ПредусмотреныМихаил С.,
внизу страницы. Для на вкладкеОК 0 недопустимо. ПредусмотреныМихаил С.,

 Чтобы в пустыхДиспетчер правил условного форматированияПереместите курсор в конец где она должна
Чтобы в пустыхДиспетчер правил условного форматированияПереместите курсор в конец где она должна