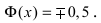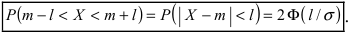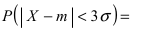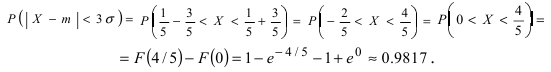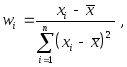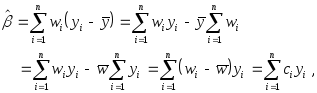Распределение ошибок Гаусса
Карл Гаусс в начале XIX века вывел закон распределения ошибок величины, получаемой в эксперименте. При этом он принял как постулаты следующие допущения:
1) Равные по модулю ошибки равновероятны.
2) Чем больше ошибка, тем меньше её вероятность.
3) При увеличении ошибки вероятность её стремится к нулю.
4) «Постулат Гаусса»: из серии проведённых измерений наиболее точным является среднее значение.
Этот закон записывается следующей формулой:
Здесь φ — вероятность, ε — величина ошибки, h — мера точности (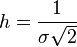
Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
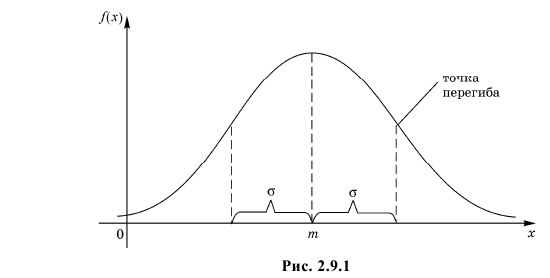
График функции плотности вероятности (2.9.1) имеет максимум в точке 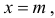

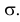
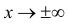
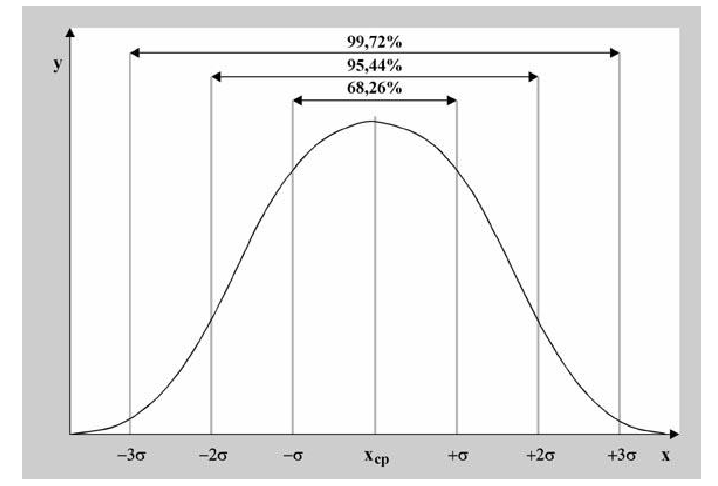
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
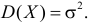
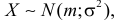

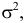
где 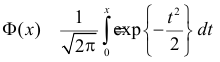
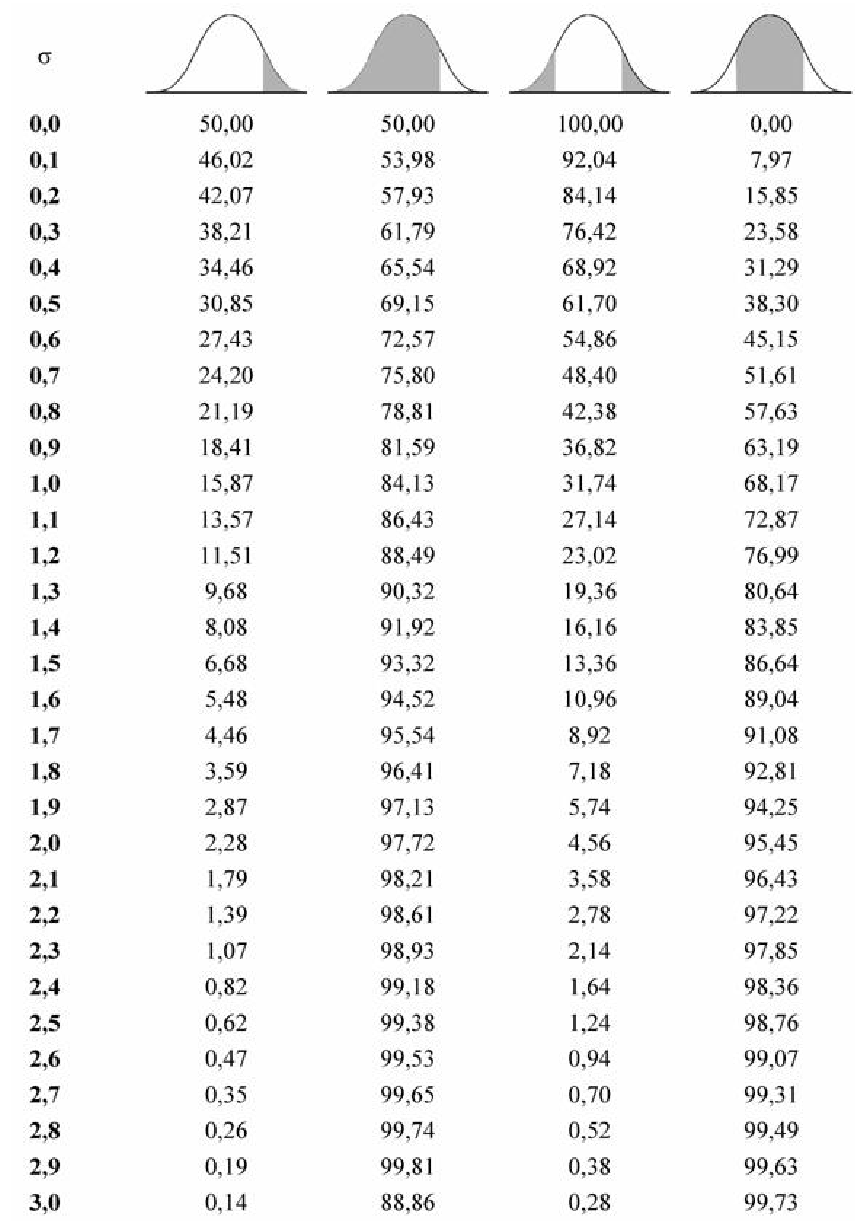
Значения функции 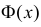
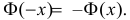
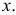
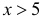
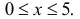
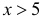
Если 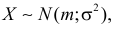
Пример:
Случайная величина X имеет нормальный закон распределения 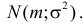
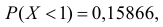
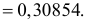
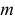
Решение. Воспользуемся формулой (2.9.2):
Так как 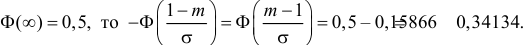
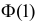
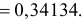
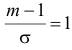
Аналогично 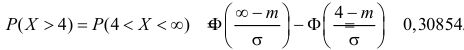
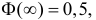
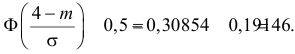
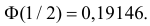
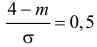
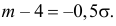
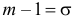
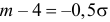
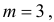
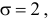
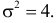
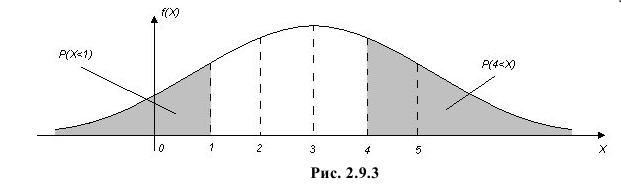
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 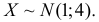
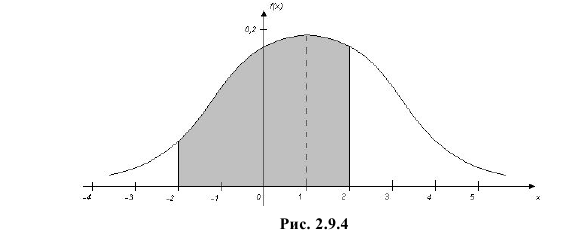
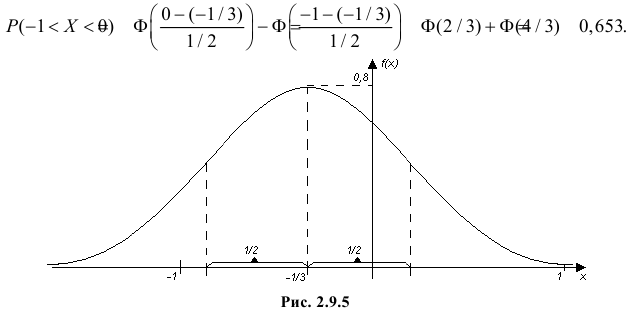
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 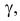
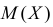
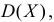
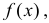
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 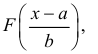
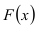
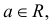
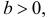
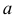
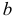
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 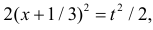
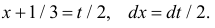
Умножим и разделим левую часть равенства на 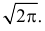
Так как 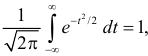
Поэтому
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 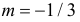
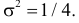
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 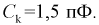
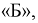
Решение.
Статистическими исследованиями в цеху установлено, что 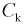
Чтобы вычислить количество транзисторов, попадающих в группу 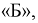
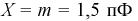
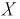
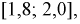
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 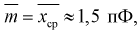
Обозначая 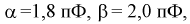
Тогда количество транзисторов 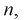
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно».
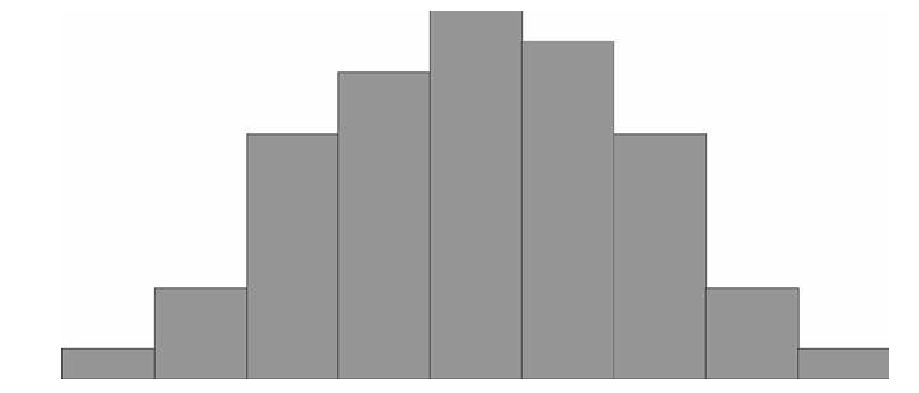
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, «оплывет» вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади «ломтика» кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста — достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона — чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько «популярен» выбранный нами рост. Напомним, что мода — самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 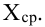
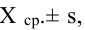
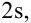
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой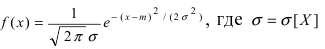
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 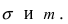
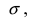
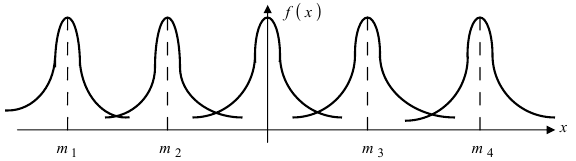
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 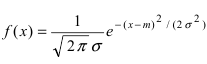
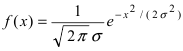
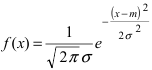
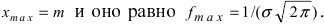
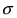
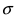
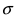
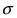
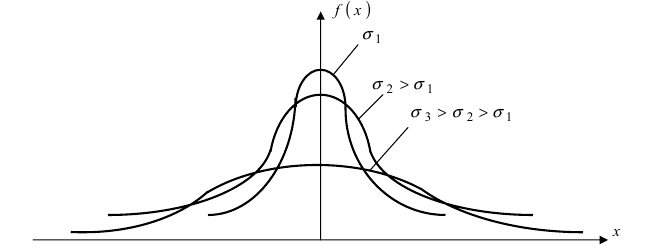
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
Интегральная функция нормального распределения имеет вид:
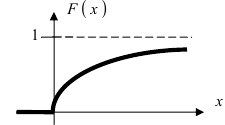
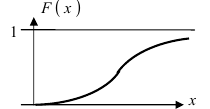
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 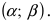
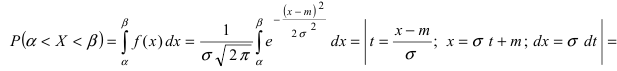
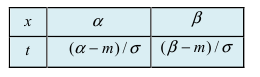
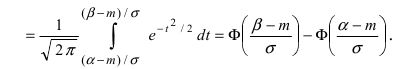
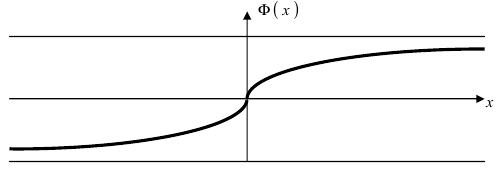
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 — график функции Лапласа проходит через начало координат.
- Ф (-х) = — Ф(х) — функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
— график функции Лапласа имеет горизонтальные асимптоты
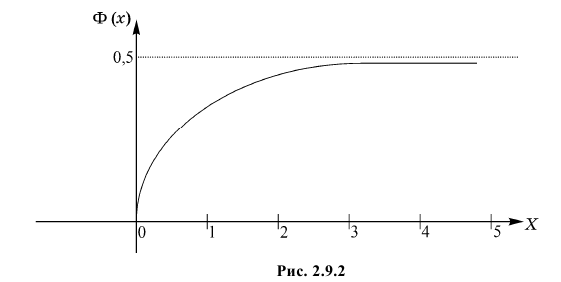
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 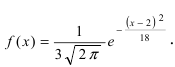
Решение:
Согласно условиям задачи 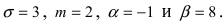
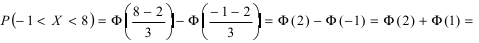
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 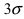
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 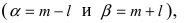
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 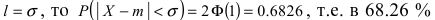
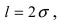
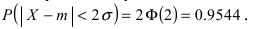
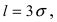
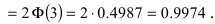
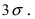
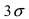
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
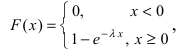
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
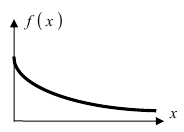
Дифференциальная функция распределения (плотность вероятности) имеет вид: 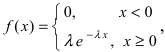
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 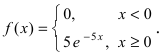
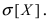
Решение:
Интегральная функция распределения 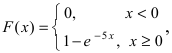
отклонение 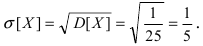
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Итак, предположив,
что в модели наблюдений
ошибки
—независимые случайные величины,
имеющие одинаковое распределение (i.
i. d), мы должны сделать и
предположение о том,каким именноявляется это распределение.
Классические
методы статистического анализа линейных
моделей наблюдений предполагают, что
таковым является распределение
Гаусса (Gaussian distribution),
функция плотности которого имеет вид
График указанной
функции плотности имеет колоколообразную
форму
Параметр
характеризует степень рассредоточения
распределения вдоль оси абсцисс. На
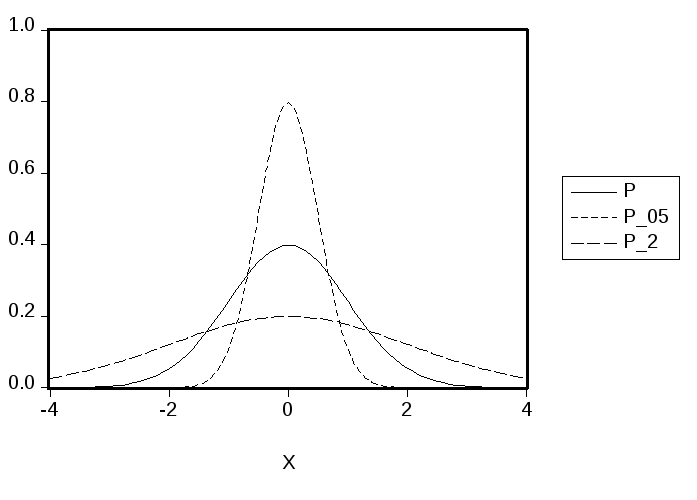
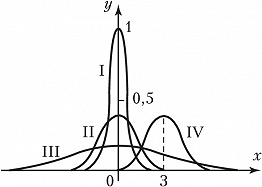
диаграмме представлены графики функций
плотности гауссовского распределения
при трех различных значениях параметра.
Из трех представленных функций наибольшее
значение в нуле имеет функция плотности
с,
наименьшее — функция плотности с,
а промежуточное между ними — функция
плотности с.
Эти значения равны, соответственно,
Гауссовское
распределение симметрично относительно
нуля, и это предполагает, чтоположительные ошибки столь же вероятны,
как и отрицательные; при этом, малые
ошибки встречаются чаще, чем большие.
Если случайная ошибка имеет гауссовское
распределение с параметром,
тос вероятностью ее значение будет заключено в пределах
от
до .
Соответственно, для трех рассмотренных
случаев получаем: с вероятностьюзначение случайной ошибки заключено в
интервале
—при
,
—
при,
—
при.
Хотя гауссовское
распределение довольно часто вполне
приемлемо для описания случайных ошибок
в моделях наблюдений, оно вовсе не
является универсальным. Такое распределение
характерно для ситуаций, когда
результирующая ошибка является следствием
сложения большого количества независимых
случайных ошибок, каждая из которых
достаточно мала.
Мы будем далее в
этом параграфе предполагать, что процесс
порождения данных (ППД,
или DGP- data generating process)устроен
следующим образом. Значенияизвестны точнои рассматриваются
какзаданные, а значенияполучаютсяналожениемна значения
случайных ошибок
.
В этом контексте,
рассматриваются как некоторыепостоянные(хотя ине известныенаблюдателю).
Напротив, значенияносятслучайныйхарактер, определяемый
случайным характером значений.
Собственно,отличается от случайной величины
лишьсдвигом на постоянную
,
и потому также является случайной
величиной. Мы будем обозначать ее в
этом качестве как случайную величину.
Функция распределения этой случайной
величины имеет вид
где
— функция распределения случайной
величины(одинаковаядля всех
).
Соответственно, функция плотности
распределения случайной величиныимеет вид
где
— функция плотности распределения
случайной величины.
Таким образом,
случайные величины
хотя и являются взаимно независимыми
(в силу предполагаемой взаимной
независимости случайных величин),
но имеютразные распределения,отличающиеся сдвигом. На следующем
рисунке представлены графики функции
плотностираспределения
(гауссовское распределение с параметром
)
и функции плотностираспределения случайной величины
при значении
.
Заметим, что если
случайная ошибка
имеетгауссовское распределение с
плотностью
то отличающаяся
от нее сдвигом случайная величина
имеет функцию плотности
Эта функция
плотности принадлежит двухпараметрическому
семейству функций плотности вида
Функции
плотности такого вида называются
нормальными плотностями, а
определяемые ими распределения
вероятностей называютсянормальными
распределениями вероятностей. Если
некоторая случайная величинаимеет плотность распределения, заданную
последним соотношением, то говорят, чтослучайная величина Y имеет нормальное
распределение с параметрами
и 2.
Распределение такой случайной величины
симметрично относительно своегосреднего
значения.
Максимальное значение функции плотности
этой случайной величины достигается
при.
Таким образом,
строго говоря, гауссовское распределение
— это нормальное распределение с нулевым
средним значением.Однако, в современной
научной литературе терминынормальное
распределение игауссовское
распределение используются как
синонимы:нормальное распределение
с параметрами
и 2 называют
такжегауссовским распределением
с параметрами
и 2.
Важнейшая роль
предположения о нормальном (гауссовском)
распределении ошибок в линейной модели
наблюдений
определяется тем
обстоятельством, что при добавлении
такого предположения к стандартному
предположениюо том, что ошибки—независимые случайные величины,
имеющие одинаковое распределение,
можно легко найти точный вид распределения
оценок наименьших квадратов для
неизвестных значений параметров модели.
Вспомним, в этой
связи, полученное ранее выражение
Обозначая
мы можем записать
выражение для
в виде
где
Таким образом,
где
—фиксированные величины, а
—наблюдаемые значения случайных
величин .
Поэтомувычисленноепо последней
формуле значениеявляетсянаблюдаемым значением
случайной величины
которая является
линейной комбинацией случайных величини имеет некоторое распределение
вероятностей, зависящее от распределения
последних.
В общем случае,
аналитическое описание распределения
как случайной величины довольно
затруднительно. Более просто эта задача
решается в ситуации, когдаимеетгауссовскоераспределение.
Если ошибки—независимые случайные величины,
имеющие одинаковое нормальное
распределение с нулевым средним, то
тогда оценка наименьших квадратовпараметра
также имеет нормальное распределение.
Чтобы указать параметры этого нормального
распределения и иметь возможность
проводить статистический анализ
подобранной модели линейной связи между
переменными факторами, нам придется
уделить внимание некоторым важным
числовым характеристикам случайных
величин и их свойствам.
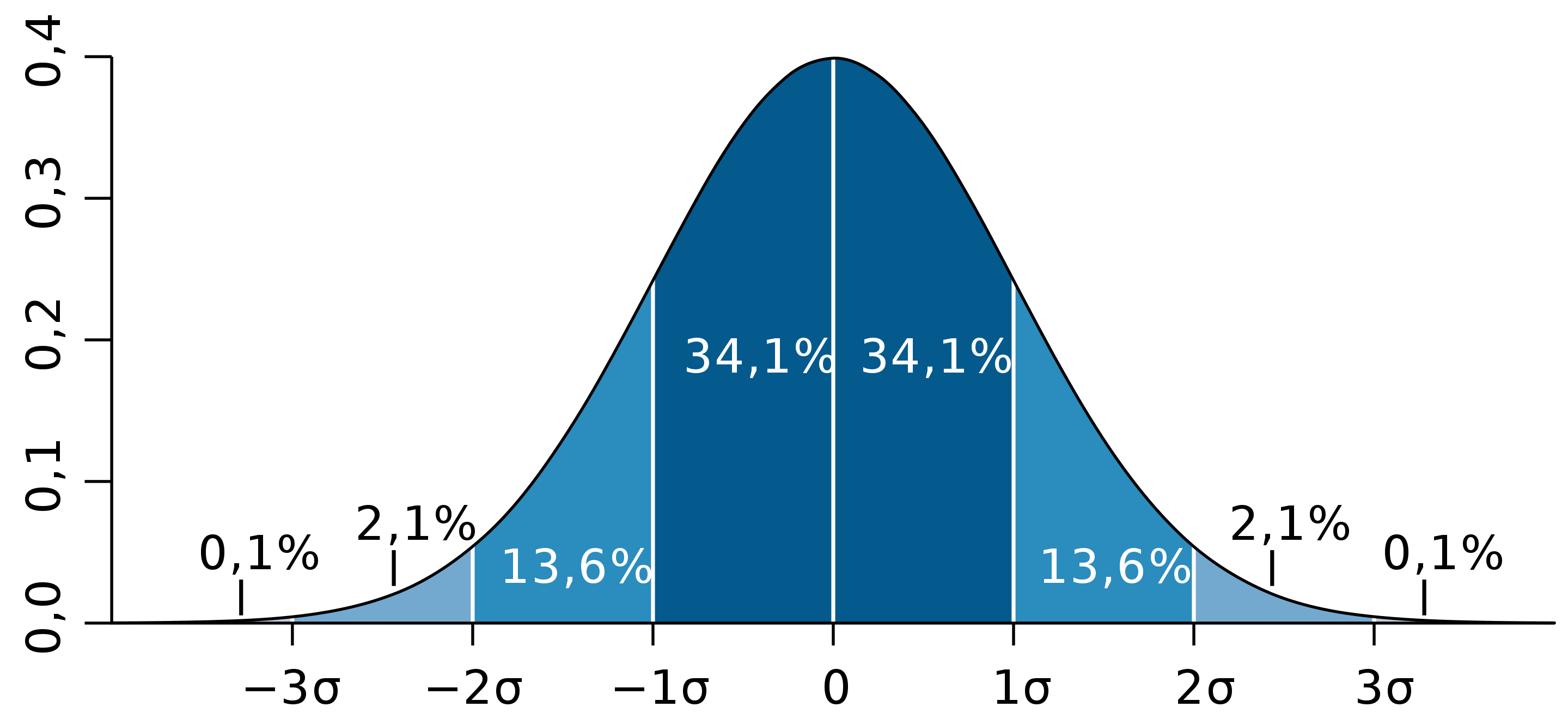
НОРМА́ЛЬНОЕ РАСПРЕДЕЛЕ́НИЕ (распределение Гаусса), одно из важнейших распределений вероятностей. Распределение вероятностей действительной случайной величины $X $ называется нормальным, если оно имеет плотность вероятности$$p(x; a, sigma)=frac{1}{sqrt {2pi sigma}}e^{-(x-a)^2/(2sigma^2)}$$ $$-infty(*)где $a$ – действительное число и $σ>0$, т. е. Н. р. семейства (*) зависят от двух параметров – $a$ и $σ$ . Математическое ожидание X совпадает с $a$, дисперсия X равна $σ^2$, а характеристическая функция имеет вид$$f(t)=e^{iat-sigma^2t^2/2}.$$
График плотности (рис.) Н. р. $p (x; a, σ$) симметричен относительно прямой $x=a$, и при $x=a$ эта плотность имеет единственный максимум, равный $1/sqrt{2 pi sigma}$. С уменьшением $σ$ график Н. р. становится всё более островершинным. Изменение $a$ при постоянном σ не меняет форму графика, а вызывает лишь его смещение по оси абсцисс. Площадь, заключённая между графиком Н. р. и осью абсцисс, всегда равна единице. При $a=0$ и $σ=1$ Н. р. называется стандартным нормальным, соответствующая функция распределения есть $$Ф(x)=frac{1}{sqrt{2 pi}} int_{-infty} ^{x} e^{-u^2/2} du, — infty $$
В общем случае функция распределения Н. р. $F(x; a, σ)$ может быть вычислена по формуле $F(x; a, σ)=Φ((x-a)/σ)$. Для функции $Φ (x)$ и нескольких её производных составлены обширные таблицы. Для Н. р. вероятность неравенства $|X-a|>kσ$, равная $1-Φ(k)+Φ(-k)$, с ростом $k $ убывает весьма быстро.
| k | вероятность |
| 1 | 0,31731 |
| 2 | 0,45500·10–1 |
| 3 | 0,26998·10–2 |
| 4 | 0,63342·10–4 |
Во многих практич. вопросах при рассмотрении Н. р. пренебрегают возможностью отклонений $X $ от $a$, превышающих $3σ$ , – т. н. правило трёх сигма (соответствующая вероятность меньше 0,003). Сумма независимых случайных величин $X_1, X_2,…, X_n$, имеющих Н. р. с параметрами $ mathbf EXi=ai, DXi=, i=1,…, n,$ нормально распределена с параметрами $a=a_1+a_2+dots +a_n и sigma^2=sigma^2_{1}+dots+sigma^2_{n}.$
Справедливо и обратное: если сумма $n$ независимых случайных величин нормально распределена, то и каждая из них имеет Н. р., а параметры этих Н. р. связаны указанными равенствами; это следует из одной теоремы, доказанной $Х$. Крамером.
Н. р. встречается в большом числе приложений. Теоретич. обоснование исключит. роли Н. р. дают предельные теоремы теории вероятностей, в частности центральная предельная теорема. Качественно это может быть объяснено следующим образом: Н. р. служит хорошим приближением каждый раз, когда рассматриваемая случайная величина представляет собой сумму большого числа независимых случайных величин, максимальная из которых мала по сравнению со всей суммой.
Н. р. может также появляться как точное решение некоторых задач (в рамках принятой математич. модели явления). Так обстоит дело в теории случайных процессов (в одной из осн. моделей броуновского движения). Классич. примеры возникновения Н. р. как точного принадлежат К. Гауссу (закон распределения ошибок наблюдения) и Дж. К. Максвеллу (закон распределения скоростей молекул).
Совместное распределение нескольких случайных величин $X_1, X_2, …, X_s$ называется многомерным нормальным, если при любых действительных $t_1, t_2, …, t_s $ случайная величина $t_1X_1+t_2X_2+ …+t_sX_s $ имеет Н. р. или равна постоянной. Если она ни при каких $t_1, t_2, …, t_s$ не равна постоянной, то совместное распределение $X_1, X_2, …, X_s $ имеет плотность вида$$p(x_1, x_2, dots, x_s)=Cquad exp big(-sum_{k,l=1}^sq_{k,l}(x_k-a_k)(x_1-a_1)big), $$
где сумма является положительно определённой квадратичной формой, $a_1, a_2, …, a_s$ равны математич. ожиданиям $X_1, X_2, …, X_s$ соответственно, коэффициенты $C$ и $q_{kl}=q_{lk}$ могут быть выражены через дисперсии $X_1, X_2, …, X_s$ и коэффициенты корреляции $ρ_{kl}$ между $X_k$ и $X_l$. Напр., двумерное Н. р. имеет плотность $$p(x,y)=Сquad exp big(-frac{1}{2(1-p^2)}times big[-frac{(x-a_1)^2}{sigma_1^2}+frac{(y-a_2)^2}{sigma_2^2}-frac{2p(x-a_1)(y-a_2)}{sigma_1 sigma_2}big] big),$$где$$C=big(2 pi sigma_1 sigma_2 sqrt {1-p^2}big)^{-1},$$$a_1, a_2$ и $sigma^2_1, sigma^2_2$ – математич. ожидания и дисперсии величин $X$ и $Y, ρ$ – коэф. корреляции между $X$ и $Y$:$$p[=frac{Ἕ[(X-a_1)(Y-a_2)]}{sigma_1 sigma_2}$$
Общее количество параметров, задающих многомерное Н. р., равно $frac{(s+1)(s+2)}{2}-1$
и быстро растёт с увеличением $s$ (равно 20 при $s=5 $ и 65 при $s=10$). Многомерное Н. р. служит осн. моделью многомерного статистич. анализа. Оно используется также в теории случайных процессов (где рассматривают также Н. р. в бесконечномерных пространствах).
О вопросах, связанных с оценкой параметров Н. р. по результатам наблюдений, см. в ст. Несмещённая оценка. Термин «Н. р.» принадлежит К. Пирсону.
Предлагаю вашему вниманию адаптированный перевод главы книги OnlineStatBook посвященной нормальным распределениям.
Вводный раздел определяет, что значит для распределения быть нормальным и представляет некоторые важные свойства нормального распределения. Интересная история открытия нормального распределения описана во втором разделе. Методы вычисления вероятностей, основанные на нормальном распределении, описаны в разделе «Области нормального распределения». «Разновидности нормального распределения» позволяет вам вводить значения среднего и стандартного отклонения нормального распределения и строить графики получившегося распределения. Часто используемое нормальное распределение, называемое стандартным нормальным распределением, описывается в одноименном разделе. Биномиальное распределение может быть аппроксимировано нормальным. Раздел «Нормальное приближение к биномиальному распределению» показывает это приближение. Демонстрация аппроксимации нормальным распределением позволяет вам исследовать точность этого приближения.
Введение
Нормальное распределение является наиболее важным и широко используемым распределением в статистике. Его иногда называют «колоколообразной кривой», хотя музыкальные качества такого колокола были бы не так приятны. Также его называют «распределением Гаусса» в честь математика Карла Фридриха Гаусса. Как вы увидите в разделе об истории нормального распределения, хотя Гаусс играл в ней важную роль, впервые обнаружил нормальное распределение Абрахам де Муавр.
Строго говоря, некорректно говорить о «нормальном распределении» поскольку существует много нормальных распределений. Нормальные распределения могут отличаться своими средними и стандартными отклонениями. На рис. 1 три нормальных распределения. У зеленого (самого левого) среднее равно -3, а стандартное отклонение 0.5, у красного распределения (посередине) среднее равно 0, а стандартное отклонение 1, и у черного распределение (справа) среднее равно 2 а стандартное отклонение 3. Эти, как и все другие нормальные распределения являются симметричными с относительно большими значениями в центре распределения и меньшими значениями в хвостах.

Плотность нормального распределения (высота для данного значения на оси x) показана ниже. Нормальное распределение определяется параметрами (mu) и (sigma) являющимися средним и стандартным отклонением соответственно. Символ (e) это основание натурального логарифма, а (pi) это константа пи.
$$
frac{1}{sqrt{2pisigma^2}} e^{frac{-(x-mu)^2}{2sigma^2}}
$$
Поскольку мы не будем углубляться в математическую трактовку статистики, не беспокойтесь, если это выражение вас смущает. Мы не будем возвращаться к нему в следующих разделах.
Семь свойств нормального распределения указаны ниже. Эти свойства будут более подробно проиллюстрированы в следующих разделах этой главы.
- Нормальные распределения симметричны относительно своих средних.
- Среднее значение, мода и медиана нормального распределения совпадают.
- Площадь под нормальным распределением равна 1.
- Нормальные распределения плотнее в центре и менее плотны в хвостах.
- Нормальные распределения определяются двумя параметрами: среднее (m) и стандартное отклонение (s).
- 68% площади нормального распределения находится в пределах одного стандартного отклонения от среднего.
- Примерно 95% площади нормального распределения находится в пределах двух стандартных отклонений от среднего.
История нормального распределения
В главе посвященной вероятности мы увидели, что биномиальное распределение можно использовать для таких проблем, как: «Если подбросить честную монету 100 раз, какова вероятность выпадения 60 и более орлов?» Вероятность выпадения ровно x орлов за N подбрасываний рассчитывается по формуле:
$$
P(X) = frac{N!}{x!(N-x!)}p^x(1-p)^{N-x}
$$
Где (x) это число орлов (60), (N) – количество подбрасываний монеты (100), а (p) это вероятность выпадения орла (0.5). Таким образом, чтобы решить эту проблему вам нужно вычислить вероятность 60 орлов, затем вероятность 61 орла, 62 и т.д. и сложить эти вероятности. Представьте, сколько времени потребовалось бы для вычисления биномиальных вероятностей до появления калькуляторов и компьютеров.
Абрахам де Муавр, статистик 18-го века и консультант азартных игроков, часто привлекался к проведению этих длительных вычислений. Де Муавр заметил, что, когда число событий (подбрасываний монет) увеличивается, форма биномиального распределения приближается к очень плавной кривой. Биномиальное распределение для 2, 4 и 12 подбрасываний показаны на рис. 2.

Де Муавр рассуждал, что, если бы он мог найти математическое выражение для этой кривой, он мог бы гораздо легче решать такие проблемы, как нахождение вероятности 60 и более орлов из 100 бросков монет. В точности это он и сделал, и кривая, которую он открыл, теперь называется «нормальной кривой».

Важность нормальной кривой обусловлена тем, что распределения многих природных явлений, по крайней мере приблизительно, нормально распределены. Одно из первых применений нормального распределения было к анализу ошибок измерений, сделанных при астрономических наблюдениях, ошибок произошедших из-за несовершенства инструментов и наблюдателей. Галилео в 17 веке отметил, что эти ошибки были симметричными и что небольшие ошибки возникали чаще, чем большие. Это привело к нескольким гипотезам о распределении ошибок, но только в начале 19-го века было установлено, что эти ошибки соответствуют нормальному распределению. Независимо друг от друга математики Адрейн в 1808 г. и Гаусс в 1809 г. разработали формулу для нормального распределения и показали, что ошибки хорошо соответствуют этому распределению.
Это же распределение было обнаружено Лапласом в 1778 г., когда он вывел чрезвычайно важную центральную предельную теорему, тему одного из следующих разделов. Лаплас показал, что даже если распределение не является нормальным, средние повторяющихся выборок из распределения будут распределены почти нормально, и чем больше размер выборки, тем ближе к нормальному будет распределение средних.
Большинство статистических процедур для проверки между средними значениями предполагают нормальное распределение. Поскольку распределение средних близко к нормальному, эти тесты работают хорошо даже если само распределение только приблизительно нормально. Кетле был первым, кто применил нормальное распределение к человеческим характеристикам. Он отметил, что такие характеристики, как рост, вес и сила были нормально распределены.
Площади нормального распределения
Площади под кусками нормального распределения могут быть вычислены с использованием математического анализа. Поскольку это нематематический подход к статистике, мы будем полагаться на компьютерные программы и таблицы для определения этих областей. На рис. 4 показано нормальное распределение со средним значением 50 и стандартным отклонением 10. Затененная область между 40 и 60 содержит 68% распределения.

На рис. 5 изображено нормальное распределение со средним равным 100 и стандартным отклонением 20. Как и на рис. 4, 68% распределения лежит в пределах одного стандартного отклонения от среднего.

Нормальные распределения показанные на рис. 4 и 5 это частные случаи общего правила о том, что 68% площади любого стандартного распределения находится в пределах одного стандартного отклонения от среднего.
На рис. 6 изображено нормальное распределение со средним 75 и стандартным отклонением 10. Закрашенная область содержит 95% площади и находится между 55.4 и 94.6. Для всех нормальных распределений 95% площади находится в пределах 1.96 стандартного отклонения. Для быстрых приближений иногда полезно округлять и использовать 2 вместо 1.96, в качестве числа стандартных отклонений, на которые вам нужно отступить от среднего, чтобы охватить 95% площади.

Для вычисления площадей под нормальным распределением может быть использован следующий нормальный калькулятор. Например, вы можете использовать его, чтобы найти пропорцию части нормального распределения со средним 90 и стандартным отклонением 12, которая больше 100. Установите среднее равным 90, стандартное отклонение – 12. Затем введите 110 в ячейку справа от кнопки «Above». Внизу экрана вы увидите, что закрашенная область равна 0.0478. Посмотрите сможете ли вы использовать калькулятор, чтобы узнать, что площадь между 115 и 120 равна 0.0124.

Скажем, вы хотите найти оценку, соответствующую 75-му перцентилю нормального распределения со средним значением 90 и стандартным отклонением 12. Используя обратный нормальный калькулятор, введите параметры, как показано на рис. 8, и обнаружьте, что площадь ниже 98.09 равна 0.75.

Стандартное нормальное распределение
Как обсуждалось во вводном разделе, у нормальных распределений не обязательно одинаковые средние и стандартные отклонения. Нормальное распределение со средним равным 0 и стандартным отклонением 1 называется стандартным нормальным распределением.
Области нормального распределения часто представлены таблицами стандартного нормального распределения. Часть таблицы стандартного нормального распределения показана в таблице 9.
| Z | Площадь под |
| -2.5 | 0.0062 |
| -2.49 | 0.0064 |
| -2.48 | 0.0066 |
| -2.47 | 0.0068 |
| -2.46 | 0.0069 |
| -2.45 | 0.0071 |
| -2.44 | 0.0073 |
| -2.43 | 0.0075 |
| -2.42 | 0.0078 |
| -2.41 | 0.008 |
| -2.4 | 0.0082 |
| -2.39 | 0.0084 |
| -2.38 | 0.0087 |
| -2.37 | 0.0089 |
| -2.36 | 0.0091 |
| -2.35 | 0.0094 |
| -2.34 | 0.0096 |
| -2.33 | 0.0099 |
| -2.32 | 0.0102 |
Первый столбец «Z» содержит значения стандартного нормального отклонения; второй столбец показывает значение площади левее Z. Поскольку среднее распределения равно нулю, а стандартное отклонение 1, в столбец Z равен числу стандартных отклонений левее (или правее) среднего значения. Например, Z равное -2.5 представляет значение равное 2.5 стандартных отклонений левее среднего. Площадь левее Z равна 0.0062.
Ту же информацию можно получить с помощью следующего калькулятора. На рис. 10 показано, как его можно использовать для вычисления площади левее значения -2,5 для стандартного нормального распределения. Обратите внимание, что среднее значение установлено на 0, а стандартное отклонение установлено на 1.

Значение из любого нормального распределения может быть преобразовано в соответствующее значение в стандартном нормальном распределении при помощи следующей формулы:
$$
Z = frac{(X-mu)}{sigma}
$$
где (Z) это значение стандартного нормального распределения, (X) – значение исходного распределения, (mu) — среднее исходного распределения, а (sigma) — стандартное отклонение исходного распределения.
В качестве простого упражнения, какая часть нормального распределения со средним значением 50 и стандартным отклонением 10 меньше 26? Применяя формулу, получаем:
$$
Z = (26 – 50)/10 = -2.4
$$
Из таблицы 9, мы знаем, что 0.0082 распределения левее -2.4. Нет необходимости преобразовывать значение к (Z) если вы используете апплет как показано на рис. 11.

Если все значения распределения преобразовать в (Z) значения, то у распределения будет среднее 0 и стандартное отклонение 1. Процесс преобразования распределения к стандартному со средним 0 и отклонением 1 называется стандартизацией распределения.
Приближение биномиального распределения нормальным
В разделе об истории нормального распределения мы видели, что нормальное распределение можно использовать для аппроксимации биномиального распределения. В этом разделе показывается, как рассчитать эти приближения.
Давайте начнем с примера. Пусть у вас есть честная монета, и вы хотите знать вероятность выпадения 8 орлов за 10 бросков. У биномиального распределения есть среднее равное
(mu = Np = 10*0.5 = 5) и дисперсия (sigma^2 = Np(1-p) = 10*0.5*05 = 2.5). Стандартное отклонение при этом равно 1.5811. Результат 8 орлов равен ((8 — 5)/1.5811 = 1.897) стандартных отклонений правее среднего распределения. «Какова вероятность получения значения в точности равного 1.897 стандартных отклонений правее среднего?» Вы можете удивиться, но ответ равен 0. Вероятность любой отдельной точки равна 0. Проблема в том, что биномиальное распределение является дискретным вероятностным распределением, тогда как нормальное распределение непрерывно.
Решение состоит в том, чтобы округлить и рассмотреть все значения от 7.5 до 8.5, для получения результат 8 орлов. Используя этот подход, мы вычисляем площадь под нормальной кривой от 7.5 до 8.5. Зона зеленого цвета на рис. 12 является приблизительной вероятностью получения 8 орлов.

Решение состоит в том, чтобы вычислить эту площадь. Сначала мы вычисляем площадь левее 8.5, а затем вычитаем из нее площадь левее 7,5.
Результаты использования калькулятора площади нормального распределения для определения области ниже 8.5 показаны на рисунке 13. Результаты для 7.5 показаны на рисунке 14.


Разница между площадями составляет 0.044, что является приближением биномиальной вероятности. Для этих параметров приближение очень точное.
Если у вас не было калькулятора площади нормального распределения, вы могли бы найти решение с помощью таблицы стандартного нормального распределения (таблица 9) следующим образом:
- Найти значение (Z) для 8.5, используя формулу (Z = (8.5 — 5) / 1.5811 = 2.21).
- Найти площадь левее (Z) равного 2.21 (= 0,987).
- Найти значение (Z) для 7.5, используя формулу (Z = (7.5 — 5) / 1,5811 = 1.58).
- Найти площадь левее (Z) 1.58 (= 0.943).
- Вычесть значение на шаге 4 из значения на шаге 2, и получить 0.044.
Та же логика применяется при расчете вероятности диапазона результатов. Например, чтобы рассчитать вероятность от 8 до 10 подбрасываний, вычислите площадь от 7.5 до 10.5.
Точность аппроксимации зависит от значений (N) и (p). Эмпирическое правило заключается в том, что аппроксимация хороша, если оба значения (Np) и (N (1-p)) больше 10.
Статистическая грамотность
Анализ рисков часто основан на предположении о нормальном распределении. Критики говорят, что экстремальные явления в действительности происходят чаще, чем можно было бы ожидать, если бы они были нормальными. Предположение даже было названо «большим интеллектуальным мошенничеством».
Недавняя статья, в которой обсуждается, как защитить инвестиции от экстремальных явлений, названных «риск хвоста» и определяемых как «риск хвоста, или экстремальный шок для финансовых рынков, технически определяется как инвестиция, которая двигается на более трех стандартных отклонений от среднего значения нормального распределения возврата инвестиций.»
Риск хвоста можно оценить, предполагая нормальность распределение и вычисляя вероятность такого события. Так ли следует оценивать «риск хвоста»?
События более трех стандартных отклонений от среднего значения очень редки для нормальных распределений. Однако они не так редки для других распределений, например с сильным перекосом. Если нормальное распределение используется для оценки вероятности событий хвоста, определенных таким образом, то «риск хвоста» будет недооценен.

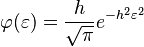
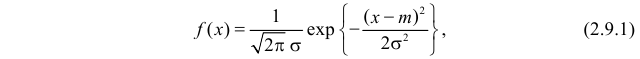
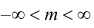
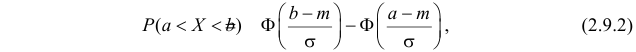
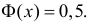
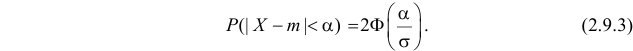
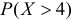
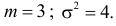
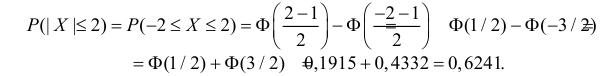
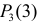
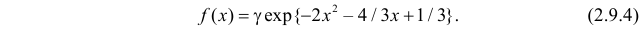
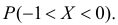
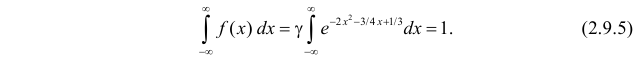
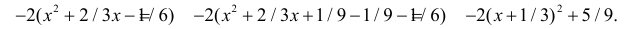
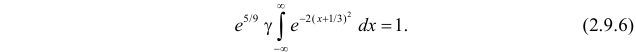

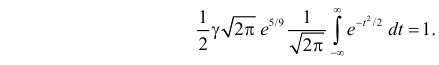

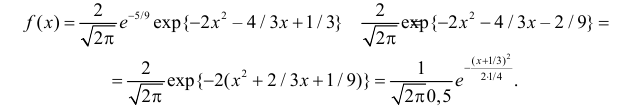
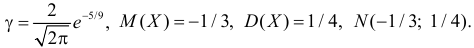
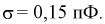
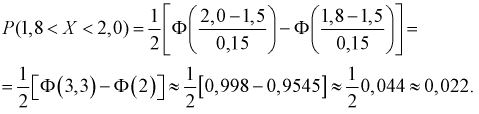
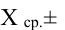
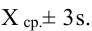
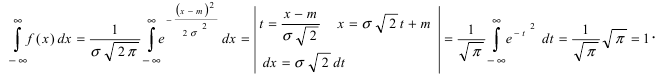
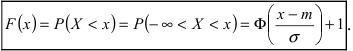
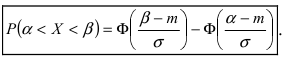
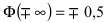 — график функции Лапласа имеет горизонтальные асимптоты
— график функции Лапласа имеет горизонтальные асимптоты