Знак относительной ошибки

УТВЕРЖДАЮ

Зам. директора

НПО «ВНИИМ им. Д.И.
Менделеева»

________________________________

В.С. Александров

«29» декабря 1992 г.

ГОССТАНДАРТ РОССИИ

НПО «ВНИИМ им. Д.И.
Менделеева»

РЕКОМЕНДАЦИЯ

Государственная система обеспечения единства
измерений

Погрешности
измерений. Обозначения

МИ 2246-93

С.-Петербург

1992 г.

РЕКОМЕНДАЦИЯ

ГСИ. Погрешности измерений. Обозначения

МИ 2246-93

Рекомендация распространяется на нормативную
документацию (далее — НД) и устанавливает обозначения погрешностей измерений
величин.

1. ОБЩИЕ ПОЛОЖЕНИЯ

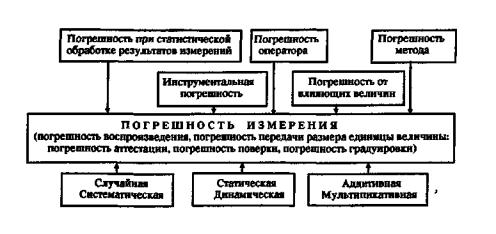
1.1 Погрешность измерений — отклонение
результата измерений от действительного значения измеряемой величины — может
состоять из инструментальной погрешности, погрешности метода, погрешности
оператора и др. погрешностей. Погрешность измерений и ее составляющие
представлены на схеме в приложении 1.

1.2 Погрешность измерений при воспроизведении
единицы величины называют погрешностью воспроизведения единицы, а при передаче
размера единицы величины называют погрешностью передачи размера единицы
величины или погрешностью поверки (погрешностью аттестации).

1.3 Погрешности измерений подразделяют:

в зависимости от характера проявления на
систематические, случайные;

в зависимости от характера их изменения в
диапазоне измеряемой величины на аддитивные и мультипликативные;

по форме представления на абсолютные и
относительные.

1.4 Погрешность измерений может быть
выражена в виде:

доверительного интервала;

пределов допускаемой погрешности;

характеристик распределения погрешностей (среднее
квадратическое отклонение результата измерений, размах, среднее арифметическое
и др. характеристики).

Примечание. Задаваемые или
допускаемые характеристики погрешностей измерений могут быть выражены в
соответствии с требованиями, установленными в МИ
1317, в форме:

предела допускаемых значений
характеристики;

нижнего и
верхнего пределов допускаемых значений характеристики.

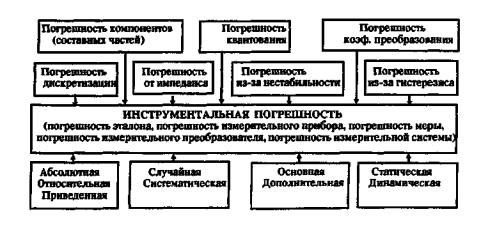
1.5 Наибольший вклад в погрешность
измерений, как правило, вносит инструментальная погрешность, обусловленная
погрешностью применяемого средства измерений (далее — СИ). Инструментальная
погрешность и ее составляющие приведены в приложении 2.

2. ОБОЗНАЧЕНИЯ ПОГРЕШНОСТЕЙ

2.1 Для обозначения какой-либо
погрешности используют букву греческого алфавита «дельта» — Δ
(прописная), δ (строчная).

Прописной буквой Δ обозначают
абсолютную погрешность измерения и строчной буквой δ — относительную
погрешность измерения.

2.2 Неисключенную систематическую
погрешность измерения рекомендуется обозначать буквой греческого алфавита
«тэта» — Θ.

2.3. Среднее квадратическое отклонение и
размах — характеристики случайной погрешности — рекомендуется обозначать
буквами латинского алфавита S и R соответственно.

2.4. Поправку, которую вводят в неисправленный
результат измерения с целью исключения одной или нескольких систематических погрешностей,
обозначают символом Ñ
(перевернутой буквой греческого алфавита «дельта»).

2.5 Метрологические характеристики СИ —
нестабильность и вариацию — рекомендуется обозначать буквой греческого v
(ню) и латинского V алфавитов соответственно.

3. ИНДЕКСАЦИЯ СИМВОЛОВ

3.1 При необходимости конкретизации
погрешности измерения (указания ее составляющей, формы представления или
внесения других уточняющих данных) рекомендуется символ погрешности
сопровождать индексом (индексами).

3.2 В качестве индексов используют первую
букву или несколько букв того слова, которое определяет или источник
погрешности, или форму представления ее, или другие особенности погрешности.

3.3 Для индексации рекомендуется
применять буквы русского, латинского и греческого алфавитов (например, Δ_Σ
— суммарная погрешность результата измерений). Индексы пишутся как прописными,
так и строчными буквами.

3.4 При необходимости указания величины,
погрешность которой оценивается, в качестве индекса рекомендуется использовать
символ этой величины (например, Δ _L , — абсолютная погрешность измерений длины, δ _м — относительная погрешность
измерений массы и т.д.).

Обозначения (символы) наиболее
распространенных величин представлены в приложении 3.

Примечание. Если в тексте измеряемую величину обозначают
символом х, у и т.д., то и погрешность измерений этих величин
обозначают соответственно Δ_х или δ_х Δ_у
или δ_у и т.д.

3.5 Дополнительную погрешность средств
измерений, возникающую вследствие изменения показаний последних из-за
воздействия влияющих величин, обозначают либо Δ_доп
(дополнительная абсолютная погрешность СИ), либо δ_доп
(дополнительная относительная погрешность СИ).

Дополнительную погрешность результата измерений,
возникающую вследствие воздействия влияющих величин на измеряемую величину,
обозначают либо Δ _вв,
либо δ _вв.

3.6. В приложении
4 дан перечень допускаемых сокращений слов, применяемых в метрологической
практике для указания источника погрешности (составляющих погрешности
измерений).

3.7. Для индексации символов при
обозначении погрешности средств измерений рекомендуется использовать
аббревиатуру, уточняющую вид средства измерений (например, Δ _си — абсолютная погрешность средства измерений, δ _иис — относительная погрешность
измерительной информационной системы и т.д.).

В приложении 5
приведена аббревиатура для обозначения некоторых средств измерений.

4. СТРУКТУРА ИНДЕКСАЦИИ

4.1 При необходимости указания нескольких
индексов у одного символа сначала указывается индекс, характеризующий источник
погрешности (составляющую погрешности), а потом — индекс, характеризующий форму
ее представления (например, предел допускаемой погрешности метода, заданной в
абсолютной форме, должен быть выражен как Δ_{м, пр} ).

4.2. Если наличие нескольких индексов у
одного символа приводит к затруднению их раздельного прочтения, их разделяют
запятой (например, Δ_о,
пр предел допускаемой основной
погрешности средства измерений в абсолютной форме, Δ _{дин, макс}
— максимальное значение динамической погрешности средства измерений в
относительной форме).

4.3. Допустимо применять символы погрешностей,
опуская некоторые индексы, если это не приводит к затруднению понимания текста
(например, если речь идет о конкретном средстве измерений, то индекс в виде
аббревиатуры, конкретизирующий средство измерений, можно опускать. Если в НД
речь идет об измерениях конкретной величины и ее погрешности измерений, то
индекс, конкретизирующий измеряемую величину, можно опустить. Наличие индексов «о»
(основная), «доп» (дополнительная), «прв» (приведенная)
снимает необходимость дополнительного указания индекса «СИ».

4.4. Для пояснения того, характеристику
какой погрешности представляет среднее квадратическое отклонение » S «, рекомендуется сразу после символа «S»
указывать в круглых скобках эту погрешность (например, S ( Δ _дон ) —
среднее квадратическое отклонение дополнительной погрешности средства
измерений). Среднее квадратическое отклонение единичного результата измерений
рекомендуется обозначать только символом «S«. При обозначении
среднего квадратического отклонения результата многократных измерений (среднего
арифметического) сразу после символа «S» в круглых скобках
указывают символ результата измерений (например, S( ) — среднее квадратическое отклонение среднего
арифметического группы экспериментальных данных).

4.5. При указании нестабильности «v»
метрологической характеристики последнюю указывают в круглых скобках после
символа нестабильности (например, v ( Δ _сист ) нестабильность систематической погрешности).

Время, в течение которого фиксируется
нестабильность, чаще всего указывается в тексте документа или в техническом
тексте. При необходимости указания времени нестабильности в обозначении, оно
указывается символом «τ» в качестве индекса к символу
нестабильности v (например, v_τ ( Δ _сист )
— нестабильность систематической погрешности за время τ).

4.6 Доверительную погрешность
рекомендуется обозначать соответствующим символом погрешности с указанием
вероятности в круглых скобках после символа этой погрешности (например, Δ (0,95) — абсолютная доверительная погрешность
измерений при вероятности Р = 0,95).

4.7 Структура
обозначений наиболее часто употребляемых погрешностей приведена в виде примера
ниже:

доверительная погрешность результата измерений длины стержня	Δ L (Р)
дополнительная погрешность средства измерений, вызванная изменением температуры окружающей среды, выраженная в относительной форме	δ СИ , д on , t или δ доп , t
дополнительная погрешность результата измерений, возникающая из-за воздействия магнитной индукции на измеряемую величину	Δ Ф
неисключенная систематическая погрешность метода при измерениях массы	Θм,М
нестабильность систематической погрешности средства измерений за время Т	v τ (ΔСИ,сист) или vτ( Δ сист )
предел допускаемого значения среднего квадратического отклонения случайной погрешности средства измерений	S пр (ΔСИ,сист)
приведенная погрешность средства измерений	δ СИ , прв или δ прв
среднее квадратическое отклонение единичного измерения	S
среднее квадратическое отклонение результата измерений (среднего арифметического)	S ( ) или S ( )
среднее квадратическое отклонение неисключенной систематической погрешности.	S ( Θ )

Приложение 1

Погрешность измерения и ее составляющие*

* Примечание.
На рисунке приведены в качестве примеров возможные составляющие погрешности измерения
для лучшего понимания принципов индексации.

Приложение 2

Инструментальная погрешность и ее составляющие*

* Примечание.
На рисунке приведены в качестве примеров возможные составляющие инструментальной
погрешности для лучшего понимания принципов индексации.

Приложение 3

Обозначения (символы) наиболее распространенных
величин

Наименование физической величины	Обозначение
Длина	L
Масса	М
Время	t
Температура	T , t
Сила электрического тока	I
Сила света	J
Угол (плоский)	j
Частота	f
Сила, вес	F
Энергия	W
Количество электричества	Q
Электрическое напряжение	U
Электрическая емкость	с
Электрическое сопротивление	R
Поток магнитной индукции	Ф
Скорость	v
Ускорение	a
Длина волны	l
Плотность	r

Приложение 4

Перечень допускаемых сокращений слов, используемых
в качестве индекса для метрологической практики

Полное наименование	Сокращение
аддитивная	адд
аппаратура	ап
аттестация	ат
влияющая величина	ВВ
воспроизведение	всп
градуировка	гр
динамическая	дин
дополнительная	доп
запаздывание	зпд
инструментальная	и
интерполяция	инт
максимальная	макс
мера	мер
метод	м
минимальная	мин
мультипликативная	мл
округление	ок
оператор	оп
основная	о
отсчитывание	отс
параллакс	пар
передача	пер
поверка	пов
предел	пр
приведенная	прв
случайная	c л
систематическая	сист
средство измерений	СИ
стандартный образец	СО
статическая	ст
теоретическая	т
частная	ч

Примечание. Предлагаемые сокращения не всегда совпадают с
правилами сокращений в русском языке, но авторы ориентировались на краткость
сокращений с целью удобства индексации.

Приложение 5

Аббревиатура для обозначений некоторых средств
измерений

Средство измерений	Аббревиатура
Вспомогательное средство измерений	ВСИ
Измерительно-вычислительный комплекс	ИВК
Измерительный канал	ИК
Измерительная информационная система	ИИС
Измерительный преобразователь	ИП
Измерительный прибор	ИПр
Измерительная система	ИС
Измерительная установка	ИУ
Рабочее средство измерений	РСИ
Средство измерений	СИ
Цифровой измерительный прибор	ЦПр

Содержание

Измерение
— экспериментальное сравнение, данной
величины с другой, такого же рода
величиной, принятой за единицу меры.

Задачей
измерения является:

1)
получение приблизительного значения
измеряемой величины;

2)
оценка величины погрешности.

Измерения
могут быть прямыми
и косвенными.

Прямое
измерение
непосредственное сравнение измеряемой
величины с единицей измерения с помощью
приборов и устройств, проградуированных
в соответствующих единицах (измерение
линейных размеров линейкой, штангенциркулем;
измерение времени секундомером;
взвешивание и т.п.)

Косвенно
измеряемая величина
рассчитывается с помощью некоторой
зависимости (формулы) от других величин,
полученных прямыми измерениями
(определение скорости v=s / t по пути и
времени, плотности ρ= m / v по массе и
объему и т.д.).

Любое
измерение не дает абсолютно точного
значения измеряемой величины – неточность
приборов, влияние внешних факторов,
трение и т.д., –поэтому измеренные
значения всегда отклоняются от истинного.
Эти отклонения называются ошибками
или погрешностями
измерений.

Источниками
погрешности являются: несовершенство
применяемых методов и средств измерений,
непостоянство влияющих на результат
измерения физических величин, а также
индивидуальные особенности экспериментатора.
Кроме того, на точность измерений влияют
внешние и внутренние помехи, климатические
условия и порог чувствительности
измерительного прибора.

Истинное
значение физической величины —
это значение, идеальным образом отражающее
свойство данного объекта, как в
качественном, так и в количественном
отношении. Оно не зависит от средств
нашего познания и является той абсолютной
истиной, к которой мы стремимся, пытаясь
выразить ее в виде числовых значений.

На
практике это абстрактное понятие
приходится заменять понятием
«действительное значение».

Действительное
значение физической величины
— значение, найденное экспериментально
и настолько приближающееся к истинному,
что для данной цели может быть использовано
вместо него.

Результат
измерения представляет
собой приближенную оценку истинного
значения величины, найденную путем
измерения.

Точность
измерений
отражает меру близости результатов
измерений к истинному значению измеряемой
физической величины. Высокой точности
измерений соответствует малая погрешность.

Так,
например, измерение силы тока в 10А и
100А может быть выполнено с идентичной
абсолютной погрешностью Δ = +1А.

Погрешность
результата измерения —
это разница между результатом измерения
и истинным (действительным) значением
измеряемой величины.

Погрешность
средства измерения —
разность между показаниями средства
измерения и истинным (действительным)
значением измеряемой физической
величины. Она характеризует точность
результатов измерений, проводимых
данным средством.

Эти
два понятия во многом близки друг к
другу и классифицируются по одинаковым
признакам.

Классификация
погрешностей

• В
  зависимости от формы выражения
  различают абсолютную, относительную
  и приведенную погрешности.

Абсолютной
погрешностью Δ,
выражаемой в единицах измеряемой
величины, называется отклонение
результата измерения х от истинного
значения х_и:

Δ
= х — х_и

Абсолютная
погрешность характеризует величину и
знак полученной погрешности, но не
определяет качество самого проведенного
измерения.

Понятие
погрешности характеризует как бы
несовершенство измерения. Качество
(точность) первого измерения ниже
второго. Поэтому, чтобы иметь возможность
сравнивать качество измерений, введено
понятие относительной погрешности.

Относительной
погрешностью δ
называется отношение абсолютной
погрешности измерения к истинному
значению измеряемой величины:

Мерой
точности измерений служит показатель,
обратный модулю относительной погрешности:

Относительную
погрешность δ часто выражают в процентах:

Приведенная
погрешность γ
— это отношение абсолютной погрешности
Δ к некоторому нормирующему значению
X_N
(например, к конечному значению шкалы
прибора или сумме значений шкал при
двусторонней шкале):

где
X_n —
нормирующее значение, которое зависит
от типа шкалы измерительного прибора
и определяется по его градуировке:

— если
шкала прибора односторонняя, то есть
нижний предел измерений равен нулю, то
X_n
определяется равным верхнему пределу
измерений;

— если
шкала прибора двухсторонняя, то
нормирующее значение равно ширине
диапазона измерений прибора.

Приведённая
погрешность является безразмерной
величиной, либо измеряется в процентах.

• По
  характеру (закономерности) проявления
  погрешности
  делятся на систематические, случайные
  и грубые (промахи).

Систематическая
погрешность
Δ_с
— составляющая погрешности измерения,
остающаяся постоянной или закономерно
меняющаяся при повторных измерениях
одной и той же физической величины.

Величина
систематической погрешности Δ_с
характеризует один из показателей
качества измерений — правильность
полученного результата, чем меньше
величина Δ_с,
тем правильнее полученный результат.

Систематическая
ошибка может быть обусловлена
неисправностью прибора, несовершенством
методики измерений (например неучетом
сил трения) и т.д

Такие
погрешности могут быть выявлены путем
детального анализа возможных их
источников и уменьшены введением
соответствующей поправки, применением
более точных приборов, калибровкой
приборов с помощью рабочих мер и пр.
Однако полностью их устранить нельзя.

Случайная
погрешность
— изменяющаяся случайным
образом по знаку и значению при повторных
измерениях одной и той же величины в
одних и тех же условиях.

Случайные
погрешности могут быть связаны с
несовершенством приборов (трение в
механических приборах и т. п.),
тряской в городских условиях, с
несовершенством объекта измерений
(например, при измерении диаметра тонкой
проволоки, которая может иметь не совсем
круглое сечение в результате несовершенства
процесса изготовления), с особенностями
самой измеряемой величины (например
при измерении количества элементарных
частиц, проходящих в минуту через счётчик
Гейгера).

Величина
случайной погрешности
характеризует другой
показатель качества измерений — сходимость
результатов при повторных измерениях
одного и того же значения измеряемой
физической величины.

В
отличие от систематических погрешностей
случайные погрешности нельзя исключить
из результатов измерений путем введения
поправки, однако, их можно существенно
уменьшить путем многократного измерения
этой величины и последующей статистической
обработкой полученных результатов.

Грубая
погрешность (промах)
— это случайная погрешность результата
отдельного наблюдения, входящего в ряд
измерений, которая для данных условий
резко отличается от остальных результатов
этого ряда.

Данные
погрешности возникают из-за ошибок
оператора или неучтенных внешних
воздействий.

• По
  причинам возникновения (по виду
  источника)

1
Инструментальные
погрешности
возникают
из-за несовершенства средств измерения,
т.е. от погрешностей средств измерений.
Иногда эту погрешность называют
аппаратурной.

Источниками
инструментальных погрешностей могут
быть, например, неточная градуировка
прибора и смещение нуля, вариация
показаний прибора в процессе эксплуатации
и т.д. Уменьшают инструментальные
погрешности применением более точного
прибора.

2
Внешняя погрешность —
важная составляющая погрешности
измерения, связанная с отклонением
одной или нескольких влияющих величин
от нормальных значений или выходом их
за пределы нормальной области (например,
влияние влажности, температуры, внешних
электрических и магнитных полей,
нестабильности источников питания,
механических воздействий и т.д.).

В
большинстве случаев внешние погрешности
являются систематическими и определяются
дополнительными погрешностями применяемых
средств измерений.

3
Методическая погрешность
обусловлена несовершенством метода
измерений, влиянием выбранного средства
измерений на измеряемые параметры
сигналов, некорректностью алгоритмов
или расчетных формул, по которым
производят вычисления, округления
результатов, отличием принятой модели
объекта измерений от той, которая
правильно описывает его свойство,
определяемое путем измерения.

Отличительной
особенностью методических погрешностей
является то, что они не могут быть указаны
в нормативно-технической документации
на используемое средство измерений,
поскольку от него не зависят, а должны
определяться оператором в каждом
конкретном случае. В связи с этим оператор
должен четко различать фактически
измеренную им величину и величину,
подлежащую измерению.

Если,
например, вольтметр имеет недостаточно
высокое входное сопротивление, то его
подключение к схеме способно изменить
в ней распределение токов и напряжений.
При этом результат измерения будет
отличаться от действительного.

Пример
1

Рассмотрим
появление методической погрешности
при измерении сопротивления методом
вольтметра-амперметра (рисунок 8).

Рисунок
8- К появлению методической погрешности

Для
определения значения сопротивления R_x
резистора необходимо измерить ток I_R,
протекающий через резистор и падение
напряжения на нем U_R.
В приведенной схеме, реализующей этот
метод, падение напряжения на резисторе
измеряется вольтметром непосредственно,
в то время как амперметр измеряет
суммарный ток, часть которого протекает
через резистор, часть через вольтметр.
В результате измеренное значение
сопротивления будет не R_x
= U_R
/ I_R,
а R’ = U_R
/ (I_R
+ I_v)
и появляется методическая погрешность
измерения ΔR = R’ — R_x
. Методическая погрешность уменьшается
и стремится к нулю при токе I_v
→ 0, т.е. при внутреннем сопротивлении
вольтметра R_v
→ ∞.

Методическую
погрешность можно уменьшить путем
применения более точного метода
измерения.

4
Субъективные (личные) погрешности
вызываются ошибками оператора при
отсчете показаний средств измерения
(погрешности от небрежности и невнимания
оператора, от параллакса, т.е. от
неправильного направления взгляда при
отсчете показаний стрелочного прибора
и пр.).

Подобные
погрешности устраняются применением
современных цифровых приборов или
автоматических методов измерения.

• В
  зависимости от влияния характера
  изменения измеряемых величин
  погрешности
  средств измерений делят на статические
  и динамические.

Статическая
погрешность
— это погрешность средств измерений
применяемого для измерения физической
величины, принимаемой за неизменную.

Динамической
называют
погрешность средств измерений, возникающая
дополнительно при измерении переменной
физической величины и обусловленная
несоответствием его реакции на скорость
(частоту) изменения измеряемого сигнала.

• По
  условиям, в которых используются
  средства измерения,
  различают основную и дополнительную
  погрешности.

Основная
погрешность
измерений — та погрешность, которая
имеет место при нормальных условиях
его эксплуатации, оговоренных в
регламентирующих документах (паспорте,
технических условиях и пр.)

Дополнительная
погрешность
средства измерения возникает вследствие
выхода какой-либо из влияющих величин
(температуры, влажности и др.) за пределы
нормальной области значений.

Пример
3

Вольтметр
предназначен для измерения переменного
тока с номинальным значением частоты
(50 ± 5)Гц. Отклонение частоты за эти
пределы приведет к дополнительной
погрешности измерения.

• По
  зависимости абсолютной погрешности
  от значений измеряемой величины
  различают
  погрешности (рисунок 9):

• аддитивные
  Δ_а
  , не зависящие от измеряемой величины;

• мультипликативные
  Δ_м
  , которые прямо пропорциональны
  измеряемой величине;

• нелинейные
  Δ_н
  , имеющие нелинейную зависимость от
  измеряемой величины.

Рисунок
9 — Аддитивная (а), мультипликативная
(б), нелинейная (в) погрешности

Эти
погрешности применяют в основном для
описания метрологических характеристик
средств измерений.

Примеры
аддитивных погрешностей — от постоянного
груза на чашке весов, от неточной
установки на нуль стрелки прибора перед
измерением, от термо-ЭДС в цепях
постоянного тока.

Причинами
возникновения мультипликативных
погрешностей могут быть: изменение
коэффициента усиления усилителя,
изменение жесткости мембраны или пружины
прибора, изменение опорного напряжения
в цифровом вольтметре.

Заканчивая
анализ классификации погрешностей
измерений, необходимo отметить, что она
(как и любая другая классификация) носит
досрочно условный (относительный)
характер.

Ответы
на вопросы, об отнесении погрешности
конкретного измерения к тем или иным
классам и о делении их на случайные и
систематические, могут бытъ даны лишь
при наличии полной информации о свойствах
параметров характеристик измеряемого
объекта, измерительных устройств,
условий, в которых проводились измерения,
а также, как правило, только после
проведения многочисленных повторных
измерений.

Наглядным
примером может служить климатическая
погрешность измерительного прибора.
Если возможен контроль температуры,
при которой проводятся измерения, и
имеется поправочная таблица, то такую
погрешность следует рассматривать как
систематическую. Однако при отсутствии
контроля температур эта же погрешность
учитывается как случайная.

Обобщённой
характеристикой средств измерения
является класс точности, определяемый
предельными значениями допускаемых
основной и дополнительной погрешностей,
а также другими параметрами, влияющими
на точность средств измерения; значение
параметров установлено стандартами на
отдельные виды средств измерений. Класс
точности средств измерений характеризует
их точностные свойства, но не является
непосредственным показателем точности
измерений, выполняемых с помощью этих
средств, так как точность зависит также
от метода измерений и условий их
выполнения. Измерительным приборам,
пределы допускаемой основной погрешности
которых заданы в виде приведённых
основных (относительных) погрешностей,
присваивают классы точности, выбираемые
из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0;
4,0; 5,0; 6,0)*10ⁿ,
где показатель степени n = 1; 0; −1; −2
и т. д.

Диапазон
измерений
— это
та часть диапазона показаний прибора,
для которой усыновлены погрешности
прибора (если известны погрешности
прибора, то диапазон измерений и показаний
прибора совпадает).

Разность
между
максимальным и минимальным показаниями
прибора называют
размахом.

Другой
характеристикой прибора является его
чувствительность,
т.
е. способность отсчитывающего устройства
реагировать на изменения измеряемой
величины. Под порогом чувствительности
прибора понимают наи­меньшее значение
измеряемой величины, вызывающее изменение
показания прибора, которое можно
зафиксировать.

Основной
характеристикой прибора является его
точность.
Она
характеризуется суммарной погрешностью.

Средства
измерения делятся на классы точности.
Класс
точности —
это
обобщенная характеристика, определяемая
пределами основной и дополнительных
допускаемых погрешностей, влияющих на
точность.

Стабильность
(воспроизводимость
прибора) — это свойство отсчетного
устройства
обеспечивать
постоянство показаний одной и той же
величины.

Все
средства измерения (приборы, используемые
для измерения в научных исследованиях)
проходят
периодическую
поверку
на
точность. Такая поверка предусматривает
определение и по возможности уменьшение
погрешностей приборов. Поверка позволяет
установить соответствие данного прибора
регламентированной степени точности
и определяет возможность его применения
для данных измерений, т. е. определяются
погрешности и устанавливается, не
выхолят ли они за пределы допускаемых
значении. Поверку средств измерений
производят на различных уровнях.

Государственные
метрологические институты и лаборатории
по надзору за стандартами и измерительной
техникой производят государственный
контроль за
обеспечением в стране единства мер.

В
периоды между государственными поверками
осуществляется ведомственная
поверка средств
измерений, которая по объему работ мало
чем от­личается от государственных
поверок. Такие поверки более оперативны
и про­водятся по специальному графику,
разработанному для данной организации.

Рабочая
поверка средств
измерений проводится в низовых звеньях
каждым экспериментатором непосредственно
в организациях перед началом из­мерений
и наблюдений.

Под
регулировкой
прибора понимают
операции, направленные на снижение
систематических ошибок до величины,
меньшей допустимой погрешности.

С.-Петербург — 1992 г. ГСИ. Погрешности измерений. Обозначения МИ 2246-93 Рекомендация распространяется на нормативную документацию (далее — НД) и устанавливает обозначения погрешностей измерений величин.1.1 Погрешность измерений — отклонение результата измерений от действительного значения измеряемой величины — может состоять из инструментальной погрешности, погрешности метода, погрешности оператора и др.

погрешностей. Погрешность измерений и ее составляющие представлены на схеме в приложении 1.1.2 Погрешность измерений при воспроизведении единицы величины называют погрешностью воспроизведения единицы, а при передаче размера единицы величины называют погрешностью передачи размера единицы величины или погрешностью поверки (погрешностью аттестации).1.3 Погрешности измерений подразделяют: в зависимости от характера проявления на систематические, случайные; в зависимости от характера их изменения в диапазоне измеряемой величины на аддитивные и мультипликативные; по форме представления на абсолютные и относительные.1.4 Погрешность измерений может быть выражена в виде: доверительного интервала; пределов допускаемой погрешности; характеристик распределения погрешностей (среднее квадратическое отклонение результата измерений, размах, среднее арифметическое и др.

характеристики). Примечание. Задаваемые или допускаемые характеристики погрешностей измерений могут быть выражены в соответствии с требованиями, установленными в МИ 1317, в форме: предела допускаемых значений характеристики; нижнего и верхнего пределов допускаемых значений характеристики.1.5 Наибольший вклад в погрешность измерений, как правило, вносит инструментальная погрешность, обусловленная погрешностью применяемого средства измерений (далее — СИ).

Инструментальная погрешность и ее составляющие приведены в приложении 2.2.1 Для обозначения какой-либо погрешности используют букву греческого алфавита «дельта» — Δ (прописная), δ (строчная). Прописной буквой Δ обозначают абсолютную погрешность измерения и строчной буквой δ — относительную погрешность измерения.2.2 Неисключенную систематическую погрешность измерения рекомендуется обозначать буквой греческого алфавита «тэта» — Θ.2.3.

Среднее квадратическое отклонение и размах — характеристики случайной погрешности — рекомендуется обозначать буквами латинского алфавита S и R соответственно.2.4. Поправку, которую вводят в неисправленный результат измерения с целью исключения одной или нескольких систематических погрешностей, обозначают символом Ñ (перевернутой буквой греческого алфавита «дельта»).2.5 Метрологические характеристики СИ — нестабильность и вариацию — рекомендуется обозначать буквой греческого v (ню) и латинского V алфавитов соответственно.3.1 При необходимости конкретизации погрешности измерения (указания ее составляющей, формы представления или внесения других уточняющих данных) рекомендуется символ погрешности сопровождать индексом (индексами).3.2 В качестве индексов используют первую букву или несколько букв того слова, которое определяет или источник погрешности, или форму представления ее, или другие особенности погрешности.

Какой буквой погрешность?

2.1 Для обозначения какой-либо погрешности используют букву греческого алфавита ‘дельта’ — Д (прописная), 5 (строчная). Прописной буквой Д обозначают абсолютную погрешность измерения и строчной буквой 8 — относительную погрешность измерения.

Каким символом обозначается погрешность?

Для обозначения абсолютной погрешности числа x будем использовать символ ∆x.

Как в физике обозначается погрешность?

Результаты измерения записывают в виде A = a ± Δ a, где A — измеряемая величина, a — средний результат полученных измерений, Δ a — абсолютная погрешность измерений.

Как определить погрешность?

По форме представления — Первый тип — абсолютная погрешность. Она представляет собой алгебраическую разность между реальным и номинальными значениями. Она регистрируется в тех же величинах, что и основной объект. В расчетах абсолютный показатель помечается буквой ∆.

• Например, линейка — наиболее простой и привычный каждому измерительный инструмент.
• При помощи верхней шкалы на ней определяются значения с точностью до миллиметра.
• Нижняя имеет другой масштаб (до 0,1 дюйма–2,54 мм).
• Несложно проверить, что на этом приборе погрешность верхней части меньше, чем нижней.
• Точность измерений в случае с линейкой будет зависеть от ее конструктивных особенностей.

Абсолютная погрешность измеряется той же единицей измерений, что и изучаемая величина. В процессе используется формула: Δ = х1 – х2, где х1 — измеренная величина, а х2 — реальная величина. Второй тип – относительная погрешность (проявляется в виде отношение абсолютного и истинного значения).

Показатель не имеет собственной единица измерения или отражается процентно. В расчетах помечается как δ. Она является более сложным значением, чем может показаться. В расчетах используется формула: δ = (Δ / х2)·100 % Стоит отметить, что если истинное значение имеет малую величину, то относительная — большую.

Например, если стандартной линейкой (30 см) измеряется коробки (150 мм), то вычисление будет иметь вид: δ = 1 мм/150 мм = 0,66%. Если этот же прибор использовать для экрана смартфона (80 мм), то получится δ = 1 мм/80 мм = 1,25%. Получается, что в обоих случаях абсолютная погрешность не изменяется, но относительная отличается в разы.

• Во втором случае рекомендуется использовать более точный прибор.
• Последний тип — приведенная погрешность.
• Она используется, чтобы не допустить такого разброса на одном приборе.
• Работает, как относительная, но вместо истинного значения в формуле применяется нормирующая шкала (общая длина линейки, например).

γ = (Δ / х3)·100 %, где х3 — это нормирующая шкала Например, если потребуется измерить ту же коробку и смартфон, то придется учесть абсолютную величину в 1мм и приведенную погрешность — 1/300*100 =0,33 %. Если взять швейный метр и сравнить его с линейкой, то получится, что первый показатель в обоих случаях остается 1 мм, а второй отличается в разы (0,33% и 0,1%).

Как найти погрешность в математике?

Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом: Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.

Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения. Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см.

Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Как найти погрешность измерений формула?

Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).

В чем измеряется погрешность?

Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины. Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.

Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.

1. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается.
2. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
3. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.

Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

В чем измеряется приведенная погрешность?

Приведенную погрешность обычно выражают в процентах.

Что такое погрешность и виды?

Абсолютная погрешность меры — это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины. Относительная погрешность — это число, отражающее степень точности измерения.

Как правильно записать результат с погрешностью?

1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной, — если первая есть 3 и более.2. Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.

Чему равна абсолютная погрешность?

При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения.

Что такое точность в физике?

То́чность измере́ний, точность результата измерения — близость измеренного значения к истинному значению измеряемой величины, Точность измерений описывает качество измерений в целом, объединяя понятия правильность измерений и прецизионность измерений,

Как определить цену деления и погрешность?

Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков.

Какие существуют погрешности?

Абсолютная погрешность измерения — разность между значением величины, полученным при измерении, и ее истинным значением, выражаемая в единицах измеряемой величины. Относительная погрешность измерения — отношение абсолютной погрешности, измерения к истинному значению измеряемой величины.

Чему равен класс точности?

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 мая 2018 года; проверки требуют 13 правок, Класс точности — обобщённая характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений.

результату измерения (по относительной погрешности)

в этом случае, по ГОСТ 8.401-80, цифровое обозначение класса точности (в процентах) заключается в кружок.

длине (верхнему пределу) шкалы измерительного прибора (по приведенной погрешности).

Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора.

Так, для вольтметра, работающего в диапазоне измерений 0—30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений.

При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1—0,5 В. Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора.

• Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления.
• Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.
• Следует иметь в виду, что понятие класса точности встречается в различных областях техники.

Так, в станкостроении имеется понятие класса точности металлорежущего станка, класса точности электроэрозионных станков (по ГОСТ 20551). Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков.

Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений.

Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.

В чем измеряется погрешность?

Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

1. Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
2. Инструментальные и методические погрешности.
3. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
4. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.

Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.

• Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается.
• Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
• Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.

Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Какой буквой обозначается класс точности?

Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей в соответствии с формулой δ = ±, классы точности в документации обозначаются числами с и d, разделенных косой чертой.

Как классифицируется погрешность?

Погрешности измерений классифицируются по следующим признакам. По способу математического выражения погрешности делятся на абсолютные погрешности и относительные погрешности. По взаимодействию изменений во времени и входной величины погрешности делятся на статические погрешности и динамические погрешности.

Что такое погрешность в математике?

Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения. Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного.

Это отклонение принято называть ошибкой измерения, Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов, На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,

Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность,

1. Например, запись T = 2,8 ± 0,1 с; P = 0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95 %.
2. Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как « неопределённость измерения ».

В то же время иногда, особенно в физике, термин «погрешность измерения» ( англ. measurement error ) используется как синоним термина «неопределённость измерения» ( англ. measurement uncertainty ),

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

• Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°